6.4: Ортогональні набори
- Page ID
- 62915
- Зрозумійте, який найкращий метод для обчислення ортогональної проекції в даній ситуації.
- Рецепти: ортонормальний набір з ортогональної множини, Формула проекції, B-координати, коли B є ортогональною множиною, процес Грам—Шмідта.
- Словникові слова: ортогональна множина, ортонормальна множина.
У цьому розділі ми наведемо формулу ортогональної проекції, яка значно простіша, ніж у Розділі 6.3, оскільки вона не вимагає зменшення рядків або інверсії матриці. Однак ця формула, звана Формулою проекції, працює тільки при наявності ортогональної основи. Ми також представимо процес Грам—Шмідта для перетворення довільної основи в ортогональну.
Ортогональні множини та формула проекції
Обчислення за участю проекцій, як правило, набагато простіше при наявності ортогонального набору векторів.
Набір ненульових векторів\(\{u_1,\: u_2,\cdots ,u_m\}\) називається ортогональним, якщо\(u_i\cdot u_j=0\) щоразу\(i\neq j\). Вона ортонормальна, якщо вона ортогональна, і\(u_i\cdot u_i=1\) на додаток для всіх\(i=1,\: 2,\cdots ,m\).
Іншими словами, набір векторів ортогональний, якщо різні вектори в множині перпендикулярні один одному. Ортонормальна множина - це ортогональний набір одиничних векторів, визначення 6.1.3 в розділі 6.1.
Стандартні вектори координат\(\mathbb{R}^n\) завжди утворюють ортонормальну множину. Наприклад, в\(\mathbb{R}^3\) ми перевіряємо, що
\[\left(\begin{array}{c}1\\0\\0\end{array}\right)\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)=0\quad\left(\begin{array}{c}1\\0\\0\end{array}\right)\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)=0\quad\left(\begin{array}{c}0\\1\\0\end{array}\right)\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)=0.\nonumber\]
Оскільки\(e_i\cdot e_i=1\) для всіх це показує\(i=1,\: 2,\:3\), що\(\{e_1,\: e_2,\: e_3\}\) є ортонормальним.
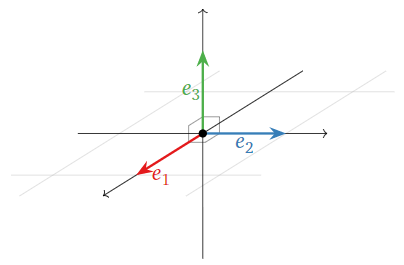
Малюнок\(\PageIndex{1}\)
Чи є цей набір ортогональним? Це ортонормально?
\[\mathcal{B}=\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\left(\begin{array}{c}1\\-2\\1\end{array}\right),\left(\begin{array}{c}1\\0\\-1\end{array}\right)\right\}\nonumber\]
Рішення
Перевіряємо, що
\[\left(\begin{array}{c}1\\1\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\-2\\1\end{array}\right)=0\quad\left(\begin{array}{c}1\\1\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\0\\-1\end{array}\right)=0\quad\left(\begin{array}{c}1\\-2\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\0\\-1\end{array}\right)=0.\nonumber\]
Тому\(\mathcal{B}\) є ортогональним.
Малюнок\(\PageIndex{2}\)
Набір не\(\mathcal{B}\) є ортонормальним, оскільки, наприклад,
\[\left(\begin{array}{c}1\\1\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\1\end{array}\right)=3\neq 1.\nonumber\]
Однак ми можемо зробити його ортонормальним, замінивши кожен вектор на одиничний вектор у напрямку, Факт 6.1.3 в розділі 6.1, кожен вектор:
\[\left\{\frac{1}{\sqrt{3}}\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\frac{1}{\sqrt{6}}\left(\begin{array}{c}1\\-2\\1\end{array}\right),\:\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\0\\-1\end{array}\right)\right\}\nonumber\]
є ортонормальним.
У попередньому прикладі ми бачили, що легко створити ортонормальний набір векторів з ортогонального шляхом заміни кожного вектора на одиничний вектор в тому ж напрямку.
Якщо\(\{v_1,\: v_2,\cdots ,v_m\}\) є ортогональним набором векторів, то
\[\left\{\frac{v_1}{||v_1||},\:\frac{v_2}{||v_2||},\cdots ,\frac{v_m}{||v_m||}\right\}\nonumber\]
є ортонормальним набором.
\(a,\:b\)Дозволяти скаляри, і нехай
\[u_1=\left(\begin{array}{c}a\\b\end{array}\right)\quad u_2=\left(\begin{array}{c}-b\\a\end{array}\right).\nonumber\]
\(\mathcal{B}=\{u_1,\: u_2\}\)Ортогональний?
Рішення
Нам залишається лише перевірити, що
\[\left(\begin{array}{c}a\\b\end{array}\right)\cdot\left(\begin{array}{c}-b\\a\end{array}\right)=-ab+ab=0.\nonumber\]
Тому\(\{u_1,\:u_2\}\) ортогональний, хіба що\(a=b=0\).
Чи є цей набір ортогональним?
\[\mathcal{B}=\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\left(\begin{array}{c}1\\-2\\1\end{array}\right),\:\left(\begin{array}{c}1\\-1\\-1\end{array}\right)\right\}\nonumber\]
Рішення
Цей набір не є ортогональним, оскільки
\[\left(\begin{array}{c}1\\1\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\-1\\-1\end{array}\right)=1-1-1=-1\neq 0.\nonumber\]
Ми побачимо, як створити ортогональний набір з\(\mathcal{B}\) підрозділу: Процес Грама-Шмідта.
Приємна властивість, якою користуються ортогональні набори, полягає в тому, що вони автоматично лінійно незалежні.
Ортогональний набір лінійно незалежний. Тому вона є основою для його прольоту.
- Доказ
-
Припустимо, що\(\{u_1,\: u_2,\cdots ,u_m\}\) є ортогональним. Потрібно показати, що рівняння
\[c_1u_1+c_2u_2+\cdots +c_mu_m=0\nonumber\]
має лише тривіальне рішення\(c_1=c_2=\cdots =c_m=0\). Прийняття точкового добутку обох сторін цього рівняння з u1 дає
\[\begin{aligned} 0=u_1\cdot 0&=u_1\cdot(c_1u_1+c_2u_2+\cdots +c_mu_m) \\ &=c_1(u_1\cdot u_1)+c_2(u_1\cdot u_2)+\cdots +c_m(u_1\cdot u_m) \\ &=c_1(u_1\cdot u_1)\end{aligned}\]
тому що\(u_1\cdot u_i=0\) для\(i>1\). Так як у\(u\neq 0\) нас\(u_1\cdot u_1\neq 0\), так\(c_1=0\). Аналогічно, взявши точковий добуток з\(u_i\) показує\(c_i=0\), що кожен, за бажанням.
Однією з переваг роботи з ортогональними множинами є те, що вона дає просту формулу для ортогональної проекції, визначення 6.3.2 в розділі 6.3, вектора.
\(W\)Дозволяти підпростір\(\mathbb{R}^n\), і нехай\(\{u_1,\:u_2,\cdots ,u_m\}\) бути ортогональною основою для\(W\). Тоді для будь-якого вектора\(x\)\(\mathbb{R}^n\) in ортогональна проекція\(x\) onto\(W\) задається формулою
\[x_{W}=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\cdots +\frac{x\cdot u_m}{u_m\cdot u_m}u_m.\nonumber\]
- Доказ
-
Нехай
\[y=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\cdots +\frac{x\cdot u_m}{u_m\cdot u_m}u_m.\nonumber\]
Цей вектор міститься в\(W\) тому, що він являє собою лінійну комбінацію\(u_1,\: u_2,\cdots ,u_m\). Отже, нам просто потрібно показати, що\(x−y\) є в\(W^{\perp}\), тобто, що\(u_i\cdot (x−y)=0\) для кожного\(i=1,\: 2,\cdots ,m\). Бо\(u_1\), у нас є
\[\begin{aligned}u_1\cdot (x-y)&=u_1\cdot\left(x-\frac{x\cdot u_1}{u_1\cdot u_1}u_1-\frac{x\cdot u_2}{u_2\cdot u_2}u_2-\cdots -\frac{x\cdot u_m}{u_m\cdot u_m}u_m\right) \\ &=u_1\cdot x-\frac{x\cdot u_1}{u_1\cdot u_1}(u_1\cdot u_1)-0-\cdots -0 \\ &=0.\end{aligned}\]
Подібний розрахунок показує, що\(u_i\cdot (x−y)=0\) для кожного\(i\), так\(x−y\) є в\(W^{\perp}\), за бажанням.
Якщо\(\{u_1,\: u_2,\cdots ,u_m\}\) є орто нормальною основою для\(W\), то знаменники\(u_i\cdot u_i=1\) йдуть, тому формула проекції стає ще простіше:
\[x_{W}=(x\cdot u_1)u_1+(x\cdot u_2)u_2+\cdots +(x\cdot u_m)u_m.\nonumber\]
Припустимо, що\(L=\text{Span}\{u\}\) це лінія. Набір\(\{u\}\) є ортогональною основою для\(L\), тому Формула проекції говорить, що для будь-якого вектора\(x\) ми маємо
\[x_{L}=\frac{x\cdot u}{u\cdot u}u,\nonumber\]
як у прикладі 6.3.7 в розділі 6.3. Див. також Приклад 6.3.8 у розділі 6.3 та приклад 6.3.9 у розділі 6.3.
Припустимо, що\(\{u_1,\: u_2,\cdots ,u_m\}\) це ортогональна основа для підпростору\(W\), і нехай\(L_i=\text{Span}\{u_i\}\) для кожного\(i=1,\: 2,\cdots ,m\). Тоді ми бачимо, що для будь-якого вектора х, у нас є
\[\begin{aligned}x_{W}&=\frac{x\cdot u_1}{u_1\cdot u_1}u_2+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\cdots +\frac{x\cdot u_m}{u_m\cdot u_m}u_m \\ &=x_{L_{1}}+x_{L_{2}}+\cdots+x_{L_{m}}\end{aligned}\]
Іншими словами, для ортогональної основи проекція\(x\) onto\(W\) - це сума проекцій на лінії, що охоплюються базисними векторами. У цьому сенсі проекція на лінію є найважливішим прикладом ортогональної проекції.
Продовжуючи приклад 6.3.1 у розділі 6.3 та прикладі 6.3.10 у розділі 6.3, використовуйте формулу проекції, Теорема\(\PageIndex{1}\) для обчислення ортогональної проекції вектора на\(xy\) площину -в\(\mathbb{R}^{3}\).
Рішення
Базис для\(xy\) -площини задається двома стандартними векторами координат
\[e_1=\left(\begin{array}{c}1\\0\\0\end{array}\right)\quad e_2=\left(\begin{array}{c}0\\1\\0\end{array}\right).\nonumber\]
Набір\(\{e_1,\:e_2\}\) ортогональний, так що для будь-якого вектора\(x=(x_1,\:x_2,\:x_3)\), у нас є
\[x_{W}=\frac{x\cdot e_1}{e_1\cdot e_1}e_1+\frac{x\cdot e_2}{e_2\cdot e_2}e_2=x_1e_1+x_2e_2=\left(\begin{array}{c}x_1\\x_2\\0\end{array}\right).\nonumber\]
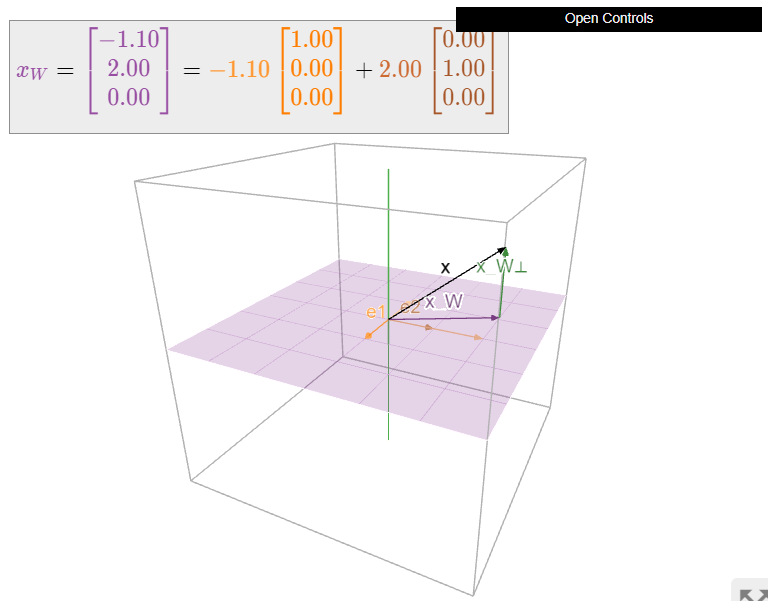
Рисунок\(\PageIndex{3}\): Ортогональна проекція вектора на\(xy\) -площину в\(\mathbb{R}^3\). Зверніть увагу, що\(x_{W}\) це сума проекцій\(x\) на осі\(e_1\) - і\(e_2\) -координат (показані помаранчевим і коричневим кольором відповідно).
Нехай
\[W=\text{Span}\left\{\left(\begin{array}{c}1\\0\\-1\end{array}\right),\left(\begin{array}{c}1\\1\\1\end{array}\right)\right\}\quad x=\left(\begin{array}{c}2\\3\\-2\end{array}\right).\nonumber\]
Знайти\(x_{W}\) і\(x_{W^{\perp}}\).
Рішення
Вектори
\[u_1=\left(\begin{array}{c}1\\0\\-1\end{array}\right)\quad u_2=\left(\begin{array}{c}1\\1\\1\end{array}\right)\nonumber\]
ортогональні, тому ми можемо використовувати формулу проекції:
\[x_{W}=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2=\frac{4}{2}\left(\begin{array}{c}1\\0\\-1\end{array}\right)+\frac{3}{3}\left(\begin{array}{c}1\\1\\1\end{array}\right)=\left(\begin{array}{c}3\\1\\-1\end{array}\right).\nonumber\]
Тоді у нас є
\[x_{W^{\perp}}=x-x_{W}=\left(\begin{array}{c}-1\\2\\-1\end{array}\right).\nonumber\]
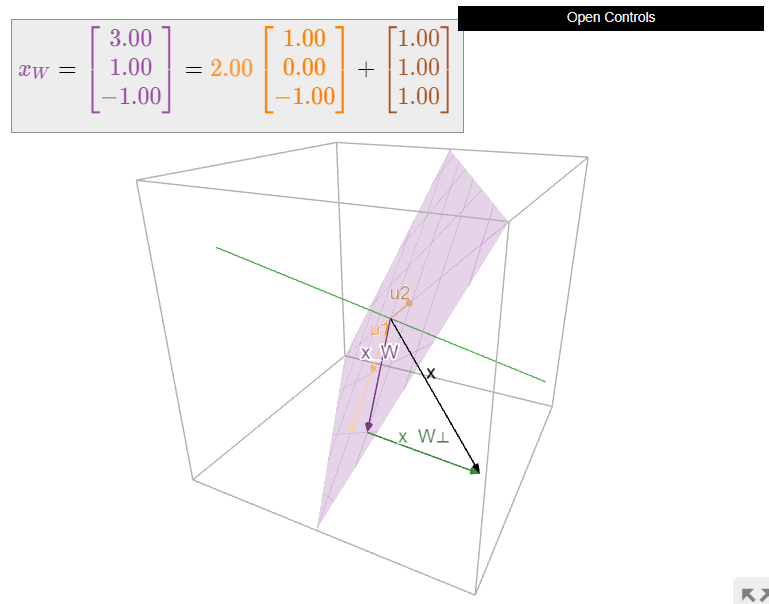
Рисунок\(\PageIndex{4}\): Ортогональна проекція вектора на площину\(W\). Зверніть увагу, що\(x_W\) це сума проекцій\(x\) на лінії, що охоплюються\(u_1\) і\(u_2\) (показані помаранчевим і коричневим, відповідно).
Нехай
\[W=\text{Span}\left\{\left(\begin{array}{c}1\\0\\-1\\0\end{array}\right),\left(\begin{array}{c}0\\1\\0\\-1\end{array}\right),\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)\right\}\quad x=\left(\begin{array}{c}0\\1\\3\\4\end{array}\right).\nonumber\]
Обчислити\(x_{W}\), і знайти відстань від\(x\) до\(W\).
Рішення
Вектори
\[u_1=\left(\begin{array}{c}1\\0\\-1\\0\end{array}\right)\quad u_2=\left(\begin{array}{c}0\\1\\0\\-1\end{array}\right)\quad u_3=\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)\nonumber\]
ортогональні, тому ми можемо використовувати формулу проекції:
\[\begin{aligned} x_{W}&=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\frac{x\dot u_3}{u_3\cdot u_3}u_3 \\ &=\frac{-3}{2}\left(\begin{array}{c}1\\0\\-1\\0\end{array}\right)+\frac{-3}{2}\left(\begin{array}{c}0\\1\\0\\-1\end{array}\right)+\frac{8}{4}\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)=\frac{1}{2}\left(\begin{array}{c}1\\1\\7\\7\end{array}\right) \\ x_{W^{\perp}}&=x-x_{W}=\frac{1}{2}\left(\begin{array}{c}-1\\1\\-1\\1\end{array}\right).\end{aligned}\]
Відстань від\(x\)\(W\) до
\[||x_{W^{\perp}}||=\frac{1}{2}\sqrt{1+1+1+1}=1.\nonumber\]
Тепер нехай\(W\) буде підпростір\(\mathbb{R}^n\) з ортогональної основи\(\mathcal{B}=\{v_1,\: v_2,\cdots ,v_m\}\), і нехай\(x\) бути вектор в\(W\). Потім\(x=x_{W}\), так за формулою проекції, Теорема\(\PageIndex{1}\), у нас є
\[x=x_{W}=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\cdots +\frac{x\cdot u_m}{u_m\cdot u_m}u_m.\nonumber\]
Це дає нам спосіб вираження\(x\) як лінійну комбінацію базисних векторів у\(\mathcal{B}\): ми обчислили\(\mathcal{B}\) -координати, визначення 2.8.1 в розділі 2.8, або\(x\) без зменшення рядка!
\(W\)Дозволяти підпростір\(\mathbb{R}^n\) з ортогональної основи\(\mathcal{B}=\{v_1,\: v_2,\cdots ,v_m\}\) і нехай\(x\) бути вектор в\(W\). Тоді
\[[x]_{\mathcal{B}}=\left(\frac{x\cdot u_1}{u_1\cdot u_1},\:\frac{x\cdot u_2}{u_2\cdot u_2},\cdots ,\frac{x\cdot u_m}{u_m\cdot u_m}\right).\nonumber\]
Як і при ортогональних проекціях, якщо\(\{u_1,\: u_2,\cdots ,u_m\}\) є орто нормальною основою\(W\), то формула ще простіше:
\[[x]_{\mathcal{B}}=\left(x\cdot u_1,\: x\cdot u_2,\cdots ,x\cdot u_m\right).\nonumber\]
Знайти\(\mathcal{B}\) -координати\(x\), де
\[\mathcal{B}=\left\{\left(\begin{array}{c}1\\2\end{array}\right),\left(\begin{array}{c}-4\\2\end{array}\right)\right\}\quad x=\left(\begin{array}{c}0\\3\end{array}\right).\nonumber\]
Рішення
Так як
\[u_1=\left(\begin{array}{c}1\\2\end{array}\right)\quad u_2=\left(\begin{array}{c}-4\\2\end{array}\right)\nonumber\]
утворюють ортогональну основу\(\mathbb{R}^2\), ми маємо
\[[x]_{\mathcal{B}}=\left(\frac{x\cdot u_1}{u_1\cdot u_1},\frac{x\cdot u_2}{u_2\cdot u_2}\right)=\left(\frac{3\cdot 2}{1^2+2^2},\frac{3\cdot 2}{(-4)^2+2^2}\right)=\left(\frac{6}{5},\frac{3}{10}\right).\nonumber\]
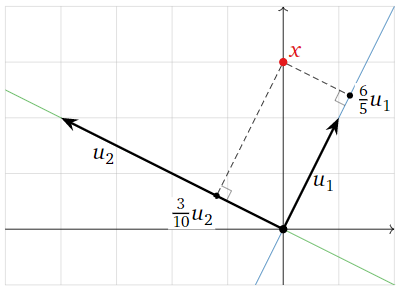
Малюнок\(\PageIndex{5}\)
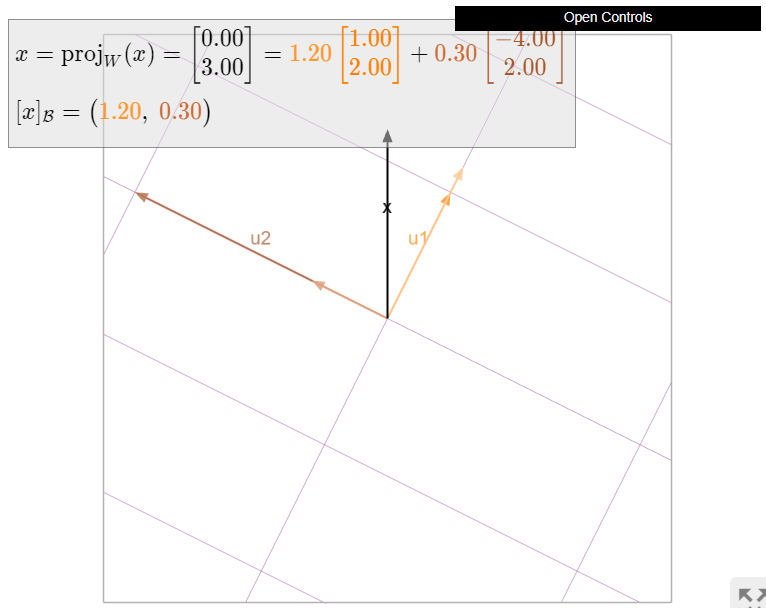
Малюнок\(\PageIndex{6}\): Обчислення\(\mathcal{B}\) -координат за формулою проекції.
Наступний приклад показує, що формула проекції насправді вимагає ортогональної основи.
Розглянемо\(\mathcal{B}=\{v_1,\: v_2\}\) основу\(\mathbb{R}^2\), де
\[v_1=\left(\begin{array}{c}2\\-1/2\end{array}\right)\quad v_2=\left(\begin{array}{c}1\\2\end{array}\right).\nonumber\]
Це не ортогонально, тому що\(v_1\cdot v_2=2−1=1\neq 0\). Нехай\(x=\left(\begin{array}{c}1\\1\end{array}\right)\). Спробуємо провести обчислення\(x=x_{\mathbb{R}^{2}}\) за формулою проекції щодо основи\(\mathcal{B}\):
\[x_{\mathbb{R}^{2}}=\color{Green}{\frac{x\cdot v_1}{v_1\cdot v_1}v_1}\color{black}{+}\color{Purple}{\frac{x\cdot v_2}{v_2\cdot v_2}v_2}\color{black}{=}\color{Green}{\frac{3/2}{17/4}\left(\begin{array}{c}2\\-1/2\end{array}\right)}\color{black}{+}\color{Purple}{\frac{3}{5}\left(\begin{array}{c}1\\2\end{array}\right)}\color{black}{=\left(\begin{array}{c}111/85\\ 87/85\end{array}\right)\neq x.}\nonumber\]
Оскільки ми бачимо\(x=x_{\mathbb{R}^{2}}\), що Формула проекції не обчислює ортогональну проекцію в даному випадку. Геометрично проекції\(x\) на лінії натягнуті\(v_1\) і\(v_2\) не сумуються\(x\), як ми бачимо з малюнка.
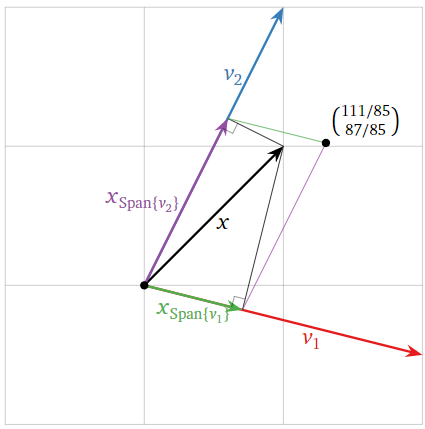
Малюнок\(\PageIndex{7}\)
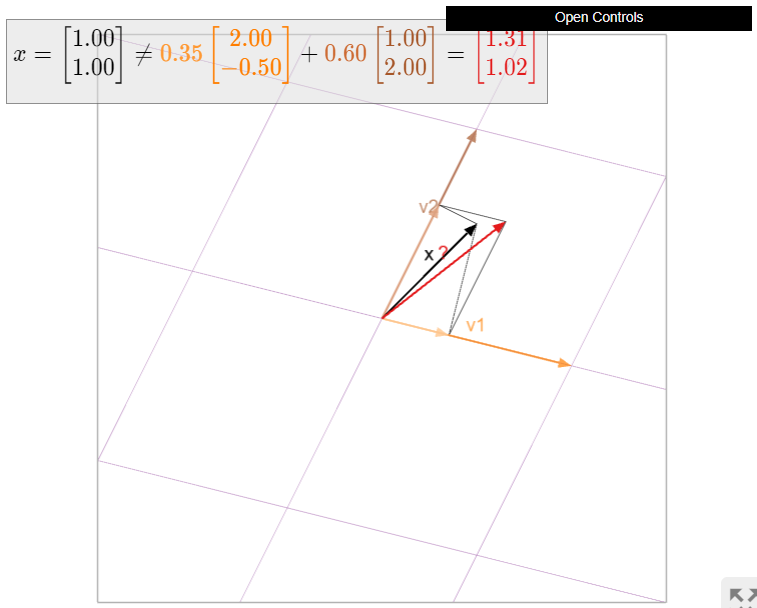
Малюнок\(\PageIndex{8}\): Коли\(v_1\) і\(v_2\) не ортогональні, то\(x_{\mathbb{R}^{2}}=x\) не обов'язково дорівнює сумі (червоний) проекцій (помаранчевий і коричневий)\(x\) на лінії, що охоплюються\(v_1\) і\(v_2\).
Для використання формули проекції потрібна ортогональна основа.
Процес Грама-Шмідта
Ми бачили в попередньому підрозділі, що ортогональні проекції та\(\mathcal{B}\) -координати набагато простіше обчислити при наявності ортогональної основи для підпростору. У цьому підрозділі наведено метод, який називається процесом Грам—Шмідта, для обчислення ортогональної основи підпростору.
\(v_1,\: v_2,\cdots ,v_m\)Дозволяти бути основою для\(W\) підпростору\(\mathbb{R}^{n}\). Визначте:
- \(u_1=v_1\)
- \(u_2=(v_2)_{\text{Span}\{u_1\}^{\perp}}\qquad\qquad =v_2-\frac{v_2\cdot u_1}{u_1\cdot u_1}u_1\)
- \(u_3=(v_3)_{\text{Span}\{u_1,u_2\}^{\perp}}\qquad\quad\; =v_3-\frac{v_3\cdot u_1}{u_1\cdot u_1}u_1-\frac{v_3\cdot u_2}{u_2\cdot u_2}u_2\)
\(\quad\vdots\)
- \(u_m=(v_m)_{\text{Span}\{u_1,u_2,\cdots ,u_{m-1}\}^{\perp}}=v_m-\sum\limits_{i=1}^{m-1}\frac{v_m\cdot u_i}{u_i\cdot u_i}u_i\).
Потім\(\{u_1,\: u_2,\cdots ,u_m\}\) - ортогональна основа для того ж підпростору\(W\).
- Доказ
-
Спочатку ми стверджуємо, що кожен\(u_i\) знаходиться в\(W\), і насправді, що\(u_i\) знаходиться в\(\text{Span}\{v_1,\: v_2,\cdots ,v_i\}\). Ясно\(u_1=v_1\), що в\(\text{Span}\{v_1\}\). Потім\(u_2\) лінійна комбінація\(u_1\) і\(v_2\), які обидва в\(\text{Span}\{v_1,\: v_2\}\),\(u_2\) так і в\(\text{Span}\{v_1,\:v_2\}\). Аналогічно,\(u_3\) це лінійна комбінація\(u_1,\: u_2\)\(v_3\), і, які всі в\(\text{Span}\{v_1,\: v_2,\: v_3\}\), так\(u_3\) є в\(\text{Span}\{v_1,\: v_2,\: v_3\}\). Продовжуючи таким чином, ми бачимо, що кожен\(u_i\) знаходиться в\(\text{Span}\{v_1,\: v_2,\cdots ,v_i\}\).
Тепер ми стверджуємо, що\(\{u_1,\: u_2,\cdots ,u_m\}\) це ортогональний набір. Нехай\(1\leq i < j\leq m\). Потім\(u_j=(v_j)_{\text{Span}\{u_1,\:u_2,\cdots ,u_{j−1}\}^{\perp}}\), так за визначенням\(u_j\) є ортогональним до кожного вектора в\(\text{Span}\{u_1,\:u_2,\cdots ,u_{j−1}\}\). Зокрема,\(u_j\) є ортогональним до\(u_i\).
Нам ще належить довести, що кожен з них\(u_i\) ненульовий. Чітко\(u_1=v_1\neq 0\). Припустимо, що\(u_i=0\). Тоді\((v_i)_{\text{Span}\{u_1,\:u_2,\cdots,u_{i−1}\}^{\perp}}=0\), що означає, що\(v_i\) знаходиться в\(\text{Span}\{u_1,\:u_2,\cdots ,u_{i−1}\}\). Але кожен\(u_1,\: u_2,\cdots ,u_{i−1}\) знаходиться в\(\text{Span}\{v_1,\:v_2,\cdots ,v_{i−1}\}\) першому пункті,\(v_i\) так і в\(\text{Span}\{v_1,\: v_2,\cdots ,v_{i−1}\}\). Це суперечить зростаючому критерію прольоту теореми 2.5.2 у розділі 2.5; отже,\(u_i\) має бути ненульовим.
Попередні два абзаци виправдовують використання формули проекції, Теорема\(\PageIndex{1}\), в рівності
\[(v_i)_{\text{Span}\{u_1,\:u_2,\cdots ,u_{i-1}\}^{\perp}}=v_i-(v_i)_{\text{Span}\{u_1,\:u_2,\cdots ,u_{i-1}\}}=v_i-\sum\limits_{j=1}^{i-1}\frac{v_i\cdot u_j}{u_j\cdot u_j}u_j\nonumber\]
в постановці теореми.
Оскільки\(\{u_1,\: u_2,\cdots ,u_m\}\) є ортогональним набором, він лінійно незалежний. Таким чином, це набір\(m\) лінійно незалежних векторів в\(W\), тому він є\(W\) основою для теореми основи, Теорема 2.7.3 в розділі 2.7. Аналогічно, для кожного\(i\), ми бачили, що\(\{u_1,\: u_2,\cdots ,u_i\}\) множина міститься в\(i\) -вимірному підпросторі\(\text{Span}\{v_1,\:v_2,\cdots ,v_i\}\), тому\(\{u_1,\:u_2,\cdots ,u_i\}\) є ортогональною основою для\(\text{Span}\{v_1,\:v_2,\cdots ,v_i\}\).
Знайти ортогональну основу\(\{u_1,\:u_2\}\) для\(W=\text{Span}\{v_1,\:v_2\}\), де
\[v_1=\left(\begin{array}{c}1\\1\\0\end{array}\right)\quad v_2=\left(\begin{array}{c}1\\1\\1\end{array}\right).\nonumber\]
Рішення
Біжимо Грам—Шмідта: спочатку беремо\(u_1=v_1\), потім
\[u_2=v_2-\frac{v_2\cdot u_1}{u_1\cdot u_1}u_1=\left(\begin{array}{c}1\\1\\1\end{array}\right)-\frac{2}{2}\left(\begin{array}{c}1\\1\\0\end{array}\right)=\left(\begin{array}{c}0\\0\\1\end{array}\right).\nonumber\]
Тоді\(\{u_1,\:u_2\}\) ортогональна основа для\(W\): дійсно, зрозуміло, що\(u_1\cdot u_2=0\).
Геометрично ми просто замінюємо на\(v_2\) ту частину\(v_2\), яка перпендикулярна лінії\(L_1=\text{Span}\{v_1\}\):
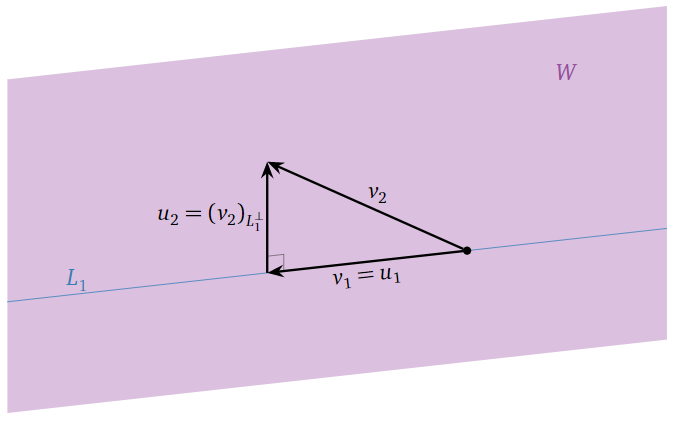
Малюнок\(\PageIndex{9}\)
Знайти ортогональну основу\(\{u_1,\: u_2,\:u_3\}\) для\(W=\text{Span}\{v_1,\:v_2,\:v_3\}=\mathbb{R}^3\), де
\[v_1=\left(\begin{array}{c}1\\1\\0\end{array}\right)\quad v_2=\left(\begin{array}{c}1\\1\\1\end{array}\right)\quad v_3=\left(\begin{array}{c}3\\1\\1\end{array}\right).\nonumber\]
Рішення
Запускаємо Грам-Шмідта:
- \(u_1=v_1=\left(\begin{array}{c}1\\1\\0\end{array}\right)\)
- \(u_2=v_2=\frac{v_2\cdot u_1}{u_1\cdot u_1}u_1=\left(\begin{array}{c}1\\1\\1\end{array}\right)-\frac{2}{2}\left(\begin{array}{c}1\\1\\0\end{array}\right)=\left(\begin{array}{c}0\\0\\1\end{array}\right)\)
- \(\begin{aligned}u_3&=v_3-\frac{v_3\cdot u_1}{u_1\cdot u_1}u_1-\frac{v_3\cdot u_2}{u_2\cdot u_2}u_2 \\ &=\left(\begin{array}{c}3\\1\\1\end{array}\right)-\frac{4}{2}\left(\begin{array}{c}1\\1\\0\end{array}\right)-\frac{1}{1}\left(\begin{array}{c}0\\0\\1\end{array}\right)=\left(\begin{array}{c}1\\-1\\0\end{array}\right).\end{aligned}\)
Тоді\(\{u_1,\:u_2,\:u_3\}\) ортогональна основа для\(W\): дійсно, ми маємо
\[u_1\cdot u_2=0\quad u_1\cdot u_3=0\quad u_2\cdot u_3=0.\nonumber\]
Геометрично, як тільки ми маємо\(u_1\) і\(u_2\), ми\(v_3\) замінюємо частиною, яка ортогональна до\(W_2=\text{Span}\{u_1,\:u_2\}=\text{Span}\{v_1,\:v_2\}\):
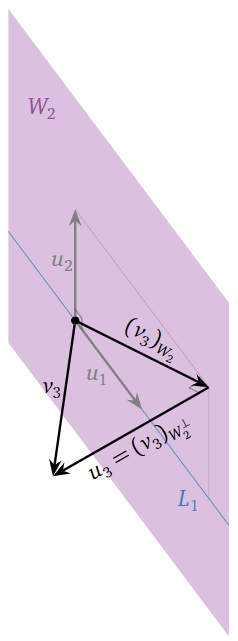
Малюнок\(\PageIndex{10}\)
Знайти ортогональну основу\(\{u_1,\:u_2,\:u_3\}\) для\(W=\text{Span}\{v_1,\:v_2,\:v_3\}\), де
\[v_1=\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)\quad v_2=\left(\begin{array}{c}-1\\4\\4\\-1\end{array}\right)\quad v_3=\left(\begin{array}{c}4\\-2\\-2\\0\end{array}\right).\nonumber\]
Рішення
Запускаємо Грам—Шмідта:
- \(u_1=v_1=\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)\)
- \(u_2=v_2-\frac{v_2\cdot u_1}{u_1\cdot u_1}u_1=\left(\begin{array}{c}-1\\4\\4\\-1\end{array}\right)-\frac{6}{4}\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)=\left(\begin{array}{c}-5/2\\5/2\\5/2\\-5/2\end{array}\right)\)
- \(\begin{aligned}u_3&=v_3-\frac{v_3\cdot u_1}{u_1\cdot u_1}u_1-\frac{v_3\cdot u_2}{u_2\cdot u_2}u_2 \\ &=\left(\begin{array}{c}4\\-2\\-2\\0\end{array}\right)-\frac{0}{24}\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)-\frac{-20}{25}\left(\begin{array}{c}-5/2\\5/2\\5/2\\-5/2\end{array}\right)=\left(\begin{array}{c}2\\0\\0\\-2\end{array}\right).\end{aligned}\)
Потім\(\{u_1,\:u_2,\:u_3\}\) робиться ортогональна основа для\(W\).
Ми побачили в доказі процесу\(1\) Грам—Шмідта\(m\), що для кожного\(i\) між і набір\(\{u_1,\:u_2,\cdots ,u_i\}\) є ортогональною основою для\(\text{Span}\{v_1,\:v_2,\cdots ,v_i\}\).
Якби ми почали з набору,\(\{v_1,\:v_2,\cdots ,v_m\}\) який лінійно залежний, то для деяких\(i\), вектор\(v_i\) знаходиться в\(\text{Span}\{v_1,\:v_2,\cdots ,v_{i−1}\}\) критерієм збільшення діапазону, Теорема 2.5.2 в розділі 2.5. Звідси
\[0=(v_i)_{\text{Span}\{v_1,\:v_2,\cdots ,v_{i-1}\}^{\perp}}=(v_i)_{\text{Span}\{u_1,\:u_2,\cdots u_{i-1}\}^{\perp}}=u_i.\nonumber\]
Ви можете використовувати процес Грам—Шмідта, щоб створити ортогональну основу з будь-якого набору, що охоплює: якщо деякі\(u_i=0\), просто викиньте\(u_i\) і\(v_i\), і продовжуйте.
