Skip to main content
LibreTexts - Ukrayinska

6: Ортогональність

  1. Last updated
  2. Save as PDF
  • Page ID
    62907

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Згадаймо в останній раз структуру цієї книги:

    1. Розв'яжіть матричне рівняння\(Ax=b\).
    2. Розв'яжіть матричне рівняння\(\lambda\),\(Ax=\lambda x\text{,}\) де є числом.
    3. Приблизно вирішуємо матричне рівняння\(Ax=b\).

    Тепер ми підійшли до третьої частини.

    Примітка\(\PageIndex{1}\)

    Приблизно вирішуємо матричне рівняння\(Ax=b.\)

    Пошук наближених розв'язків рівнянь зазвичай вимагає обчислення найближчого вектора на підпросторі до заданого вектора. Це стає проблемою ортогональності: потрібно знати, які вектори перпендикулярні підпростору.

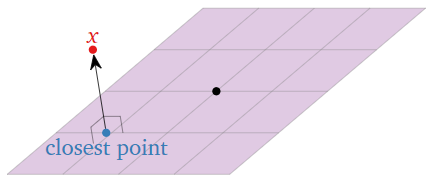
    clipboard_e4c312e06d8c1c7b40ae1ce8dfa3f77e5.png

    Малюнок\(\PageIndex{1}\)

    Спочатку ми визначимо ортогональність і навчимося знаходити ортогональні доповнення підпросторів у Розділі 6.1 та Розділі 6.2. Ядром цієї глави є Розділ 6.3, в якому ми обговорюємо ортогональну проекцію вектора на підпростір; це метод обчислення найближчого вектора на підпросторі до заданого вектора. Ці розрахунки стають простішими при наявності ортогонального набору, як ми побачимо в розділі 6.4. У розділі 6.5 ми представимо метод найменших квадратів орієнтовного розв'язування систем рівнянь, а також наведемо додатки до моделювання даних.

    Приклад\(\PageIndex{1}\)

    У моделюванні даних часто запитують: «на якій лінії повинні лежати мої дані?» Це можна вирішити за допомогою простого застосування методу найменших квадратів.

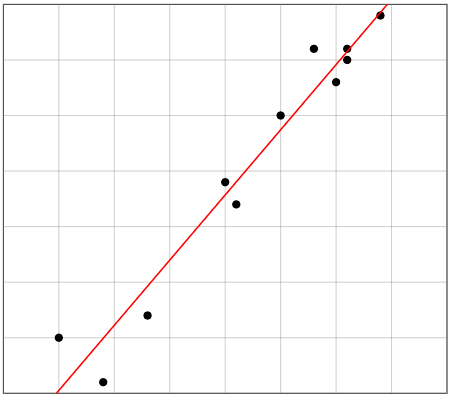
    clipboard_e9c04a2611d7045928bccedd7ad9c0a17.png

    Малюнок\(\PageIndex{2}\)

    Приклад\(\PageIndex{2}\)

    Гаусс винайшов метод найменших квадратів, щоб знайти найкраще пристосований еліпс: він правильно передбачив (еліптичну) орбіту астероїда Церера, коли він проходив позаду сонця в 1801 році.

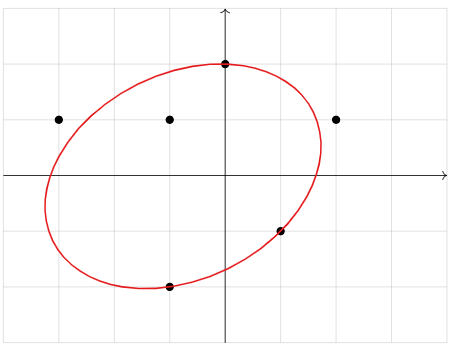
    clipboard_e8ec747dcd6cf56fd41cfcac28daede0f.png

    Малюнок\(\PageIndex{3}\)

     

    • 6.1: Точкові продукти та ортогональність
      У цьому розділі потрібно буде знайти найближчу точку на підпросторі до заданої точки. Найближча точка має властивість, що різниця між двома точками ортогональна, або перпендикулярна, до підпростору. З цієї причини нам потрібно розробити поняття ортогональності, довжини та відстані.
    • 6.2: Ортогональні доповнення
      Важливо буде обчислити множину всіх векторів, які є ортогональними до заданого набору векторів. Виявляється, що вектор ортогональний набору векторів тоді і тільки тоді, коли він ортогональний до прольоту цих векторів, який є підпростором, тому ми обмежуємося випадком підпросторів.
    • 6.3: Ортогональна проекція
      Нехай W є підпростором Rn і нехай x - вектор в Rn. У цьому розділі ми навчимося обчислювати найближчий вектор xW до x у W. Вектор xW називається ортогональною проекцією x на W. Це саме те, що ми будемо використовувати для майже вирішення матричних рівнянь.
    • 6.4: Ортогональні набори
    • 6.5: Метод найменших квадратів