15.5: Теорія кодування, групові коди

Last updated
Save as PDF

Page ID: 65071

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Проблема передачі

У цьому розділі ми познайомимо з основними ідеями теорії кодування і розглянемо розв'язки задачі кодування за допомогою групових кодів.

Уявіть собі ситуацію, в якій інформація передається між двома точками. Інформація набуває вигляду високих і низьких імпульсів (наприклад, радіохвиль або електричних струмів), які ми будемо позначати 1 і 0 відповідно. У міру надсилання та прийому цих імпульсів вони групуються в блоки фіксованої довжини. Довжина визначає, скільки інформації може міститися в одному блоці. Якщо довжина є,$r\text{,}$ існують$2^r$ різні значення, які може мати блок. Якщо інформація, що надсилається, має форму тексту, кожен блок може бути символом. У такому випадку довжина блоку може становити сім, так що значення$2^7 = 128$ блоку можуть представляти літери (як великі, так і малі регістр), цифри, розділові знаки і так далі. Під час передачі даних шум може змінювати сигнал так, що отримане відрізняється від того, що надсилається. Малюнок$\PageIndex{1}$ ілюструє проблему, з якою можна зіткнутися, якщо інформація передається між двома точками.

$clipboard_e18c4e20ab50f2d417976e617d1260b67.png$ Малюнок$\PageIndex{1}$: Галаслива передача

Шум - це факт життя кожного, хто намагається передавати інформацію. На щастя, у більшості ситуацій ми могли очікувати, що високий відсоток імпульсів, які надсилаються, буде прийнятий належним чином. Однак при передачі великої кількості імпульсів зазвичай виникають деякі помилки через шум. На решту обговорення ми зробимо припущення про характер шуму і повідомлення, яке ми хочемо відправити. Відтепер ми будемо називати імпульси бітами.

Будемо вважати, що наша інформація надсилається по двійковому симетричному каналу. Під цим ми маємо на увазі, що будь-який єдиний біт, який передається, буде прийнятий неправильно з певною фіксованою ймовірністю,$p\text{,}$ незалежно від значення біта. Величина,$p$ як правило, досить мала. Для ілюстрації процесу ми припустимо те,$p = 0.001\text{,}$ що в реальному світі вважалося б дещо великим. Оскільки$1 - p = 0.999\text{,}$ ми можемо очікувати$99.9\%$, що всі біти будуть правильно отримані.

Припустимо, що наше повідомлення складається з 3000 біт інформації, яка буде відправлена блоками по три біти кожен. При оцінці способу передачі будуть враховані два фактори. Перша - ймовірність того, що повідомлення отримано без помилок. Другий - це кількість бітів, які будуть передані для того, щоб відправити повідомлення. Ця величина називається швидкістю передачі:

\ begin {рівняння*}\ textrm {Швидкість} =\ frac {\ textrm {Довжина повідомлення}} {\ textrm {Кількість переданих бітів}}\ end {рівняння*}

Як і слід було очікувати, коли ми розробляємо методи підвищення ймовірності успіху, швидкість зменшиться.

Припустимо, що ми ігноруємо шум і передаємо повідомлення без будь-якого кодування. Імовірність успіху$0.999^{3000}= 0.0497124\text{.}$ Тому ми успішно отримуємо повідомлення лише у абсолютно правильній$5\%$ формі менше часу. Швидкість,$\frac{3000}{3000} = 1$ звичайно, не компенсує цю погану ймовірність.

Нашою стратегією підвищення шансів на успіх буде надсилання закодованого повідомлення через двійковий симетричний канал. Кодування буде виконано таким чином, щоб можна було виявити і виправити невеликі помилки. Ця ідея проілюстрована на рис$\PageIndex{2}$.

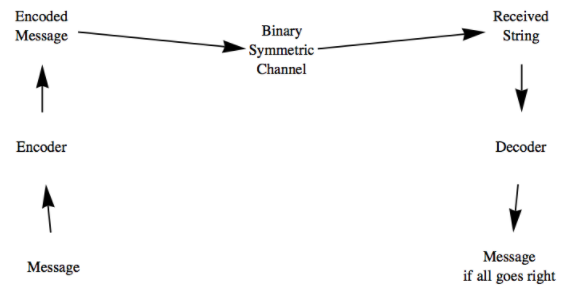$clipboard_e1db747a127cf5933e608483ca9935140.png$ Малюнок$\PageIndex{2}$: Процес кодування

У наших прикладах функції, які будуть відповідати нашим пристроям кодування і декодування, будуть все це гомоморфізми між декартовими добутками$\mathbb{Z}_2\text{.}$

Виявлення помилок

Припустимо, що кожен блок з трьох бітів$a = \left(a_1, a_2 , a_3 \right)$ закодований функцією$e: \mathbb{Z}_2{}^3\to \mathbb{Z}_2{}^4\text{,}$ де

\ begin {рівняння*} e (a) =\ лівий (a _1, a _2, a _3, a_1+_2a_2+_2a_3\ правий)\ кінець {рівняння*}

При отриманні закодованого блоку чотири біта, ймовірно, все будуть правильними (вони коректні приблизно$99.6\%$ в той час), але доданий біт, який надсилається, дасть можливість виявити поодинокі помилки в блоці. Зверніть увагу,$e(a)$ що при передачі сума його складових становить$a_1+_2 a_2 +_2 a_3+_2 \left( a_1+_2 a_2+_2 a_3\right)= 0\text{,}$ так як$a_i+a_i=0$ в$\mathbb{Z}_2\text{.}$

Якщо будь-який одиночний біт спотворюється шумом, сума отриманих бітів буде дорівнює 1. Останній біт$e(a)$ називається бітом парності. Помилка парності виникає, якщо сума отриманих бітів дорівнює 1. Оскільки більше однієї помилки малоймовірно, коли$p$ вона невелика, можна виявити високий відсоток всіх помилок.

На приймальному кінці функція декодування діє на чотирибітний блок$b = \left(b_1,b _2 ,b_3,b_4 \right)$ з функцією$d: \mathbb{Z}_2{}^4\to \mathbb{Z}_2^4\text{,}$ де

\ begin {рівняння*} d (b) =\ лівий (b_1, b _2, b_3, b_1+_2b _2b _2 +_2b_3+_2b_4\ правий)\ кінець {рівняння*}

Четвертий біт називається бітом перевірки парності. Якщо помилки парності не виникає, перші три біти записуються як частина повідомлення. Якщо виникає помилка парності, ми будемо вважати, що повторна передача цього блоку може бути запитана. Цей запит може мати форму автоматичного$d(b)$ надсилання біта перевірки парності назад до джерела. Якщо отримано 1, попередній блок передається повторно; якщо отримано 0, то відправляється наступний блок. Це припущення двостороннього зв'язку є значним, але бажано зробити цю систему кодування корисною. Розумно очікувати, що ймовірність помилки передачі в зворотному напрямку також дорівнює 0,001. Не вдаючись в подробиці, повідомимо, що ймовірність успіху становить приблизно 0,990, а ставка приблизно 3/5. Швидкість включає передачу біта перевірки паритетності до джерела.

Виправлення помилок

Далі ми розглянемо процес кодування, який може виправити помилки на приймальному кінці так, що потрібна тільки одностороння комунікація. Перш ніж ми почнемо, нагадайте, що кожен елемент$\mathbb{Z}_2{}^n\text{,}$$n \geq 1\text{,}$ є своїм оберненим; тобто,$-b = b\text{.}$ Отже,$a - b = a + b\text{.}$

Галасливі трибітові блоки повідомлень важко передавати, оскільки вони настільки схожі один на одного. Якщо$a$ і$b$ знаходяться в$\mathbb{Z}_2{}^3\text{,}$ їх відмінності,$a +_2 b\text{,}$ можна розглядати як міру того, наскільки вони близькі. Якщо$a$ і$b$ відрізняються лише однією бітовою позицією, одна помилка може змінити одну в іншу. Кодування, яке ми введемо, приймає блок$a = \left(a_1, a_2, a_3 \right)$ і створює блок довжиною 6, який називається кодовим словом Кодові слова вибираються так, щоб вони знаходилися далі один від одного, ніж повідомлення.$a\text{.}$ Насправді кожне кодове слово буде відрізнятися один від одного кодове слово мінімум на три біти. Як результат, будь-яка одна помилка не підштовхне кодове слово досить близько до іншого кодового слова, щоб викликати плутанину. Тепер про деталі.

Нехай$G=\left( \begin{array}{cccccc} 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ \end{array} \right)\text{.}$ Ми$G$ називаємо матрицю генератора для коду, і нехай$a = \left(a_1, a_2, a_3 \right)$ буде наше повідомлення.

Визначити$e : \mathbb{Z}_2{}^3 \to \mathbb{Z}_2{}^6$ по

\ begin {рівняння*} e (a) = a G =\ ліворуч (a_1, a_2, a_3, a_4, a_5, a_6\ праворуч)\ end {рівняння*}

де

\ begin {рівняння*}\ почати {масив} {r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} a_4 &= & a_1 & {} +_2 {} & a_2 {} & a_2 &\ a_5 &= & a_1 & & {} +_2 {} & a_3\ a_6 &= & a_1 & & {} +_2\ a_6 2 & {} +_2 {} & a_3\\\ end {масив}\ end {рівняння*}

Зверніть увагу, що$e$ це гомоморфізм. Крім того, якщо$a$ і$b$ є окремими елементами,$\mathbb{Z}_2{}^3\text{,}$ то$c = a + b$ має принаймні одну координату, рівну 1. Тепер розглянемо різницю між$e(a)$ і$e(b)\text{:}$

\ begin {рівняння*}\ почати {спліт} e (a) + e (b) &= e (a + b)\\ & = e (c)\\ & =\ лівий (d_1, d_2, d_3, d_4, d_5, d_6\ праворуч)\\ кінець {спліт}\ кінець {рівняння*}

Незалежно від того,$c$ має 1, 2 або 3 одиниці,$e(c)$ повинні мати принаймні три. У цьому можна переконатися, розглянувши три випадки окремо. Наприклад, якщо$c$ має один, два біти парності також 1. Тому$e(a)$ і$e(b)$ розрізняються як мінімум на три біти.

Тепер розглянемо проблему розшифровки кодових слів. Уявіть, що кодове слово,$e(a)\text{,}$ передається, і$b= \left(b_1, b_2, b_3,b_4, b_5, b_6\right)$ отримано. На приймальному кінці ми знаємо формулу для$e(a)\text{,}$ і якщо в передачі не відбулося жодної помилки,

\ begin {рівняння*}\ почати {масив} {c} b_1= a_1\\ b_2=a_2\\ b_3=a_3\ b_4=a_1+_2a_2\\ b_5=a_1+_2a_3\\ b_6 = a_2+_2a_3\\ кінець {масив} @ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} b_1 & +_2 & b_2 & &+_2& b_4& & &&=0\\ b_1 & & підсилювач; +_2 &b_3& & +_2&b_5 & &=0\\ & & b_2 & +_2 &b_3& & &&&+_2 &b_6&=0\\ кінець {масив}\ кінець {рівняння*}

Три рівняння праворуч називаються рівняннями перевірки парності. Якщо будь-який з них не відповідає дійсності, сталася помилка. Цю перевірку помилок можна описати у вигляді матриці.

Нехай

\ begin {рівняння*} P=\ ліворуч (\ begin {масив} {ccc} 1 & 1\\ 1 & 0 & 1\\ 0 & 1\\ 1\ 1 & 0 & 0\\ 0 & 1\ 0 & 0\\ 0 & 1\\\ end {масив}\ праворуч)\ кінець {рівняння*}

$P$називається матрицею перевірки парності для цього коду. Тепер$p(b) = b P\text{.}$ визначаємо$p:\mathbb{Z}_2{}^6 \to \mathbb{Z}_2{}^3$ по$p(b)$ Називаємо синдром отриманого блоку. Наприклад,$p(0,1,0,1,0,1)=(0,0,0)$ і$p(1,1,1,1,0,0)=(1,0,0)$

Зверніть увагу, що$p$ це також гомоморфізм. Якщо синдром блоку є,$(0, 0, 0)\text{,}$ ми можемо бути майже впевнені, що блок повідомлень$\left(b_1, b_2, b_3\right)\text{.}$

Далі переходимо до методу виправлення помилок. Незважаючи на те, що кодових слів всього вісім, по одному на кожне трибітове значення блоку, набір можливих отриманих блоків -$\mathbb{Z}_2{}^6\text{,}$ з 64 елементами. Припустимо, що$b$ це не кодове слово, але що воно відрізняється від кодового слова рівно на один біт. Іншими словами, це результат єдиної помилки при передачі. Припустимо, що$w$ це кодове слово,$b$ яке найближче до і що вони відрізняються в першому біті. Потім$b + w = (1, 0, 0, 0, 0, 0)$ і

\ begin {рівняння*}\ почати {спліт} p (b) & = p (b) + p (w)\ quad\ textrm {оскільки} p (w) = (0, 0, 0)\ &=p (b+w)\ quad\ textrm {оскільки} p\ textrm {є гомоморфізмом}\\ & =p (1,0,0,0,0,0)\ & = (1,1,0)\\ кінець {спліт}\ кінець {рівняння*}

Зауважте, що ми не вказали$b$ або$w\text{,}$ лише те, що вони відрізняються у першому біті. Тому, якщо$b$ отримано, ймовірно, була помилка в першому біті і$p(b) = (1, 1, 0)\text{,}$ передане кодове слово було ймовірно$b + (1, 0, 0, 0, 0, 0)$ і блок повідомлень був$\left(b_1+_2 1, b_2, b_3\right)\text{.}$ Той же аналіз можна зробити, якщо$b$ і$w$ відрізнятися в будь-якому з інших п'яти бітів.

Цей процес можна описати з точки зору витрат. $W$Дозволяти набір кодових слів; тобто,$W = e\left(\mathbb{Z}_2{}^3 \right)\text{.}$ Оскільки$e$ є гомоморфізмом,$W$ є підгрупою$\mathbb{Z}_2{}^6\text{.}$ Розглянемо факторну групу$\left.\mathbb{Z}_2{}^6\right/W\text{:}$

\ begin {рівняння*}\ lvert\ mathbb {Z} _2 {} ^6/W\ rvert =\ frac {\ lvert\ mathbb {Z} _2 {} ^6\ rvert} {\ lvert W\ rvert} =\ frac {64} {8} =8\ кінець {рівняння*}

Припустимо, що$b_1$ і$b_2$ є представниками одного і того ж косету. Тоді$b_1= b_2+w$ для деяких$w$ в$W\text{.}$ Отже,

\ begin {рівняння*}\ почати {спліт} p\ ліворуч (b _1\ праворуч) &= p\ ліворуч (b_1\ праворуч) + p (w)\ quad\ textrm {так} p (w) = (0, 0, 0)\\ &= p\ лівий (b_1 + w\ правий)\\ &= p\ лівий (b_2\ правий)\\ кінець {спліт}\ end {рівняння*}

і так$b_1$ і$b_2$ мають той же синдром.

Нарешті, припустимо, що$d_1$ і$d_2$ різні, і обидва мають лише одну координату, рівну 1. Тоді$d_1+d_2$ має рівно два. Зверніть увагу, що ідентичність$\mathbb{Z}_2{}^6\text{,}$$(0, 0, 0, 0, 0, 0)\text{,}$ повинна бути в$W\text{.}$ Since$d_1+d_2$ відрізняється від ідентичності на два біти,$d_1+d_2 \notin W\text{.}$ Отже$d_1$ і$d_2$ належать до різних косетів. Вищевикладене міркування служить доказом наступної теореми.

Теорема$\PageIndex{1}$

Існує система видатних представників$\left.\mathbb{Z}_2{}^6\right/W$ таких, що кожен з шестибітних блоків, що мають один 1, є відмінним представником власної косети.

Тепер ми можемо описати процес виправлення помилок. Спочатку зіставте кожен з блоків з єдиним 1 з його синдромом. Крім того, зіставте ідентичність$W$ з синдромом$(0, 0, 0)$, як у таблиці нижче. Так як існує вісім косетів,$W\text{,}$ виберіть будь-який представник восьмої косети, який слід виділити. Це косет з синдромом$(1, 1, 1)\text{.}$

\ begin {рівняння*}\ почати {масив} {c|c}\ begin {масив} {c}\ textrm {Синдром}\\ hline\ begin {масив} {ccc} 0 & 0\ 1 & 0\\ 1 & 0 & 1\\ 0 & 1\ 1\ 1 & 1\ 1\ 1 & 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\ 1\\ 1 & 1 & 1\\\ кінець {масив}\\ кінець {масив} &\ begin { масив} {c}\ текст {Помилка}\ текст {Виправлення}\\ hline\ begin {масив} {cccccc} 0 & 0 & 0 & 0\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0 & 0 & 1\\ кінець {масив}\\ кінець {масив}\\ кінець {масив}\ кінець {рівняння*}

Коли блок$b$ отриманий, потрібно лише обчислити синдром,$p(b)\text{,}$ і додати до$b$ виправлення помилок, що відповідає$p(b)\text{.}$

Ми завершимо цей приклад, обчисливши ймовірність успіху для нашої гіпотетичної ситуації. Це$\left(0.999^6 + 6 \cdot 0.999^5 \cdot 0.001\right)^{1000}=0.985151\text{.}$ Ставка для цього коду$\frac{1}{2}\text{.}$

Приклад$\PageIndex{1}$: Another Linear Code

Розглянемо лінійний код з матрицею генератора

\ begin {рівняння*} G =\ лівий (\ begin {масив} {ccccc} 1 & 1 & 0 & 0\\ 0 & 1 & 1 & 1 & 0 & 0\ 0 & 0 & 0 & 0 & 0 & 0 & 1\\\ end {масив}\ праворуч). \ end {рівняння*}

Так як$G$ саме$3 \times 5\text{,}$ цей код кодує три біти в п'ять біт. Природне питання, яке потрібно задати, полягає в тому, що виявлення чи виправлення це дозволяє? Відповісти на це питання ми можемо, побудувавши матрицю перевірки парності. Ми спостерігаємо, що якщо$\vec{b}=(b_1, b_2, b_3)$ функція кодування

\ begin {рівняння*} e (\ vec {b}) =\ vec {b} G = (b_1, b_1+b_2, b_2, b_1+b_3, b_3)\ end {рівняння*}

де доповнення мод 2 доповнення. Якщо ми отримаємо п'ять бітів$(c_1,c_2,c_3,c_4,c_5)$ і жодної помилки не сталося, наступні два рівняння будуть вірними.

\[\begin{align}c_1+c_2+c_3&=0\label{eq:1} \\ c_1+c_4+c_5&=0\label{eq:2}\end{align}\]

Зверніть увагу, що в цілому кількість рівнянь перевірки парності дорівнює кількості зайвих бітів, які додаються функцією кодування. Ці рівняння еквівалентні одноматричному рівнянню$(c_1,c_2,c_3,c_4,c_5)H = \vec{0}\text{,}$, де

\ begin {рівняння*} H =\ left (\ begin {масив} {cc} 1 & 1\\ 1 & 0\\ 1 & 0\\ 0 & 1\\ 0 & 1\\ 0 & 1\\\ end {масив}\ праворуч)\ кінець {рівняння*}

З першого погляду ми бачимо, що цей код не виправляє більшість однобітових помилок. Припустимо$\vec{e}=(e_1,e_2,e_3,e_4,e_5)$, додана помилка при передачі п'яти біт. Зокрема, припустимо, що 1 додається (мод 2) в позиції,$j\text{,}$ де$1 \leq j\leq 5$ і інші$\vec{e}$ координати 0. Тоді, коли ми обчислюємо синдром нашої отриманої передачі, ми бачимо, що

\ почати {рівняння*}\ vec {c} H = (\ vec {b} G +\ vec {e}) H = (\ vec {b} G) H +\ vec {e} H =\ vec {e} H\ end {рівняння*}

Але$\vec{e}H$ це$j^{th}$ рядок$H\text{.}$ Якщо синдром є$(1,1)$ ми знаємо, що помилка сталася в позиції 1, і ми можемо виправити її. Однак, якщо помилка знаходиться в будь-якому іншому положенні, ми не можемо визначити її місце розташування. Якщо синдром є,$(1,0)\text{,}$ то помилка могла статися або в положенні 2, або в положенні 3. Цей код виявляє всі однобітові помилки, але виправляє лише одну п'яту з них.

вправи

Вправа$\PageIndex{1}$

Якщо використовується код виявлення помилок, як би ви діяли на наступних отриманих блоках?

$\displaystyle (1, 0, 1, 1)$
$\displaystyle (1, 1, 1, 1)$
$\displaystyle (0, 0, 0, 0)$

Відповідь

Виявлена помилка, оскільки було отримано непарне число 1; попросити повторну передачу.
Помилка не виявлена; прийміть цей блок.
Помилка не виявлена; прийміть цей блок.

Вправа$\PageIndex{2}$

Висловіть функції кодування та декодування коду виявлення помилок за допомогою матриць.

Вправа$\PageIndex{3}$

Якщо використовується код, що виправляє помилки з цього розділу, як би ви декодували наступні блоки? Очікуйте помилку, яку неможливо виправити за допомогою одного з них.

$\displaystyle (1,0,0,0,1,1)$
$\displaystyle (1,0,1,0,1,1)$
$\displaystyle (0,1,1,1,1,0)$
$\displaystyle (0,0,0,1,1,0)$
$\displaystyle (1,0,0,0,0,1)$
$\displaystyle (1,0,0,1,0,0)$

Відповідь

Синдром =$(1,0,1)\text{.}$ Виправлено кодоване повідомлення,$(1,1,0,0,1,1)$ і оригінальне повідомлення було$(1, 1, 0)\text{.}$
Синдром =$(1,1,0)\text{.}$ Виправлено кодоване повідомлення,$(0,0,1,0,1,1)$ і оригінальне повідомлення було$(0, 0, 1)\text{.}$
Синдром =$(0,0,0)\text{.}$ Немає помилок, закодоване повідомлення$(0,1,1,1,1,0)$ і вихідне повідомлення було$(0, 1, 1)\text{.}$
Синдром =$(1, 1,0)\text{.}$ Виправлено кодоване повідомлення,$(1,0,0,1,1,0)$ і оригінальне повідомлення було$(1, 0, 0)\text{.}$
Синдром =$(1,1,1)\text{.}$ Цей синдром виникає тільки в тому випадку, якщо два біти були переключені. Ніяка надійна корекція неможлива.
Синдром =$(0,1,0)\text{.}$ Виправлено кодоване повідомлення,$(1,0,0,1,1,0)$ і оригінальне повідомлення було$(1, 0, 0)\text{.}$

Вправа$\PageIndex{5}$

Розглянемо лінійний код, який визначається матрицею генератора

\ begin {рівняння*} G=\ left (\ begin {масив} {cccc} 1 & 0 & 0\ 0 & 1 & 1 & 1\\\ end {масив}\ праворуч)\ кінець {рівняння*}

Який розмір блоків кодує цей код і яка довжина кодових слів?
Які кодові слова для цього коду?
За допомогою цього коду ви можете виявити однобітові помилки? Чи можете ви виправити всі, деякі, або ніяких однобітових помилок?

Відповідь: $G$Дозволяти$9 \times 10$ матриця, отримана шляхом доповнення$9\times 9$. Функція,$e:\mathbb{Z}_2{}^9\to \mathbb{Z}_2{}^{10}$ визначена за,$e(a) = a G$ дозволить нам виявити поодинокі помилки, оскільки завжди$e(a)$ буде мати парну кількість.

Вправа$\PageIndex{6}$: Rectangular Codes

Щоб побудувати прямокутний код, ви розділите ваше повідомлення на блоки довжини$m$, а потім коефіцієнт$m$ на$k_1\cdot k_2$ і організувати біти в$k_1 \times k_2$ прямокутному масиві, як на малюнку нижче. Потім ви додаєте біти парності уздовж правої та нижньої частини рядків та стовпців. Кодове слово потім читається рядок за рядком.

\ begin {рівняння*}\ begin {масив} {cccccc}\ чорний квадрат &\ чорний квадрат &\ чорний квадрат &\ cdots &\ чорний квадрат\\ чорний квадрат &\ чорний квадрат &\ cdots &\ чорний квадрат &\\ квадрат\\ vdots &\ vdots\\ чорний квадрат &\ чорний квадрат &\ чорний квадрат &\ cdots &\ чорний квадрат &\ квадрат\\ квадрат &\ квадрат &\ квадрат &\ cdots &\ квадрат &\\ кінець {масив}\ quad\ begin {масив} {c}\ textrm {}\ blacksquare =\ textrm {повідомлення}\ textrm {текст} trm {біт}\\\ кінець { масив}\ end {рівняння*}

Наприклад, якщо$m$ дорівнює 4, то наш єдиний вибір - масив 2 на 2. Повідомлення 1101 буде закодовано як

\ begin {рівняння*}\ почати {масив} {cc|c} 1 & 1 & 0\\ 0 & 1\\ hline 1\\ hline 1 & 0 & 0 & 0 &\\\ end {масив}\ кінець {рівняння*}

і кодове слово - рядок 11001110.

Припустимо, що вам було надіслано чотири бітові повідомлення за допомогою цього коду і ви отримали наступні рядки. Якими були повідомлення, припускаючи не більше однієї помилки при передачі закодованих даних?
1. 11011000
2. 01110010
3. 1000111
Якщо ви закодовані$n^2$ біти таким чином, якою буде швидкість коду?
Прямокутні коди - лінійні коди. Для прямокутного коду 3 на 2, які матриці генератора і перевірки парності?

Вправа$\PageIndex{7}$

Припустимо, що код у$\PageIndex{1}$ прикладі розширено, щоб додати стовпець

\ begin {рівняння*}\ left (\ begin {масив} {c} 0\\ 1\\ 1\\ end {масив}\ праворуч)\ end {рівняння*}

до матриці генератора$G\text{,}$ можна виправити всі однобітові помилки? Поясніть свою відповідь.

Відповідь

Так, ви можете виправити всі однобітові помилки, оскільки матриця перевірки парності для розширеного коду

\ begin {рівняння*}
H =\ ліворуч (\ begin {масив} {ccc}
1 & 1\\
1 & 0\\ 1\
1\ 1 & 0 & 1\\
0 & 1\ 0 & 1\\
0 & 1\\ 0 & 1\
0 & 1\\ 0 & 1\\
\ end {масив}\ право).
\ end {рівняння*}

Оскільки кожен можливий синдром однобітових помилок унікальний, ми можемо виправити будь-яку помилку.