Skip to main content
LibreTexts - Ukrayinska

1.2: Приклади

  1. Last updated
  2. Save as PDF
  • Page ID
    64399

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Припустимо, у нас є шахова дошка, і колекція плиток, як доміно, кожна з яких має розмір двох квадратів на шаховій дошці. Чи можна шахову дошку покривати доміно? Спочатку нам потрібно чітко визначитися з правилами: дошка покрита, якщо доміно покладені так, щоб кожен покривав рівно два квадрати дошки; жодне доміно не перекривається; і кожен квадрат покритий. Відповідь проста: просто виклавши 32 доміно рядами, дошку можна накрити. Щоб завдання було цікавіше, дозволяємо дошці бути прямокутної будь-якого розміру, і дозволяємо прибрати з дошки деякі квадрати. Що можна сказати про те, чи можна покрити залишилася дошку? Це така дошка, наприклад:

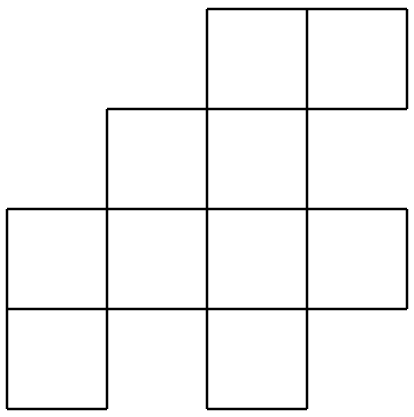
    clipboard_ef7c12dcf93b2cea03e5d63b01b85d23a.png
    Малюнок\(\PageIndex{1}\)

    Що ми можемо сказати? Тут просте спостереження: кожне доміно має охоплювати два квадрати, тому загальна кількість квадратів повинна бути парною; дошка вище має парну кількість квадратів. Цього достатньо? Не дуже важко переконати себе, що цю дошку не можна охопити; чи є якийсь загальний принцип роботи? Припустимо, ми перемальовуємо дошку, щоб підкреслити, що вона дійсно є частиною шахової дошки:

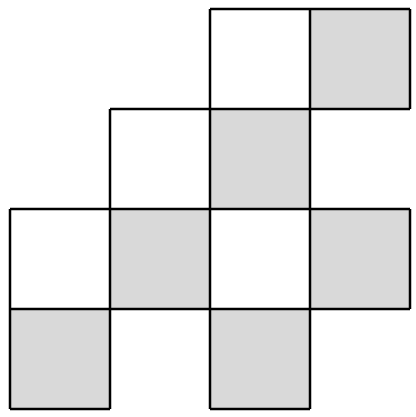
    clipboard_e7307c7fea737286b2097229983a0a0d2.png
    Малюнок\(\PageIndex{2}\)

    Ага! Кожна плитка повинна покривати один білий і один сірий квадрат, але є чотири перших і шість останніх, так що це неможливо. Тепер у нас є вся картина? Ні; наприклад:

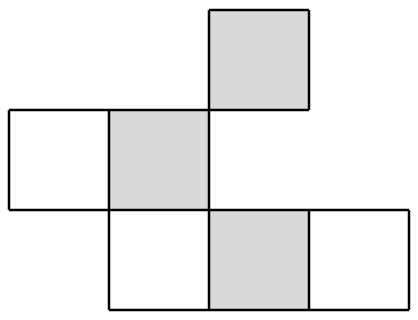
    clipboard_eb8e562dd723c035fb23c7d937e2b09dc.png
    Малюнок\(\PageIndex{3}\)

    Сірий квадрат у верхньому правому куті явно не може бути покритий. На жаль, нелегко констатувати умову, яка повністю характеризує дошки, які можна покрити; ми побачимо цю проблему знову. Відзначимо, однак, що цю задачу також можна представити у вигляді графічної задачі. Ми вводимо вершину, відповідну кожному квадрату, і з'єднуємо дві вершини ребром, якщо пов'язані з ними квадрати можуть бути покриті одним доміно; ось попередня дошка:

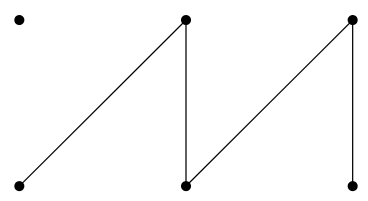
    clipboard_e8c7052a9b183f72eb2ef850745322c6d.png
    Малюнок\(\PageIndex{4}\)

    Тут верхній ряд вершин представляє сірі квадрати, нижній ряд - білі квадрати. Доміно тепер відповідає ребру; покриття доміно відповідає колекції ребер, які не мають кінцевих точок і які трапляються (тобто торкаються) усіх шести вершин. Оскільки жодне ребро не впадає з верхньою лівою вершиною, кришки немає.

    Можливо, найвідоміша проблема в теорії графів стосується забарвлення карти: Враховуючи карту деяких країн, скільки кольорів потрібно для фарбування карти, щоб країни, які мають кордон, отримували різні кольори? Довго припускали, що будь-яка карта може бути пофарбована чотирма кольорами, і це остаточно було доведено в 1976 році. Ось приклад невеликої карти, пофарбованої чотирма кольорами:

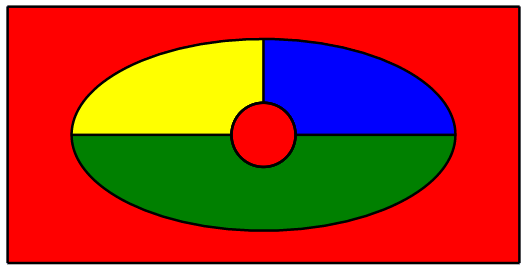
    clipboard_ece422175eeb04754028beff35e9de921.png
    Малюнок\(\PageIndex{5}\)

    Typically this problem is turned into a graph theory problem. Suppose we add to each country a capital, and connect capitals across common boundaries. Coloring the capitals so that no two connected capitals share a color is clearly the same problem. For the previous map:

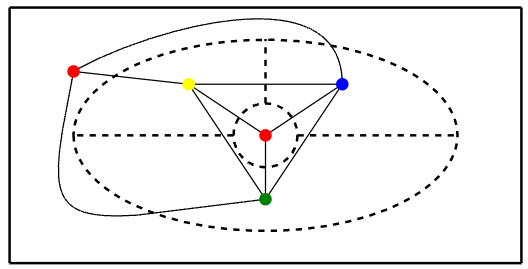
    clipboard_e417192b8601a0f8dffbedbc8d79a030a.png
    Figure \(\PageIndex{6}\)

    Any graph produced in this way will have an important property: it can be drawn so that no edges cross each other; this is a planar graph. Non-planar graphs can require more than four colors, for example this graph:

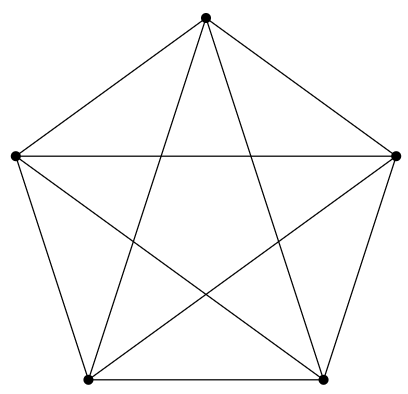
    clipboard_e7355daa25b6157c936b7ed97fd6239d5.png
    Figure \(\PageIndex{7}\)

    This is called the complete graph on five vertices, denoted \(K_5\); in a complete graph, each vertex is connected to each of the others. Here only the "fat'' dots represent vertices; intersections of edges at other points are not vertices. A few minutes spent trying should convince you that this graph cannot be drawn so that its edges don't cross, though the number of edge crossings can be reduced.

    Contributors and Attributions