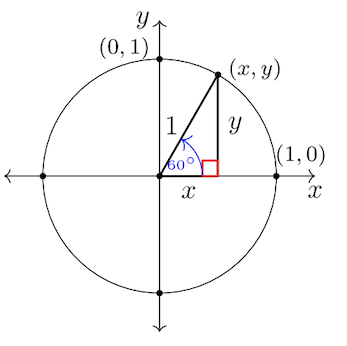
7.1: Одиничне коло

Last updated

Oct 27, 2022
Save as PDF
- 7: Тригонометрія
- 7.2: Довідкові кути

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

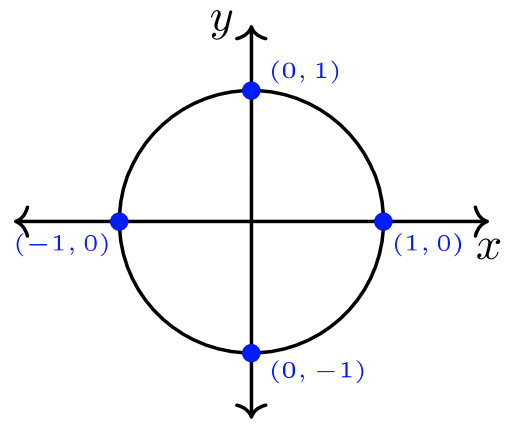
Основні поняття тригонометрії розвиваються з кола з радіусом, рівним $1$ одиниці, намальованої в $xy$ -координатної площині, по центру на початку. Цьому колу дано назву: одиничний коло (Малюнок $7.1.1$ нижче). Подібно до $12$ годинного годинника зі значеннями часу від $1$ до $12$ , тригонометричні функції є періодичними, тобто однакові значення відтворюються з кожним $360˚$ оборотом.

Рисунок Template:index: Кути в стандартному положенні

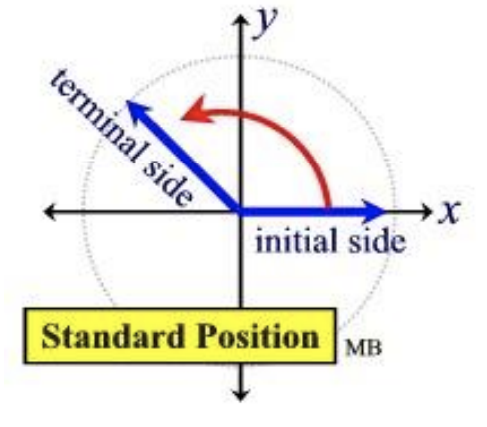
Кут знаходиться в стандартному положенні (див. Рис. $7.1.2$ Вище), якщо його початкова сторона знаходиться вздовж позитивної $x$ осі, а його вершина - у точці початку: $(0,0)$ . Наступні кути знаходяться в стандартному положенні. Кут, який обертається в напрямку проти годинникової стрілки, є позитивним. Кут, який обертається за годинниковою стрілкою, є негативним.

Рисунок Template:index: Позитивний кут у стандартному положенні.

Рисунок Template:index:: Від'ємний кут у стандартному положенні.

Котермінальні кути

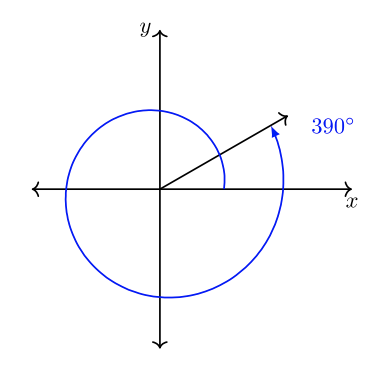
Кажуть, що два або більше стандартних кутів, які поділяють спільні сторони терміналу, є котермінальними кутами. Наприклад, $30˚$ і $390˚$ є котермінальними кутами.

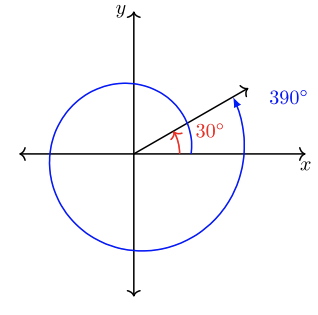
$clipboard_edae1eab80f059ab6160333bcf21dad75.png$

Більш формально: Кожен кут $B$ співтермінальний з кутом $A$ де $B = A + 360˚k$ , $k =$ будь-яке ціле число.

Приклад Template:index

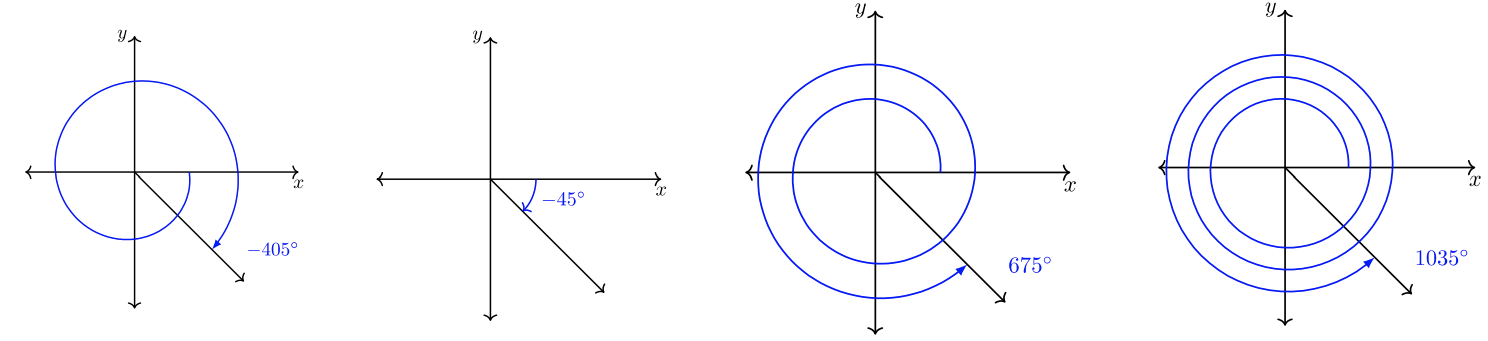
Вираз $315˚ + 360˚k$ дає кути співтермінал с $315˚$ . Створіть котермінальні кути, які формує рівняння, використовуючи наступні $k$ -значення: $k = −2, −1, 1, 2$ . Потім накидайте кути.

Рішення

Підставляємо задані $k$ -значення в вираз $315˚ + 360˚k$ .

$k = -2$	$k = -1$	$k = 1$	$k = 2$
$315˚ + 360˚(\textcolor{red}{-2}) = -405˚$	$315˚ + 360˚(\textcolor{red}{-1}) = -45˚$	$315˚ + 360˚(\textcolor{red}{1}) = -675˚$	$315˚ + 360˚(\textcolor{red}{2}) = 1035˚$

Знизу накидаються кути. Ви бачите, що кожен кут має одну і ту ж клемну сторону? Всі чотири кути є співтермінальними з $315˚$ і співтермінальними один з одним.

$clipboard_e817c28fbb916447571993b1ba5b92c18.png$

Коло по центру на початку

Кожна $(x, y)$ впорядкована пара на колі пов'язана з прямокутним трикутником. Прямокутний трикутник має горизонтальну відстань $x$ $y$ , відстань по вертикалі та гіпотенузу = радіус = $r$ .

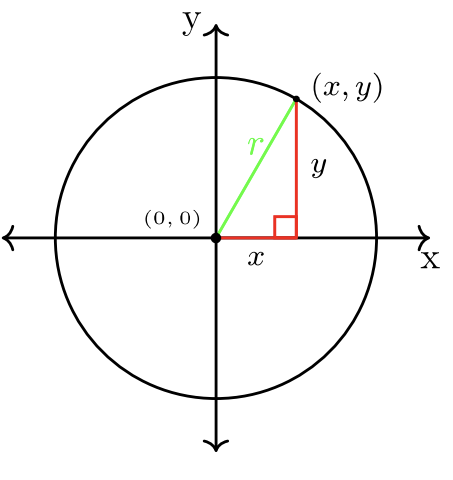
$clipboard_ea4f396a40a55f4929eb6dd6b1ad1cbda.png$

Рівняння кола

Рівняння окружності радіуса з $r$ центром у початку:

$x^2 + y^2 = r^2$

Примітка: $x$ -coordinate і $y$ -coordinate можуть приймати негативні значення, залежно від квадранта кінцевої сторони кута.

Приклад Template:index

Знайти $y$ -координату точки A, $\left(−\dfrac{5}{9} , y \right)$ якщо точка A лежить в QIII на одиничному колі.

Рішення

Одинична окружність має радіус $r = 1$ . Тригонометрія з'єднує алгебру і геометрію з наочними ескізами. Створіть ескіз, перш ніж стрибати в розчин. Це допоможе вам побачити відповідь.

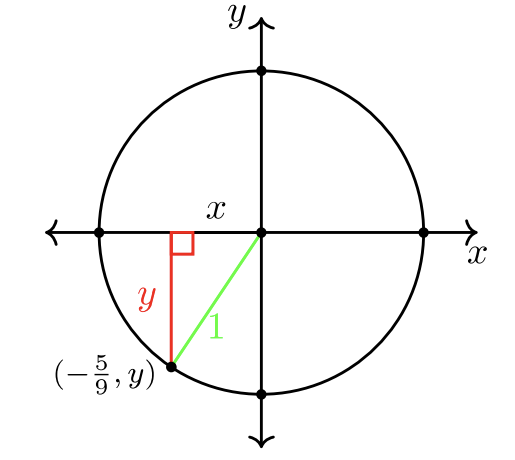
$clipboard_ed6aa5e0ff457f2cdadcf335269d53625.png$

$\begin{array} &\left(−\dfrac{5}{9}\right)^2 + y^2 &= 1^2 &\text{Substitute $x = −\dfrac{5}{9}$ і $r = 1$ в рівняння кола.}\\ dfrac {25} {81} + y^2 &= 1 &\ text {Спрощення.}\\ y^2 &= 1 -\ dfrac {25} {81} &\ text {{81} {81} {81} {{81} {{81} {{81} {dfrac {25} {81} {81} {81} {81} текст {Знайти РК-дисплей.}\\ y^2 &=\ dfrac {56} {81} &\ text {Спрощення.} $\dfrac{25}{81}$ \\ sqrt {y^2} &= ±\ sqrt {\ dfrac {56} {81}} &\ text {Квадратний корінь з обох сторін.}\\ y &= -\ dfrac {\ sqrt {56}} {9} &\ text {Виберіть правильне значення знака. $y < 0$ у III кварталі.}\\ y &= −\ dfrac {2\ sqrt {14}} {9} &\ text {Спрощення радикала.} \ end {масив}$

Спеціальні прямокутні трикутники

Використовуючи теорему Піфагора, можна забивати наступні два шаблони для спеціальних прямих трикутників: $45˚$ - $45˚$ - $90˚$ трикутники і $30˚$ - $60˚$ - $90˚$ трикутники.

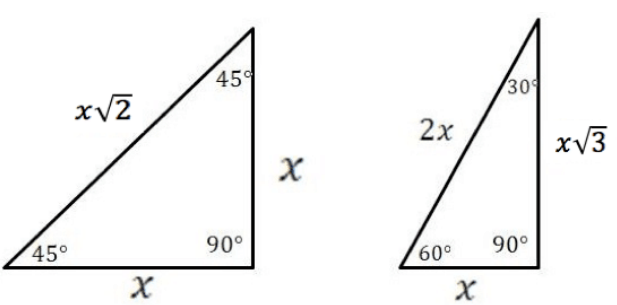
$clipboard_e2026a8b9c765a82686d89e448e76dfa7.png$

Оскільки прямі трикутники і кола нерозривно пов'язані один з одним, гострі кути $30˚$ $45˚$ , часто $60˚$ корисні для знаходження точних значень в тригонометрії; ці рішення не вимагають використання калькулятора.

Приклади спеціальних прямих трикутників і їх рішення, можна подивитися в цих відео:

Спробуйте! (Вправи)

Для #1 -5 намалюйте кут $\theta$ у стандартному положенні.

$\theta = 210˚$
$\theta = −300˚$
$\theta = 150˚$
$\theta = 270˚$
$\theta = −135˚$

Для #6 -10 вкажіть будь-які два кути співтермінал із заданим кутом $\theta$ . Дайте один позитивний котермінальний кут і один негативний котермінальний кут.

$\theta = 30˚$
$\theta = 60˚$
$\theta = 90˚$
$\theta = 180˚$
$\theta = 240˚$

Для #11 -15 вкажіть рівняння кола із заданим радіусом.

$r = 4$
$r = \dfrac{1}{2}$
$r = 3 \sqrt{2}$
$r = \dfrac{\sqrt{6}}{2}$
$r = \sqrt{\dfrac{101}{62}}$
Заповніть пробіли: Одиничне коло - це коло, $\underline{\;\;\;\;\;\;\;\;\;\;}$ рівне одній одиниці. Коло зосереджено на $\underline{\;\;\;\;\;\;\;\;\;\;}$ . Коло має рівняння: $\underline{\;\;\;\;\;\;\;\;\;\;}$ .

Для #17 -24, Задана точка лежить на колі із заданим радіусом та кінцевою стороною у заданому квадранті. Знайти відсутню координату заданої впорядкованої пари.

Точка на колі	Радіус	Квадрант, в якому $\theta$ закінчується.
17. $(2, y)$	$r = 5$	\ (\ тета\) закінчується.» > $\theta ∈$ ЦИ
18. $(x, \sqrt{6})$	$r = 3$	\ (\ тета\) закінчується.» > $\theta ∈$ QII
19. $(−3\sqrt{7}, y)$	$r = \sqrt{77}$	\ (\ тета\) закінчується.» > $\theta ∈$ ІІІ квартал
20. $(x, −4\sqrt{5})$	$r = 3\sqrt{15}$	\ (\ тета\) закінчується.» > $\theta ∈$ QIV
21. $\left( \dfrac{3}{4} , y \right)$	$r=1$	\ (\ тета\) закінчується.» > $\theta ∈$ ЦИ
22. $\left(x, \dfrac{3}{16} \right)$	$r=1$	\ (\ тета\) закінчується.» > $\theta ∈$ QII
23. $\left(− \dfrac{\sqrt{5}}{4} , y \right)$	$r=1$	\ (\ тета\) закінчується.» > $\theta ∈$ ІІІ квартал
24. $\left(x, − \dfrac{3\sqrt{2}}{8} \right)$	$r=1$	\ (\ тета\) закінчується.» > $\theta ∈$ QIV

Для #25 -29 знайдіть частку повного обороту. Потім накидайте кут.

$\dfrac{1}{4} \cdot 360˚$
$\dfrac{1}{2} \cdot 360˚$
$\dfrac{3}{4} \cdot 360˚$
$\dfrac{1}{8} \cdot 360˚$
$\dfrac{1}{6} \cdot 360˚$

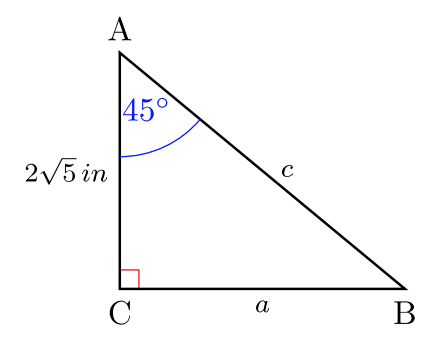
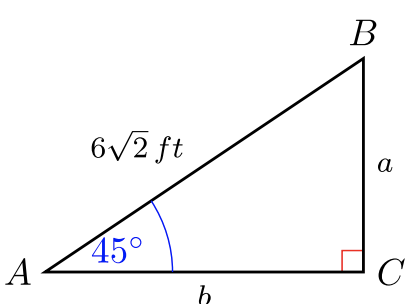
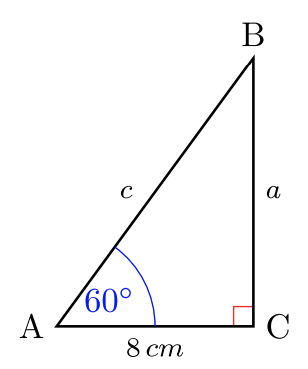
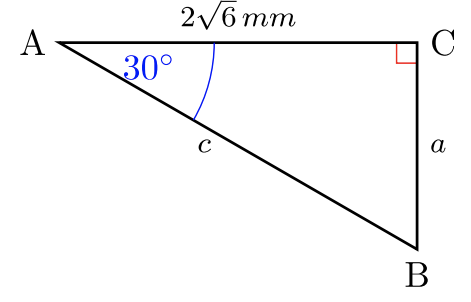
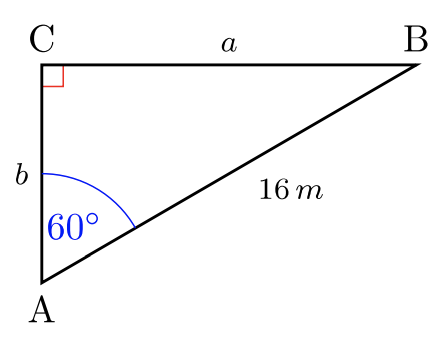
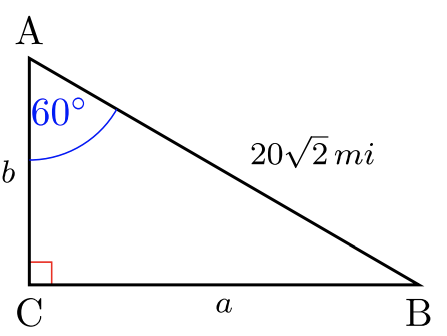
Для #30 -35 вирішіть для $2$ відсутніх довжин сторін. Дайте точні відповіді. Немає калькуляторів.

$clipboard_e71a8a05bff7f6a4adc6d5c0b056fc1d7.png$
$clipboard_ea175eae65ac9e1641c5bbb8d43439f80.png$
$clipboard_ee446e4e95939c7b67716b36c685644d0.png$
$clipboard_e4633229195d2f71629d883fc6a786904.png$
$clipboard_eba2b6dd1020f7ca98f12ad724d338ec6.png$
$clipboard_e5992c086b12706b09765a4a75c4285a0.png$

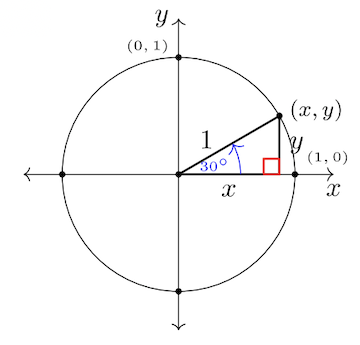
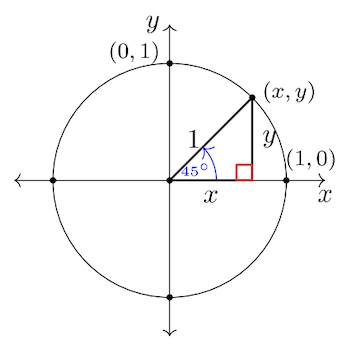
Для #36 -38 знайти координати впорядкованої пари $(x, y)$ на одиничному колі з заданим стандартним кутом. Використовуйте спеціальні зв'язки прямокутного трикутника. Дайте точні значення $x$ і $y$ .

$clipboard_ea02e11ad76d1b60bcb971065f6a9a1eb.png$
$clipboard_ea2c96607cc16568bd33c44e3cc4275ff.png$
$clipboard_e5da8266361bae60ea0067b4ebef91a12.png$