5.7: Раціональні функції

Last updated
Save as PDF

Page ID: 59595

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Використовуйте стрілочні позначення.
Вирішувати прикладні завдання, що включають раціональні функції.
Знайти області раціональних функцій.
Визначте вертикальні асимптоти.
Визначте горизонтальні асимптоти.
Графік раціональних функцій.

Припустимо, ми знаємо, що вартість виготовлення виробу залежить від кількості найменувань$x$, вироблених. Це задається рівнянням$C (x)=15,000x−0.1x^2+1000.$ Якщо ми хочемо знати середню вартість виробництва$x$ предметів, ми розділимо функцію витрат на кількість елементів,$x$. Функція середньої вартості, яка дає середню вартість за одиницю продукції,$x$ що випускається, становить

\[f(x)=\dfrac{15,000x−0.1x^2+1000}{x} \nonumber\]

Багато інших прикладних проблем вимагають знайти середнє значення аналогічним чином, даючи нам змінні в знаменнику. Записується без змінної в знаменнику, ця функція буде містити від'ємне ціле значення.

В останніх кількох розділах ми працювали з поліноміальними функціями, які є функціями з невід'ємними цілими числами для експонент. У цьому розділі ми досліджуємо раціональні функції, які мають змінні в знаменнику.

Використання стрілочного позначення

Ми бачили графіки основної реципрокної функції та квадратної зворотної функції з нашого дослідження функцій інструментарію. Вивчіть ці графіки, як показано на малюнку$\PageIndex{1}$, і зверніть увагу на деякі їх особливості.

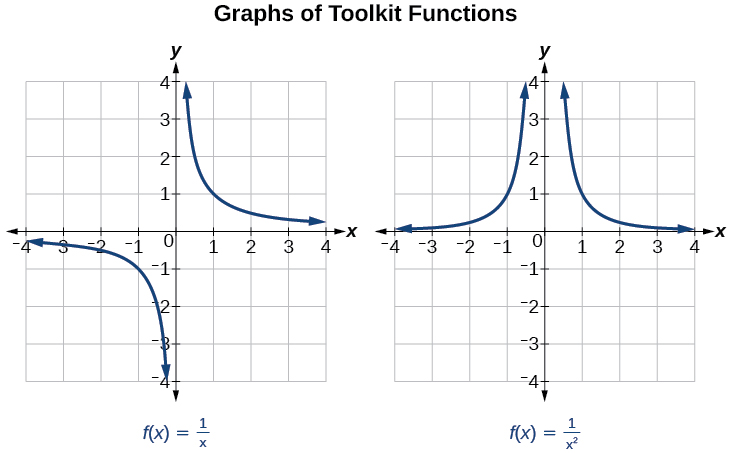
Графіки f (x) = 1/x і f (x) = 1/x^2 — Малюнок$\PageIndex{1}$

Кілька речей очевидні, якщо ми вивчимо графік$f(x)=\frac{1}{x}$.

На лівій гілці графіка крива наближається до$x$ -осі$(y=0)$ як$x\rightarrow -\infty$.
У міру$x = 0$ наближення графіка зліва крива падає, але в міру наближення до нуля справа крива піднімається.
Нарешті, на правій гілці графіка криві наближаються до$x$ -осі$(y=0) $ як$x\rightarrow \infty$.

Підводячи підсумок, ми використовуємо стрілочні позначення, щоб показати, що$x$ або$f (x)$ наближається до певного значення (Таблиця$\PageIndex{1}$).

Таблиця$\PageIndex{1}$
Символ	Значення
$x\rightarrow a^-$	$x$наближається до а зліва ($x<a$але близько до$a$)
$x\rightarrow a^+$	$x$наближається до а праворуч ($x>a$але близько до$a$)
$x\rightarrow \infty$	$x$наближається нескінченність ($x$збільшується без обмежень)
$x\rightarrow −\infty$	$x$наближається негативна нескінченність ($x$зменшується без обмежень
$f(x)\rightarrow \infty$	вихід наближається до нескінченності (вихід збільшується без обмежень)
$f(x)\rightarrow −\infty$	вихід наближається до негативної нескінченності (вихід зменшується без обмежень)
$f(x)\rightarrow a$	вихід наближається$a$

Локальна поведінка$f(x)=\frac{1}{x}$

Почнемо з погляду на зворотну функцію,$f(x)=\frac{1}{x}$. Ми не можемо розділити на нуль, що означає, що функція невизначена в$x=0$; тому нуль не знаходиться в області. У міру наближення вхідних значень з лівого боку до нуля (стають дуже малими, від'ємні значення), значення функції зменшуються без обмежень (іншими словами, наближаються до негативної нескінченності). Ми можемо побачити таку поведінку в табл$\PageIndex{2}$.

Таблиця$\PageIndex{2}$
$x$	—0.1	—0,01	—0,001	—0,0001
$f(x)=\frac{1}{x}$	—10	—100	—1000	—10 000

Пишемо стрілками позначення

як$x\rightarrow 0^−,f(x)\rightarrow −\infty$

Оскільки вхідні значення наближаються до нуля з правого боку (стають дуже маленькими, позитивними значеннями), значення функції збільшуються без обмежень (наближається до нескінченності). Ми можемо побачити таку поведінку в табл$\PageIndex{3}$.

Таблиця$\PageIndex{3}$
$x$	0.1	0,01	0,001	0,0001
$f(x)=\frac{1}{x}$	10	100	1000	10 000

Пишемо стрілками позначення

Як$x\rightarrow 0^+, f(x)\rightarrow \infty$.

Див$\PageIndex{2}$. Малюнок.

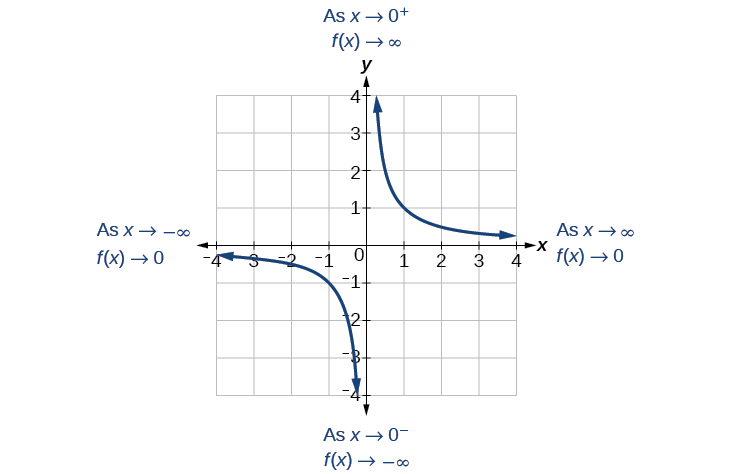
Графік f (x) =1/x, який позначає поведінку кінця. Коли х переходить до негативної нескінченності, f (x) переходить до 0, а як х переходить до 0^-, f (x) переходить до негативної нескінченності. Коли х переходить до позитивної нескінченності, f (x) переходить до 0, а як x переходить до 0 ^ +, f (x) переходить до позитивної нескінченності. — Малюнок$\PageIndex{2}$.

Така поведінка створює вертикальну асимптоту, яка є вертикальною лінією, до якої графік наближається, але ніколи не перетинає. У цьому випадку графік наближається до вертикальної лінії,$x=0$ оскільки вхід стає близьким до нуля (рис.$\PageIndex{3}$).

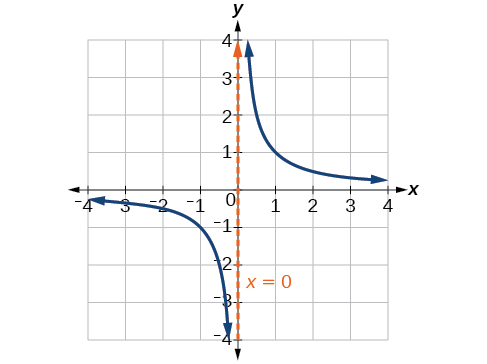
Графік f (x) = 1/x з його вертикальною асимптотою при x=0. — Малюнок$\PageIndex{3}$.

Визначення: ВЕРТИКАЛЬНА АСИМПТОТА

Вертикальна асимптота графіка - це вертикальна лінія,$x=a$ де графік прагне до позитивної або негативної нескінченності у міру наближення входів$a$. пишемо

Як$x\rightarrow a$$f(x)\rightarrow \infty$, або як$x\rightarrow a$,$f(x)\rightarrow −\infty$.

Кінцева поведінка$f(x)=\frac{1}{x}$

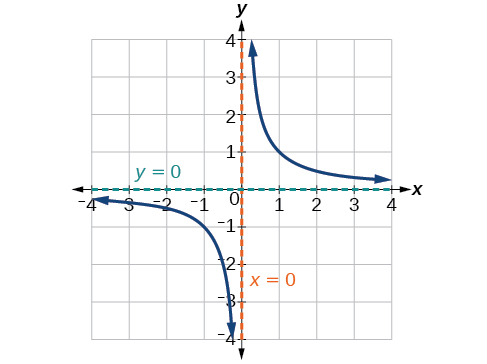
У міру$x$ наближення значень нескінченності наближаються значення функції$0$. У міру$x$ наближення значень негативної нескінченності наближаються значення функції$0$ (рис.$\PageIndex{4}$). Символічно, використовуючи позначення стрілок

Як$x\rightarrow \infty$$f(x)\rightarrow 0$, і як$x\rightarrow −\infty$,$f(x)\rightarrow 0$.

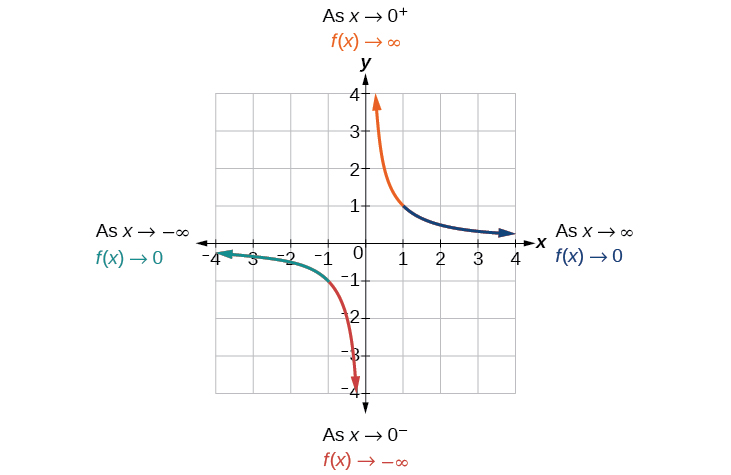
Графік f (x) =1/x, який виділяє сегменти поворотних точок, щоб позначити їх кінцеву поведінку. — Малюнок$\PageIndex{4}$.

Виходячи з цієї загальної поведінки та графіка, ми можемо побачити, що функція наближається до 0, але ніколи насправді не досягає 0; здається, вирівнюється, коли входи стають великими. Така поведінка створює горизонтальну асимптоту, горизонтальну лінію, до якої графік наближається, коли вхідні дані збільшуються або зменшуються без обмежень. При цьому графік наближається до горизонтальної лінії$y=0$. Див$\PageIndex{5}$. Малюнок.

Графік f (x) = 1/x з його вертикальною асимптотою при x = 0 та горизонтальною асимптотою при y = 0. — Малюнок$\PageIndex{5}$.

Визначення: ГОРИЗОНТАЛЬНА АСИМПТОТА

Горизонтальна асимптота графіка - це горизонтальна лінія,$y=b$ де графік наближається до лінії, коли вхідні дані збільшуються або зменшуються без обмежень. пишемо

Як$x\rightarrow \infty \text{ or } x\rightarrow −\infty$,$f(x)\rightarrow b$.

Приклад$\PageIndex{1}$: Using Arrow Notation.

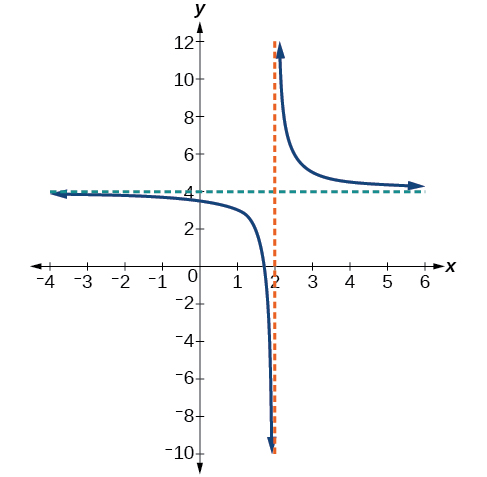
Використовуйте позначення стрілок, щоб описати поведінку кінця та локальну поведінку функції, зображеної на малюнку$\PageIndex{6}$.

Графік f (x) =1/ (x-2) +4 з його вертикальною асимптотою на x=2 та горизонтальною асимптотою при y=4. — Малюнок$\PageIndex{6}$.

Рішення

Зверніть увагу, що графік показує вертикальну асимптоту в$x=2$, який говорить нам, що функція невизначена в$x=2$.

Як$x\rightarrow 2^−$,$f(x)\rightarrow −\infty,$ і як$x\rightarrow 2^+$,$f(x)\rightarrow \infty$.

І як входи зменшуються без обмежень, графік, здається, вирівнюється при вихідних значеннях$4$, вказуючи на горизонтальну асимптоту в$y=4$. Оскільки входи збільшуються без обмежень, рівень графіка вимкнений на$4$.

Як$x\rightarrow \infty$,$f(x)\rightarrow 4$ і як$x\rightarrow −\infty$,$f(x)\rightarrow 4$.

Вправи$\PageIndex{1}$

Використовуйте позначення стрілок, щоб описати поведінку кінця та локальну поведінку для зворотної функції у квадраті.

Відповідь

Кінцева поведінка: як$x\rightarrow \pm \infty$,$f(x)\rightarrow 0$;

Локальна поведінка: as$x\rightarrow 0$,$f(x)\rightarrow \infty$ (немає x- або y-перехоплень)

Приклад$\PageIndex{2}$: Using Transformations to Graph a Rational Function.

Намалюйте графік зворотної функції, зміщеної на дві одиниці вліво і вгору на три одиниці. Визначте горизонтальні та вертикальні асимптоти графіка, якщо такі є.

Рішення

Зсув графіка вліво 2 і вгору 3 призведе до функції

\[f(x)=\dfrac{1}{x+2}+3\]

або еквівалентно, надаючи термінам спільний знаменник,

\[f(x)=\dfrac{3x+7}{x+2}\]

Графік зсунутою функції відображається на малюнку$\PageIndex{7}$.

Графік f (x) =1/ (x+2) +3 з його вертикальною асимптотою на x=-2 та горизонтальною асимптотою при y=3. — Малюнок$\PageIndex{7}$.

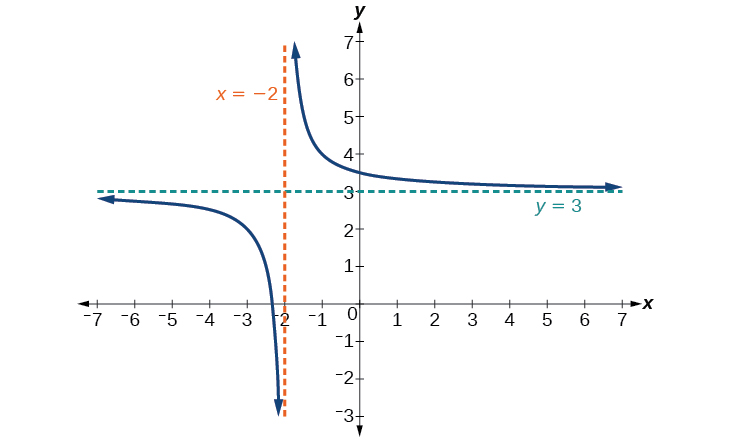
Зверніть увагу, що ця функція не визначена в$x=−2$, і графік також показує вертикальну асимптоту в$x=−2$.

Як$x\rightarrow −2^−$$f(x)\rightarrow −\infty$, і як$x\rightarrow −2^+$,$f(x)\rightarrow \infty$.

Оскільки входи збільшуються та зменшуються без обмежень, графік, здається, вирівнюється при вихідних значеннях 3, що вказує на горизонтальну асимптоту$y=3$.

Як$x\rightarrow \pm \infty$,$f(x)\rightarrow 3$.

Аналіз

Зверніть увагу, що горизонтальні і вертикальні асимптоти зсуваються вліво 2 і вгору 3 разом з функцією.

Вправа$\PageIndex{2}$

Намалюйте графік та знайдіть горизонтальні та вертикальні асимптоти зворотної квадратної функції, яка була зрушена вправо на 3 одиниці та вниз на 4 одиниці.

Рішення

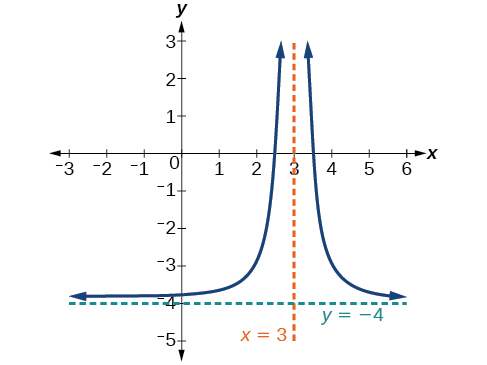
Графік f (x) =1/ (x-3) ^2-4 з його вертикальною асимптотою на x = 3 та горизонтальною асимптотою при y = -4. — Малюнок$\PageIndex{8}$.

Функція і асимптоти зміщені на 3 одиниці вправо і 4 одиниці вниз. Як$x\rightarrow 3$, $f(x)\rightarrow \infty$, and as $x\rightarrow \pm \infty$, $f(x)\rightarrow −4$.

Функція є$f(x)=\frac{1}{{(x−3)}^2}−4$.

Рішення прикладних задач із залученням раціональних функцій

У прикладі$\PageIndex{2}$ ми зрушили функцію інструментарію таким чином, що призвело до функції$f(x)=\frac{3x+7}{x+2}$. Це приклад раціональної функції. Раціональна функція - це функція, яку можна записати як частку двох поліноміальних функцій. Багато реальних проблем вимагають від нас знайти співвідношення двох поліноміальних функцій. Проблеми, пов'язані зі ставками та концентраціями, часто включають раціональні функції.

Визначення: РАЦІОНАЛЬНА ФУНКЦІЯ

Раціональна функція - це функція, яка може бути записана як частка двох поліноміальних функцій$P(x)$ і$Q(x)$.

\[f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0\]

Приклад$\PageIndex{3}$: Solving an Applied Problem Involving a Rational Function

Великий змішувальний бак в даний час містить 100 галонів води, в яку змішали 5 фунтів цукру. Відкриється кран, наливаючи в бак 10 галонів води в хвилину, при цьому в ємність засипається цукор зі швидкістю 1 фунт в хвилину. Знайдіть концентрацію (фунтів на галон) цукру в резервуарі через 12 хвилин. Це більша концентрація, ніж на початку?

Рішення

Нехай t буде кількість хвилин з моменту відкриття крана. Оскільки вода збільшується зі швидкістю 10 галонів в хвилину, а цукор збільшується зі швидкістю 1 фунт в хвилину, це постійні темпи змін. Це говорить нам про те, що кількість води в резервуарі змінюється лінійно, як і кількість цукру в резервуарі. Ми можемо написати рівняння незалежно для кожного:

вода:$W(t)=100+10t$ в галонів

цукор:$S(t)=5+1t$ в фунтах

Концентрація$C$, буде співвідношенням фунтів цукру до галонів води

\[C(t)=\dfrac{5+t}{100+10t}\]

Концентрація через 12 хвилин дається шляхом оцінки$C(t)$ при$t= 12$.

\[\begin{align} C(12) & =\dfrac{5+12}{100+10(12)} \\ &= \dfrac{17}{220} \end{align} \]

Це означає, що концентрація становить 17 фунтів цукру до 220 галонів води.

На початку концентрація становить

\[\begin{align} C(0) & =\dfrac{5+0}{100+10(0)} \\ & =\dfrac{1}{20} \end{align} \]

Так як$\frac{17}{220}≈0.08>\frac{1}{20}=0.05$ концентрація більше через 12 хвилин, ніж на початку.

Аналіз

Щоб знайти горизонтальну асимптоту, ділимо провідний коефіцієнт в чисельнику на провідний коефіцієнт в знаменнику:

\[\dfrac{1}{10}=0.1\]

Зверніть увагу на горизонтальну асимптоту$y= 0.1.$ Це означає, що$C,$ концентрація, співвідношення фунтів цукру до галонів води, наблизиться до 0,1 в довгостроковій перспективі.

Вправа$\PageIndex{3}$

Є 1200 першокурсників і 1500 другокурсників на підготовчому мітингу опівдні. Після 12:00 на мітинг прибувають 20 першокурсників кожні п'ять хвилин, а 15 другокурсників залишають мітинг. Знайти співвідношення першокурсників до другокурсників о 13:00.

Відповідь: $\frac{12}{11}$

Пошук областей раціональних функцій

Вертикальна асимптота представляє значення, при якому раціональна функція невизначена, так що значення не знаходиться в області функції. Зворотна функція не може мати значень у своїй області, які призводять до того, що знаменник дорівнює нулю. Загалом, щоб знайти область раціональної функції, нам потрібно визначити, які входи викликали б поділ на нуль.

Визначення: ДОМЕН РАЦІОНАЛЬНОЇ ФУНКЦІЇ

Область раціональної функції включає в себе всі дійсні числа, крім тих, які викликають значення знаменника рівним нулю.

Як: З огляду на раціональну функцію, знайдіть домен.

Встановіть знаменник, рівний нулю.
Вирішіть, щоб знайти значення x, які призводять до того, що знаменник дорівнює нулю.
Домен - це всі дійсні числа, крім тих, які знайдені на кроці 2.

Приклад$\PageIndex{4}$: Finding the Domain of a Rational Function

Знайдіть домен домену$f(x)=\dfrac{x+3}{x^2−9}$.

Рішення

Почніть з установки знаменника, рівного нулю, і рішення.

\[x^2-9=0 \nonumber \]

\[x^2=9 \nonumber \]\[x=\pm 3 \nonumber \]

Знаменник дорівнює нулю при$x=\pm 3$. Доменом функції є всі дійсні числа, крім$x=\pm 3$.

Аналіз

Графік цієї функції, як показано на малюнку$\PageIndex{9}$, підтверджує, що функція не визначена при$x=\pm 3$.

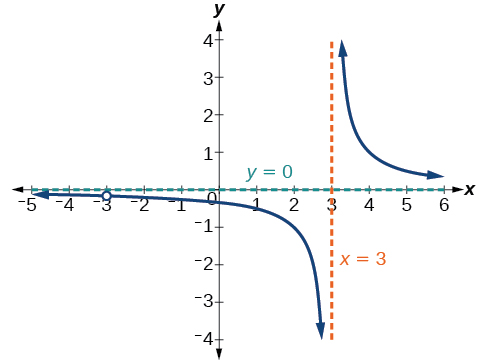
Графік f (x) =1/ (x-3) з його вертикальною асимптотою на x = 3 та горизонтальною асимптотою при y=0. — Малюнок$\PageIndex{9}$.

Існує вертикальна асимптота at$x=3$ і дірка на графіку в$x=−3$. Ці типи отворів ми докладніше обговоримо далі в цьому розділі.

Вправа$\PageIndex{4}$

Знайдіть домен домену$f(x)=\dfrac{4x}{5(x−1)(x−5)}$.

Відповідь: Домен - це всі дійсні числа, крім$x=1$ і$x=5$.

Ідентифікація вертикальних асимптотів раціональних функцій

Дивлячись на графік раціональної функції, ми можемо дослідити її локальну поведінку і легко побачити, чи є асимптоти. Можливо, ми навіть зможемо приблизити їх розташування. Однак навіть без графіка ми все ще можемо визначити, чи має дана раціональна функція будь-які асимптоти, і обчислити їх розташування.

Вертикальні асимптоти

Вертикальні асимптоти раціональної функції можна знайти, вивчивши фактори знаменника, які не є загальними для множників чисельника. Вертикальні асимптоти виникають у нулів таких факторів.

Як: За допомогою раціональної функції визначити будь-які вертикальні асимптоти її графа

Коефіцієнт чисельника і знаменника.
Зверніть увагу на будь-які обмеження в області функції.
Зменшіть вираз, скасувавши загальні множники в чисельнику і знаменнику.
Зверніть увагу на будь-які значення, які призводять до нульового значення знаменника в цьому спрощеному варіанті. Саме тут виникають вертикальні асимптоти.
Зверніть увагу на будь-які обмеження в домені, де асимптоти не виникають. Це знімні розриви, або «дірки».

Приклад$\PageIndex{5}$: Identifying Vertical Asymptotes

Знайти вертикальні асимптоти графа$k(x)=\dfrac{5+2x^2}{2−x−x^2}$.

Рішення

Спочатку множимо чисельник і знаменник.

\[k(x)=\dfrac{5+2x^2}{2−x−x^2} \nonumber \]

\[=\dfrac{5+2x^2}{(2+x)(1-x)} \nonumber \]

Щоб знайти вертикальні асимптоти, визначаємо, де ця функція буде невизначена, встановивши знаменник рівний нулю:

\[(2+x)(1−x)=0 \nonumber \]

\[x=−2, \; x=1 \nonumber \]

$x=–2$Ні нулі чисельника не$x=1$ є, тому два значення вказують на дві вертикальні асимптоти. Графік на малюнку$\PageIndex{10}$ підтверджує розташування двох вертикальних асимптотів.

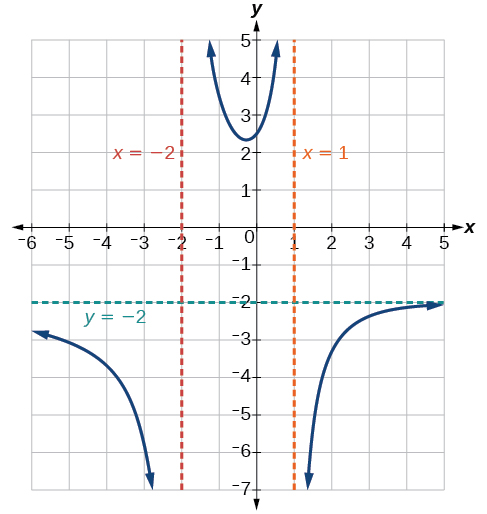
$Графік k (x) = (5+2x) ^2/ (2-x-x^2) з його вертикальними асимптотами при x = -2 та x = 1 та його горизонтальною асимптотою при y = -2.$

Малюнок$\PageIndex{10}$.

Знімні розриви

Іноді графік буде містити дірку: єдину точку, де графік не визначено, позначена відкритим колом. Називаємо такий отвір знімним розривом. Наприклад, функція$f(x)=\dfrac{x^2−1}{x^2−2x−3}$ може бути переписана шляхом факторингу чисельника і знаменника.

\[f(x)=\dfrac{(x+1)(x−1)}{(x+1)(x−3)} \nonumber \]

Зверніть увагу, що$x+1$ є загальним фактором для чисельника та знаменника. Нуль цього фактора$x=−1$, є місцем розташування знімного розриву. Зверніть увагу також, що$ (x–3) $ це не множник як в чисельнику, так і в знаменнику. Нуль цього фактора - вертикальна асимптота.$x=3$ Див$\PageIndex{11}$. Малюнок. [Зауважте, що знімні розриви можуть не бути видимими, коли ми використовуємо калькулятор графіків, залежно від вибраного вікна.]

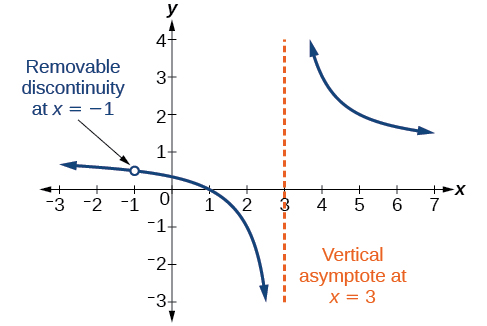
Графік f (x) = (x^2-1)/(x^2-2x-3) з його вертикальною асимптотою при x=3 та знімним розривом при x=-1. — Малюнок$\PageIndex{11}$.

ЗНІМНІ РОЗРИВИ РАЦІОНАЛЬНИХ ФУНКЦІЙ

Знімний розрив відбувається в графі раціональної функції при$x=a$ якщо$a$ дорівнює нулю для множника в знаменнику, який є спільним з множником в чисельнику. Розраховуємо чисельник і знаменник і перевіряємо на загальні фактори. Якщо ми знайдемо будь-який, то ставимо загальний коефіцієнт рівний 0 і вирішуємо. Це місце знімного розриву. Це вірно, якщо кратність цього коефіцієнта більша або дорівнює тому, що в знаменнику. Якщо кратність цього коефіцієнта більше в знаменнику, то при цьому значенні ще існує асимптота.

Приклад$\PageIndex{6}$: Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Знайдіть вертикальні асимптоти та знімні розриви графа$k(x)=\dfrac{x−2}{x^2−4}$.

Рішення

Коефіцієнт чисельника і знаменника.

\[k(x)=\dfrac{x−2}{(x−2)(x+2)} \nonumber \]

Зверніть увагу, що в чисельнику і знаменнику є загальний коефіцієнт,$x–2$. Нуль для цього фактора дорівнює$x=2$. Це місце знімного розриву.

Зверніть увагу, що в знаменнику є коефіцієнт, якого немає в чисельнику,$x+2$. Нуль для цього фактора дорівнює$x=−2$. Вертикальна асимптота є$x=−2$. Див$\PageIndex{12}$. Малюнок.

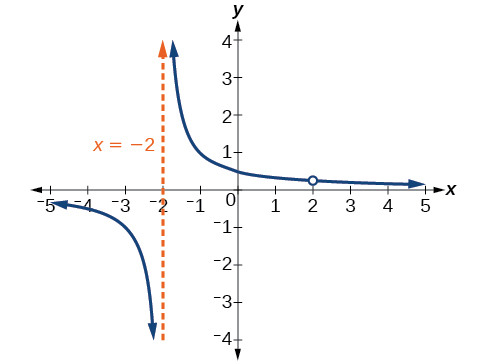
Графік k (x) = (x-2)/(x-2) (x+2) з його вертикальною асимптотою при x=-2 та знімним розривом при x=2. — Малюнок$\PageIndex{12}$.

Графік цієї функції матиме вертикальну асимптоту в$x=−2$, але$x=2$ на графіку буде дірка.

Вправа$\PageIndex{5}$

Знайдіть вертикальні асимптоти та знімні розриви графа$f(x)=\dfrac{x^2−25}{x^3−6x^2+5x}$.

Відповідь

Знімний розрив при$x=5$.

Вертикальні асимптоти:$x=0$,$x=1$.

Ідентифікація горизонтальних асимптотів раціональних функцій

У той час як вертикальні асимптоти описують поведінку графа, оскільки вихід стає дуже великим або дуже малим, горизонтальні асимптоти допомагають описати поведінку графа, оскільки вхідні дані стають дуже великими або дуже малими. Нагадаємо, що кінцева поведінка полінома буде дзеркально відображати поведінку провідного терміна. Так само кінцева поведінка раціональної функції відображатиме співвідношення функції, яке є співвідношенням провідних членів.

Існує три різних результату при перевірці горизонтальних асимптотів:

Випадок 1: Якщо ступінь знаменника > ступінь чисельника, існує горизонтальна асимптота при$y=0$.

Приклад:$f(x)=\dfrac{4x+2}{x^2+4x−5}$

У цьому випадку кінцева поведінка є$f(x)≈\dfrac{4x}{x^2}=\dfrac{4}{x}$. Це говорить нам про те, що, коли входи збільшуються або зменшуються без обмежень, ця функція буде вести себе аналогічно функції$g(x)=\dfrac{4}{x}$, а виходи наближаються до нуля, в результаті чого горизонтальна асимптота при$y=0$. Див$\PageIndex{13}$. Малюнок. Зауважте, що цей графік перетинає горизонтальну асимптоту.

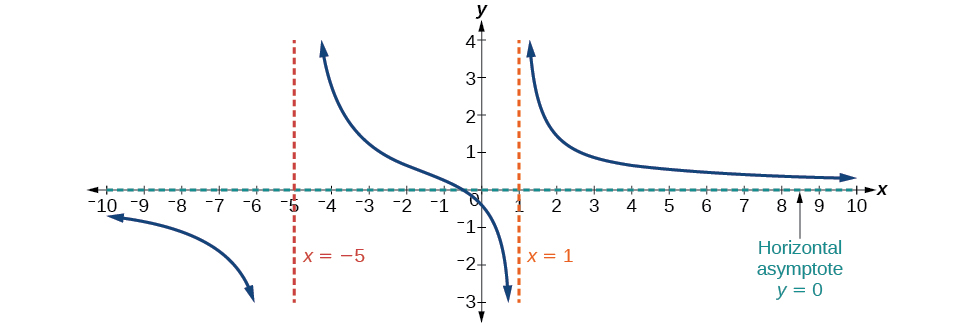
Графік f (x) = (4x+2)/(x^2+4x-5) з його вертикальними асимптотами при x = -5 та x = 1 та його горизонтальною асимптотою при y = 0. — Малюнок$\PageIndex{13}$: Горизонтальна асимптота$y=0$ при$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ де ступінь$p$ < ступінь$q$.

Випадок 2: Якщо ступінь знаменника < ступінь чисельника на одиницю, отримаємо похилу асимптоту.

Приклад:$f(x)=\dfrac{3x^2−2x+1}{x−1}$

У цьому випадку кінцева поведінка є$f(x)≈\dfrac{3x^2}{x}=3x$. Це говорить нам про те, що коли входи збільшуються або зменшуються без обмежень, ця функція буде вести себе подібно до функції$g(x)=3x$. Оскільки входи зростають великими, виходи зростатимуть, а не вирівнюватимуться, тому цей графік не має горизонтальної асимптоти. Однак графік$g(x)=3x$ виглядає як діагональна лінія, а так як$f$ буде вести себе аналогічно$g$, то буде наближатися до лінії, близької до$y=3x$. Ця лінія є похилою асимптотикою.

Щоб знайти рівняння похилої асимптоти, ділимо$\dfrac{3x^2−2x+1}{x−1}$. Коефіцієнт є$3x+1$, а залишок дорівнює 2. Похила асимптота - це графік прямої$g(x)=3x+1$. Див$\PageIndex{14}$. Малюнок.

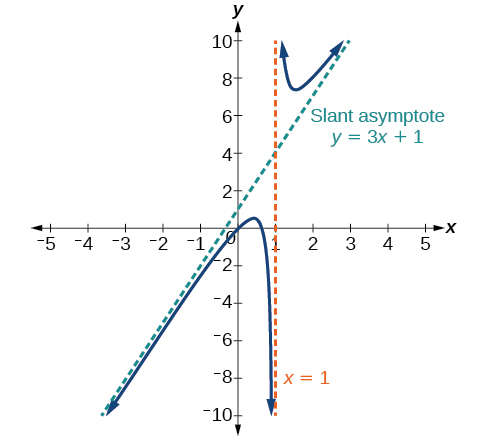
Графік f (x) = (3x^2-2x+1)/(x-1) з його вертикальною асимптотою при x=1 та похилою асимптотою aty=3x+1. — Малюнок$\PageIndex{14}$: Похила асимптота при$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ де$p$ ступінь >ступінь$q$ на 1.

Випадок 3: Якщо ступінь знаменника = ступінь чисельника, існує горизонтальна асимптота при$y=\dfrac{a_n}{b_n}$, де$a_n$ і$b_n$ є відповідно провідними коефіцієнтами$p(x)$ і$q(x)$ for$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$.

Приклад:$f(x)=\dfrac{3x^2+2}{x^2+4x−5}$

У цьому випадку кінцева поведінка є$f(x)≈\dfrac{3x^2}{x^2}=3$. Це говорить нам про те, що у міру збільшення входів ця функція буде вести себе як функція$g(x)=3$, яка є горизонтальною лінією. Як$x\rightarrow \pm \infty$$f(x)\rightarrow 3$, в результаті чого виникає горизонтальна асимптота при$y=3$. Див$\PageIndex{15}$. Малюнок. Зауважте, що цей графік перетинає горизонтальну асимптоту.

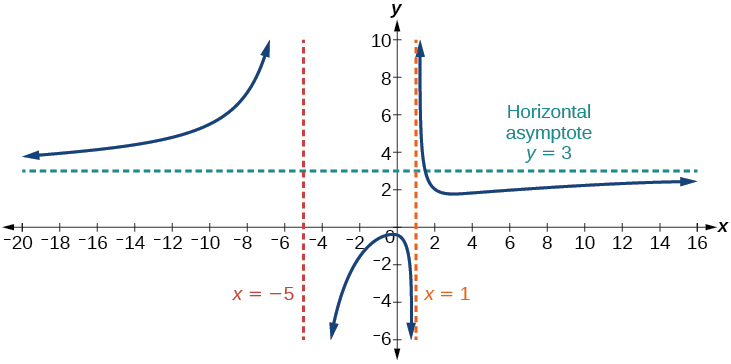
Графік f (x) = (3x^2+2)/(x^2+4x-5) з його вертикальними асимптотами при x = -5 та x = 1 та його горизонтальною асимптотою при y = 3. — Малюнок$\PageIndex{15}$: Горизонтальна асимптота при$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ де ступінь$p$ = ступінь$q$.

Зверніть увагу, що, хоча графік раціональної функції ніколи не перетинає вертикальну асимптоту, графік може або не може перетинати горизонтальну або похилу асимптоту. Крім того, хоча графік раціональної функції може мати багато вертикальних асимптотів, графік матиме не більше однієї горизонтальної (або похилої) асимптоти.

Слід зазначити, що, якщо ступінь чисельника більше ступеня знаменника більше ніж на одиницю, кінцева поведінка графа буде імітувати поведінку скороченого дробу кінцевої поведінки. Наприклад, якщо у нас була функція

\[f(x)=\dfrac{3x^5−x^2}{x+3} \nonumber \]

з поведінкою кінця

\[f(x)≈\dfrac{3x^5}{x}=3x^4 \nonumber \]

кінцева поведінка графіка буде схожа на поведінку парного полінома з позитивним провідним коефіцієнтом.

$x\rightarrow \pm \infty, f(x)\rightarrow \infty$

ГОРИЗОНТАЛЬНІ АСИМПТОТИ РАЦІОНАЛЬНИХ ФУНКЦІЙ

Горизонтальну асимптоту раціональної функції можна визначити, дивлячись на ступені чисельника і знаменника.

Ступінь чисельника менше ступеня знаменника: горизонтальна асимптота при$y=0$.
Ступінь чисельника більше ступеня знаменника на одиницю: немає горизонтальної асимптоти; похила асимптота.
Ступінь чисельника дорівнює ступеня знаменника: горизонтальна асимптота при співвідношенні провідних коефіцієнтів.

Приклад$\PageIndex{7}$: Identifying Horizontal and Slant Asymptotes

Для перерахованих функцій визначте горизонтальну або похилу асимптоту.

$g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}$
$h(x)=\dfrac{x^2−4x+1}{x+2}$
$k(x)=\dfrac{x^2+4x}{x^3−8}$

Рішення

Для цих рішень ми і будемо використовувати$f(x)=\dfrac{p(x)}{q(x)},\space q(x)≠0$.

$g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}$:$p = $ Ступінь ступеня$q=3$, тому ми можемо знайти горизонтальну асимптоту, взявши співвідношення провідних членів. Виникає горизонтальна асимптота при$y =\frac{6}{2}$ або$y=3$.
$h(x)=\dfrac{x^2−4x+1}{x+2}$: Ступінь$p=2$ і ступінь$q=1$. Так як$p>q$ на 1, існує похила асимптота, виявлена при$\dfrac{x^2−4x+1}{x+2}$.
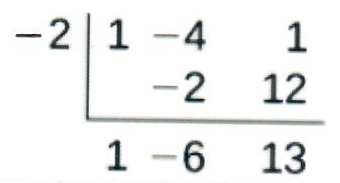
$clipboard_e5ff4f00a1466e92caa3ddac0dac32f5b.png$
$k(x)=\dfrac{x^2+4x}{x^3−8}$: Ступінь$p=2$ < ступінь$q=3$, тому існує горизонтальна асимптота$y=0$.

Приклад$\PageIndex{8}$ Identifying Horizontal Asymptotes

У задачі концентрації цукру раніше ми створили рівняння$C(t)=\dfrac{5+t}{100+10t}$.

Знайдіть горизонтальну асимптоту та інтерпретуйте її в контексті задачі.

Рішення

І чисельник, і знаменник лінійні (ступінь 1). Оскільки градуси рівні, буде горизонтальна асимптота при співвідношенні провідних коефіцієнтів. У чисельнику провідним є член$t$, з коефіцієнтом 1. У знаменнику провідний член - 10t, з коефіцієнтом 10. Горизонтальна асимптота буде при співвідношенні цих значень:

$t\rightarrow \infty,\space C(t)\rightarrow \frac{1}{10}$

Ця функція матиме горизонтальну асимптоту при$y=\frac{1}{10}$.

Це говорить нам про те, що зі$t$ збільшенням значень наближаються значення$C$ волі$\frac{1}{10}$. У контексті це означає, що, як проходить більше часу, концентрація цукру в резервуарі наблизиться до однієї десятої фунта цукру на галон води або$\frac{1}{10}$ фунтів на галон.

Приклад$\PageIndex{9}$: Identifying Horizontal and Vertical Asymptotes

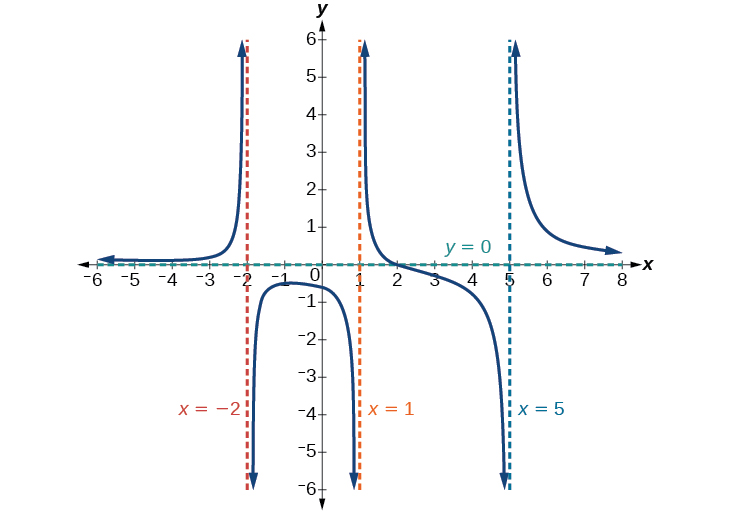
Знайти горизонтальний і вертикальний асимптоти функції$f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}$

Рішення

По-перше, зверніть увагу, що ця функція не має загальних факторів, тому потенційних знімних розривів немає.

Функція матиме вертикальні асимптоти, коли знаменник дорівнює нулю, внаслідок чого функція буде невизначена. Знаменником буде нуль при$x=1,–2,$ і$5$, що вказує на вертикальні асимптоти при цих значеннях.

Чисельник має ступінь$2$, тоді як знаменник має ступінь 3. Оскільки ступінь знаменника більше, ніж ступінь чисельника, знаменник буде рости швидше, ніж чисельник, внаслідок чого виходи прагнуть до нуля, оскільки входи стають великими, і так як$x\rightarrow \pm \infty$,$f(x)\rightarrow 0$. Ця функція матиме горизонтальну асимптоту на$y =0.$ Див$\PageIndex{16}$. Рисунок.

Графік f (x) = (x-2) (x+3)/(x-1) (x+2) (x-2) (x-5) з його вертикальними асимптотами при x = -2, x = 1 та x = 5 та горизонтальній асимптоті при y = 0. — Малюнок$\PageIndex{16}$.

Вправа$\PageIndex{6}$

Знайдіть вертикальний і горизонтальний асимптоти функції:

$f(x)=\dfrac{(2x−1)(2x+1)}{(x−2)(x+3)}$

Відповідь

Вертикальні асимптоти при$x=2$ і$x=–3$

горизонтальна асимптота при$y =4$.

ПЕРЕХОПЛЕННЯ РАЦІОНАЛЬНИХ ФУНКЦІЙ

Раціональна функція матиме$y$ -intercept at,$f(0),$ якщо функція визначена на нулі. Раціональна функція не матиме$y$ -intercept, якщо функція не визначена на нулі.

Аналогічно, раціональна функція матиме$x$ -перехоплення на входах, які призводять до нульового значення виходу. Оскільки дріб дорівнює нулю тільки тоді, коли чисельник дорівнює нулю, x-перехоплення можуть відбуватися тільки тоді, коли чисельник раціональної функції дорівнює нулю.

Приклад$\PageIndex{10}$: Finding the Intercepts of a Rational Function

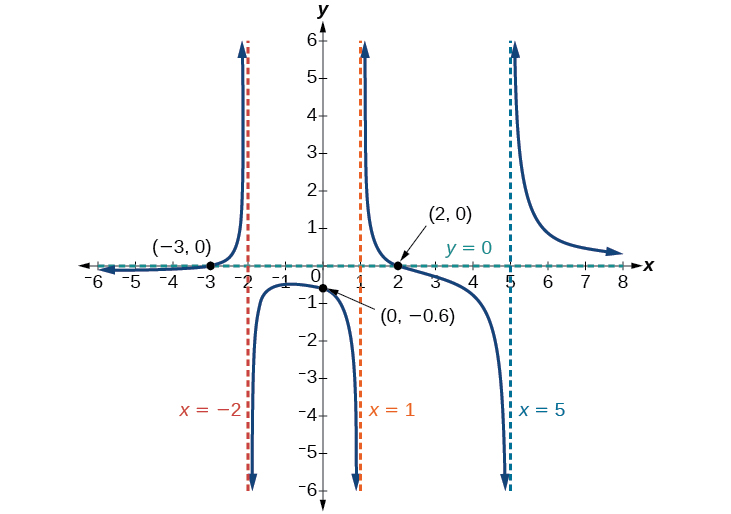
Знайти перехоплення $f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}$.

Рішення

Ми можемо знайти y-перехоплення, оцінивши функцію на нулі

$f(0)=\dfrac{(0−2)(0+3)}{(0−1)(0+2)(0−5)}$

$=−\dfrac{6}{10}$

$=−\dfrac{3}{5}$

$=−0.6$

X-перехоплення відбуватимуться, коли функція дорівнює нулю:

\[ 0=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)} \text{ This is zero when the numerator is zero.} \nonumber \]

\[ 0=(x−2)(x+3) \qquad \qquad \qquad \qquad \qquad \nonumber \]

\[ x=2, x=−3 \qquad \qquad \qquad \qquad \qquad \nonumber \]

Y-перехоплення є$(0,–0.6)$, Х-перехоплення є$(2,0)$ і$(–3,0)$. Див$\PageIndex{17}$. Малюнок.

Графік f (x) = (x-2) (x+3)/(x-1) (x+2) (x-5) з його вертикальними асимптотами при x = -2, x = 1 і x = 5, його горизонтальна асимптота при y = 0, і перехоплення в (-3, 0), (0, -0.6) і (2, 0). — Малюнок$\PageIndex{17}$.

Вправа$\PageIndex{7}$

З огляду на зворотну квадратну функцію, яка зсувається вправо на 3 одиниці і вниз на 4 одиниці, запишіть це як раціональну функцію. Потім знайдіть x- та y-перехоплення та горизонтальні та вертикальні асимптоти.

Відповідь

Для перетвореної зворотної квадратної функції знайдемо раціональну форму.

$f(x)=\dfrac{1}{{(x−3)}^2}−4=\dfrac{1−4{(x−3)}^2}{{(x−3)}^2}=\dfrac{1−4(x^2−6x+9)}{(x−3)(x−3)}=\dfrac{−4x^2+24x−35}{x^2−6x+9}$

Тому що чисельник такий же ступінь, як знаменник ми знаємо, що як$x\rightarrow \pm \infty$,$f(x)\rightarrow −4$; так$y=–4$ і горизонтальна асимптота. Далі встановлюємо знаменник, рівний нулю, і знаходимо, що вертикальна асимптота є$x=3$, тому що as$x\rightarrow 3$,$f(x)\rightarrow \infty$. Потім ми встановимо чисельник рівний$0$ і знайти х-перехоплення знаходяться в$(2.5,0)$ і$(3.5,0)$. Нарешті, ми оцінюємо функцію в 0 і знаходимо y-перехоплення, щоб бути в$(0,−\frac{35}{9})$.

Графічні раціональні функції

У прикладі ми бачимо$\PageIndex{10}$, що чисельник раціональної функції виявляє x -перехоплення графа, тоді як знаменник виявляє вертикальні асимптоти графа. Як і у випадку з поліномами, множники чисельника можуть мати цілу силу більше одиниці. На щастя, вплив на форму графіка при цих перехопленнях такий же, як ми бачили з поліномами.

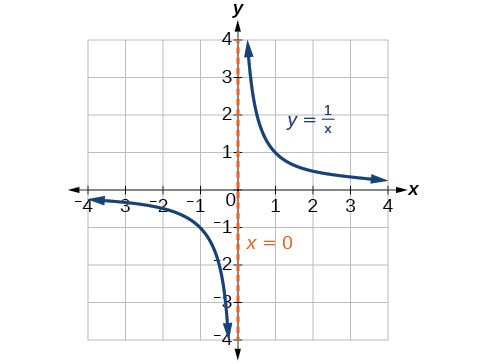
Вертикальні асимптоти, пов'язані з факторами знаменника, відображатимуть одну з двох взаємних функцій інструментарію. Коли ступінь коефіцієнта в знаменнику непарна, відмінною характеристикою є те, що з одного боку вертикальної асимптоти графік спрямовується до позитивної нескінченності, а з іншого боку графік спрямовується до негативної нескінченності. Див$\PageIndex{18}$. Малюнок.

Графік y=1/x з його вертикальною асимптотою при x=0. — Малюнок$\PageIndex{18}$.

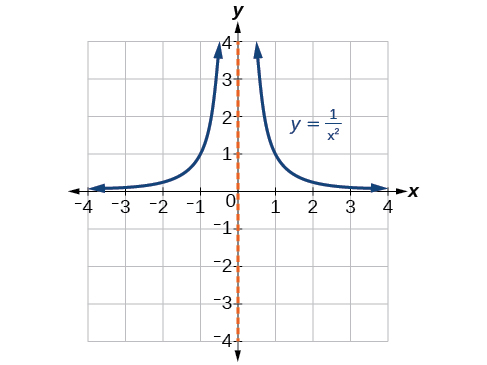
Коли ступінь коефіцієнта в знаменнику парна, відмінною характеристикою є те, що графік або прямує до позитивної нескінченності з обох сторін вертикальної асимптоти, або прямує до негативної нескінченності з обох сторін. Див$\PageIndex{19}$. Малюнок.

Графік y=1/x^2 з його вертикальною асимптотою при x=0. — Малюнок$\PageIndex{19}$.

Наприклад, графік $f(x)=\dfrac{{(x+1)}^2(x−3)}{{(x+3)}^2(x−2)}$показаний на малюнку$\PageIndex{20}$.

Графік f (x) = (x+1) ^2 (x-3)/(x+3) ^2 (x-2) з його вертикальними асимптотами при x = -3 та x = 2, його горизонтальною асимптотою при y = 1 та перехопленнями в (-1, 0), (0, 1/6) та (3, 0). — Малюнок$\PageIndex{20}$.

При х-перехопленні,$x=−1$ відповідному${(x+1)}^2$ множнику чисельника, граф «відскакує», узгоджений з квадратичним характером множника.
При перехопленні x,$x=3$ відповідному$(x−3)$ множнику чисельника, графік проходить через вісь так, як ми очікували від лінійного коефіцієнта.
При вертикальній асимптоті,$x=−3$ відповідній${(x+3)}^2$ множнику знаменника, графік спрямовується до позитивної нескінченності по обидва боки асимптоти, узгодженої з поведінкою функції$f(x)=\dfrac{1}{x^2}$.
При вертикальній асимптоті$x=2$, відповідній$(x−2)$ множнику знаменника, графік направляється до позитивної нескінченності з лівого боку асимптоти і до негативної нескінченності з правого боку, узгодженої з поведінкою функції$f(x)=\dfrac{1}{x}$.

Howto: З огляду на раціональну функцію, намалюйте графік.

Оцінити функцію в 0, щоб знайти y-перехоплення.
Коефіцієнт чисельника і знаменника.
Для множників в чисельнику, не загальних для знаменника, визначте, де кожен множник чисельника дорівнює нулю, щоб знайти х-перехоплення.
Знайдіть кратність x-перехоплень, щоб визначити поведінку графіка в цих точках.
Для факторів в знаменнику зверніть увагу на кратність нулів, щоб визначити локальну поведінку. Для тих факторів, які не є загальними для чисельника, знайдіть вертикальні асимптоти, встановивши ці коефіцієнти, рівні нулю, а потім розв'яжіть.
Для множників у знаменнику, загальних для множників у чисельнику, знайдіть знімні розриви, встановивши ці коефіцієнти, рівні 0, а потім розв'яжіть.
Порівняйте ступені чисельника і знаменника, щоб визначити горизонтальні або похилі асимптоти.
Намалюйте графік.

Приклад$\PageIndex{11}$: Graphing a Rational Function

Намалюйте графік$f(x)=\frac{(x+2)(x−3)}{{(x+1)}^2(x−2)}$.

Рішення

Ми можемо почати з того, що функція вже врахована, заощаджуючи нам крок.

Далі знайдемо перехоплення. Оцінка функції на нулі дає y-перехоплення:

$f(0)=\dfrac{(0+2)(0−3)}{{(0+1)}^2(0−2)}=3$

Щоб знайти x-перехоплення, визначаємо, коли чисельник функції дорівнює нулю. Встановлюючи кожен коефіцієнт рівний нулю, знаходимо x-перехоплення при$x=–2$ і$x=3$. У кожного поведінка буде лінійним (кратність 1), при цьому графік проходить через перехоплення.

У нас є y-перехоплення в$(0,3)$ і х-перехоплює в$(–2,0)$ і$(3,0)$.

Щоб знайти вертикальні асимптоти, визначаємо, коли знаменник дорівнює нулю. Це відбувається, коли$x+1=0$ і коли$x–2=0$, даючи нам вертикальні асимптоти при$x=–1$ і$x=2$.

У чисельнику і знаменнику відсутні загальні фактори. Це означає, що немає знімних розривів.

Нарешті, ступінь знаменника більше, ніж ступінь чисельника, кажучи нам, що цей графік має горизонтальну асимптоту в$y =0$.

Щоб намалювати графік, ми могли б почати з побудови трьох перехоплень. Оскільки графік не має x-перехоплень між вертикальними асимптотами, а y-перехоплення є позитивним, ми знаємо, що функція повинна залишатися позитивною між асимптотами, дозволяючи нам заповнити середню частину графіка, як показано на малюнку$\PageIndex{21}$.

Графік лише середньої частини f (x) = (x+2) (x-3)/(x+1) ^2 (x-2) з його перехопленнями в (-2, 0), (0, 3) і (3, 0). — Малюнок$\PageIndex{21}$.

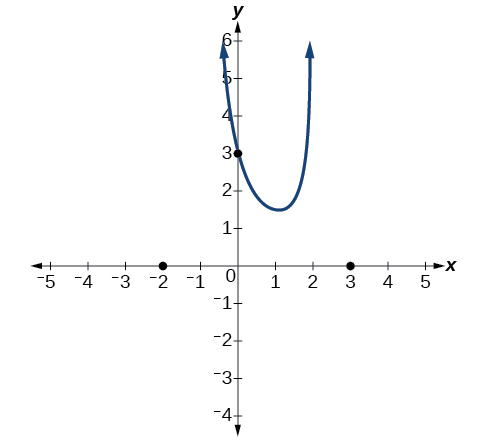
Фактор, пов'язаний з вертикальною$x=−1$ асимптотою в квадраті, тому ми знаємо, що поведінка буде однаковою з обох сторін асимптоти. Графік спрямовується до позитивної нескінченності, оскільки входи наближаються до асимптоти праворуч, тому графік також буде спрямовуватися до позитивної нескінченності зліва.

Для вертикальної асимптоти при$x=2$ коефіцієнт не був квадрат, тому графік матиме протилежну поведінку по обидва боки асимптоти. Див$\PageIndex{22}$. Малюнок. Після проходження через x-перехоплення графік буде вирівнюватися до виходу нуля, як зазначено горизонтальною асимптотою.

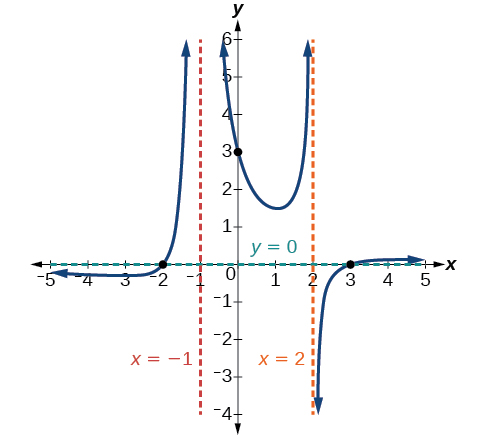
Графік f (x) = (x+2) (x-3)/(x+1) ^2 (x-2) з його вертикальними асимптотами при x = -1 і x = 2, його горизонтальною асимптотою при y = 0 та перехопленнями в (-2, 0), (0, 3) та (3, 0). — Малюнок$\PageIndex{22}$.

Вправа$\PageIndex{8}$

З огляду на функцію$f(x)=\frac{{(x+2)}^2(x−2)}{2{(x−1)}^2(x−3)}$, використовуйте характеристики поліномів і раціональних функцій для опису її поведінки та ескізу функції.

Відповідь

Горизонтальна асимптота в$y=\frac{1}{2}$. Вертикальні асимптоти в$x=1$ а$x=3$. y-перехоплюють в$(0,\frac{4}{3})$.

х перехоплює при$(2,0)$ і$(–2,0)$. $(–2,0)$дорівнює нулю з кратністю$2$, і графік відскакує від осі x в цій точці. $(2,0)$є єдиним нулем, і графік перетинає вісь у цій точці.

Графік f (x) = (x+2) ^2 (x-2) /2 (x-1) ^2 (x-3) з його вертикальним і горизонтальним асимптотами. — Малюнок$\PageIndex{23}$.

Написання раціональних функцій

Тепер, коли ми проаналізували рівняння для раціональних функцій та те, як вони співвідносяться з графіком функції, ми можемо використовувати інформацію, надану графіком, для запису функції. Раціональна функція, записана у факторованій формі, матиме x -перехоплення, де кожен множник чисельника дорівнює нулю. (Виняток виникає в разі знімного розриву.) В результаті ми можемо сформувати чисельник функції, графік якої буде проходити через безліч х -перехоплень шляхом введення відповідної множини факторів. Так само, оскільки функція матиме вертикальну асимптоту, де кожен множник знаменника дорівнює нулю, ми можемо сформувати знаменник, який буде виробляти вертикальні асимптоти, вводячи відповідний набір факторів.

НАПИСАННЯ РАЦІОНАЛЬНИХ ФУНКЦІЙ З ПЕРЕХОПЛЕНЬ І АСИМПТОТІВ

Якщо раціональна функція має x-перехоплення at$x=x_1,x_2,...,x_n$, вертикальні асимптоти at$x=v_1,v_2,…,v_m$$v_j$, а не$x_i=$ будь-які, то функцію можна записати у вигляді:

$f(x)=a\dfrac{ {(x−x_1)}^{p_1} {(x−x_2)}^{p_2}⋯{(x−x_n)}^{p_n} }{ {(x−v_1)}^{q_1} {(x−v_2)}^{q_2}⋯{(x−v_m)}^{q_n}}$

де степені$p_i$ або$q_i$ по кожному фактору можуть бути визначені поведінкою графа при відповідному перехопленні або асимптоті, а коефіцієнт розтягування$a$ може бути визначений за значенням функції, відмінної від x-перехоплення або по горизонтальній асимптоті, якщо вона ненульова.

Задано графік раціональної функції, запишіть функцію.

Визначте фактори чисельника. Вивчіть поведінку графіка на х -перехопленнях, щоб визначити нулі та їх кратність. (Це легко зробити, якщо знайти «найпростішу» функцію з невеликою кратністю, наприклад, 1 або 3, але може бути важко для великих кратностей - наприклад, 5 або 7, наприклад.)
Визначте фактори знаменника. Вивчіть поведінку по обидва боки кожної вертикальної асимптоти, щоб визначити фактори та їх повноваження.
Використовуйте будь-яку чітку точку на графіку, щоб знайти коефіцієнт розтягування.

Приклад$\PageIndex{12}$: Writing a Rational Function from Intercepts and Asymptotes

Напишіть рівняння для раціональної функції, наведеної на малюнку$\PageIndex{24}$.

Графік раціональної функції. — Малюнок$\PageIndex{24}$.

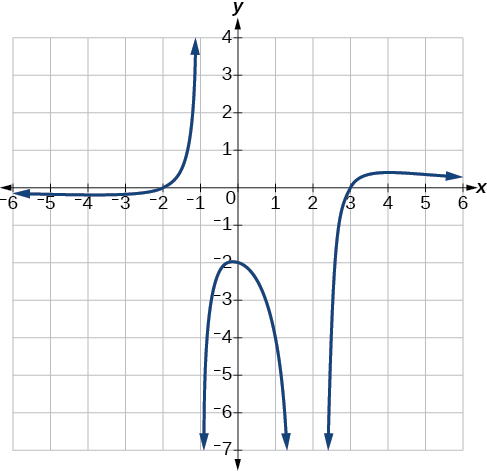
Рішення

Графік, здається, має x-перехоплення в$x=–2$ і$x=3$. На обох графік проходить через перехоплення, припускаючи лінійні фактори. Графік має дві вертикальні асимптоти. Один,$x=–1$ здається, демонструє основну поведінку, подібну до$\dfrac{1}{x}$, з графіком, що рухається до позитивної нескінченності з одного боку і спрямовується до негативної нескінченності з іншого. Асимптота при$x=2$ проявляє поведінку, подібну до$\dfrac{1}{x^2}$, з графіком, що рухається до негативної нескінченності по обидва боки асимптоти. Див$\PageIndex{25}$. Малюнок.

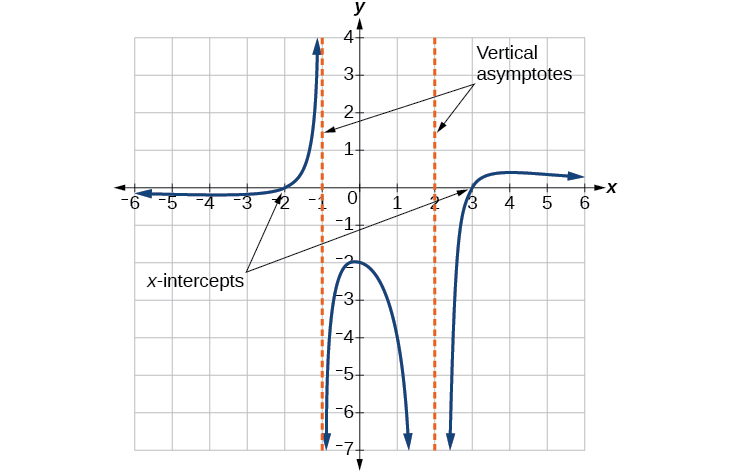
Графік раціональної функції, що позначає її вертикальні асимптоти та x-перехоплення. — Малюнок$\PageIndex{25}$.

Ми можемо використовувати цю інформацію для написання функції форми

$f(x)=a\dfrac{(x+2)(x−3)}{(x+1){(x−2)}^2}$

Щоб знайти коефіцієнт розтягування, ми можемо використовувати іншу чітку точку на графіку, таку як y -перехоплення$(0,–2)$.

$−2=a\dfrac{(0+2)(0−3)}{(0+1){(0−2)}^2}$

$-2=a\dfrac{−6}{4}$

$a=\dfrac{−8}{−6}=\dfrac{4}{3}$

Це дає нам остаточну функцію$f(x)=\dfrac{4(x+2)(x−3)}{3(x+1){(x−2)}^2}$.

Медіа

Отримайте доступ до цих онлайн-ресурсів для додаткового навчання та практики з раціональними функціями.

Ключові рівняння

Раціональна функція$ \qquad $$f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0$

Ключові концепції

Ми можемо використовувати стрілочні позначення для опису локальної поведінки та кінцевої поведінки функцій інструментарію$f(x)=\frac{1}{x}$ та$f(x)=\frac{1}{x^2}$. Див$\PageIndex{1}$. Приклад.
Функція, яка вирівнюється за горизонтальним значенням, має горизонтальну асимптоту. Функція може мати більше однієї вертикальної асимптоти. Див. Приклад.
Проблеми застосування, пов'язані з нормами та концентраціями, часто включають раціональні функції. Див. Приклад.
Область раціональної функції включає в себе всі дійсні числа, крім тих, які викликають значення знаменника рівним нулю. Див. Приклад.
Вертикальні асимптоти раціональної функції виникнуть там, де знаменник функції дорівнює нулю, а чисельник не дорівнює нулю. Див. Приклад.
Знімний розрив може виникнути на графіку раціональної функції, якщо вхідні дані призводять до нулю і чисельника, і знаменника. Див. Приклад.
Кінцева поведінка раціональної функції відображатиме співвідношення провідних членів функцій чисельника та знаменника. Див. Приклад , Приклад , Приклад та Приклад.
Графік раціональних функцій шляхом знаходження перехоплень, поведінки при перехопленнях та асимптотах та поведінці кінця. Див. Приклад.
Якщо раціональна функція має x-перехоплення at$x=x_1,x_2,…,x_n$, вертикальні асимптоти at$x=v_1,v_2,…,v_m$$v_j$, а не$x_i=$ будь-які, то функцію можна записати у вигляді

Символ	Значення
\(x\rightarrow a^-\)	\(x\)наближається до а зліва (\(x<a\)але близько до\(a\))
\(x\rightarrow a^+\)	\(x\)наближається до а праворуч (\(x>a\)але близько до\(a\))
\(x\rightarrow \infty\)	\(x\)наближається нескінченність (\(x\)збільшується без обмежень)
\(x\rightarrow −\infty\)	\(x\)наближається негативна нескінченність (\(x\)зменшується без обмежень
\(f(x)\rightarrow \infty\)	вихід наближається до нескінченності (вихід збільшується без обмежень)
\(f(x)\rightarrow −\infty\)	вихід наближається до негативної нескінченності (вихід зменшується без обмежень)
\(f(x)\rightarrow a\)	вихід наближається\(a\)

\(x\)	—0.1	—0,01	—0,001	—0,0001
\(f(x)=\frac{1}{x}\)	—10	—100	—1000	—10 000

Використання стрілочного позначення

Локальна поведінка\(f(x)=\frac{1}{x}\)

Кінцева поведінка\(f(x)=\frac{1}{x}\)

Рішення прикладних задач із залученням раціональних функцій

Пошук областей раціональних функцій

Ідентифікація вертикальних асимптотів раціональних функцій

Вертикальні асимптоти

Знімні розриви

Ідентифікація горизонтальних асимптотів раціональних функцій

Графічні раціональні функції

Написання раціональних функцій

Ключові рівняння

Ключові концепції