7.3: Радіани

Last updated

Oct 27, 2022
Save as PDF
- 7.2: Довідкові кути
- 8: Вирішення проблем

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Кути можуть вимірюватися в одиницях градусів або радіанах.

Визначення: Радіани

Радіани - це одиниця кутового виміру, визначена таким чином, що

$2\pi \text{ radians } = 360˚$

Для підступних на серце кут $1$ радіана можна створити за допомогою кола (використовувати будь-яку кришку від баночки) і шматочком мотузки.

Рисунок Template:index: Від центру кола відкладіть рядок вниз, щоб створити радіус. Потім обрізаємо мотузку за розміром її радіуса. Рядок міра = радіус вимірювання

Рисунок Template:index: Далі візьміть вирізану рядок і вставте її до краю кола. Центр кола - це вершина кута. Кінцеві точки струн з'єднайте з центром кола. Кут - один радіан!

Нагадаємо, що окружність кола (яка є периметром кола) має формулу:

Окружність = $C = 2 \pi r$ де $r =$ радіус кола

Скільки прядок довжини $r$ потрібно обернути по всьому колу? Ділимо окружність $r$ способами: $\dfrac{2 \pi r}{r} = 2 \pi ≈ 6$ . Про $6$ струни довжини $r$ , або точно $2 \pi$ струни.

Обертання кута проти годинникової стрілки можна виміряти як частку повного обертання.

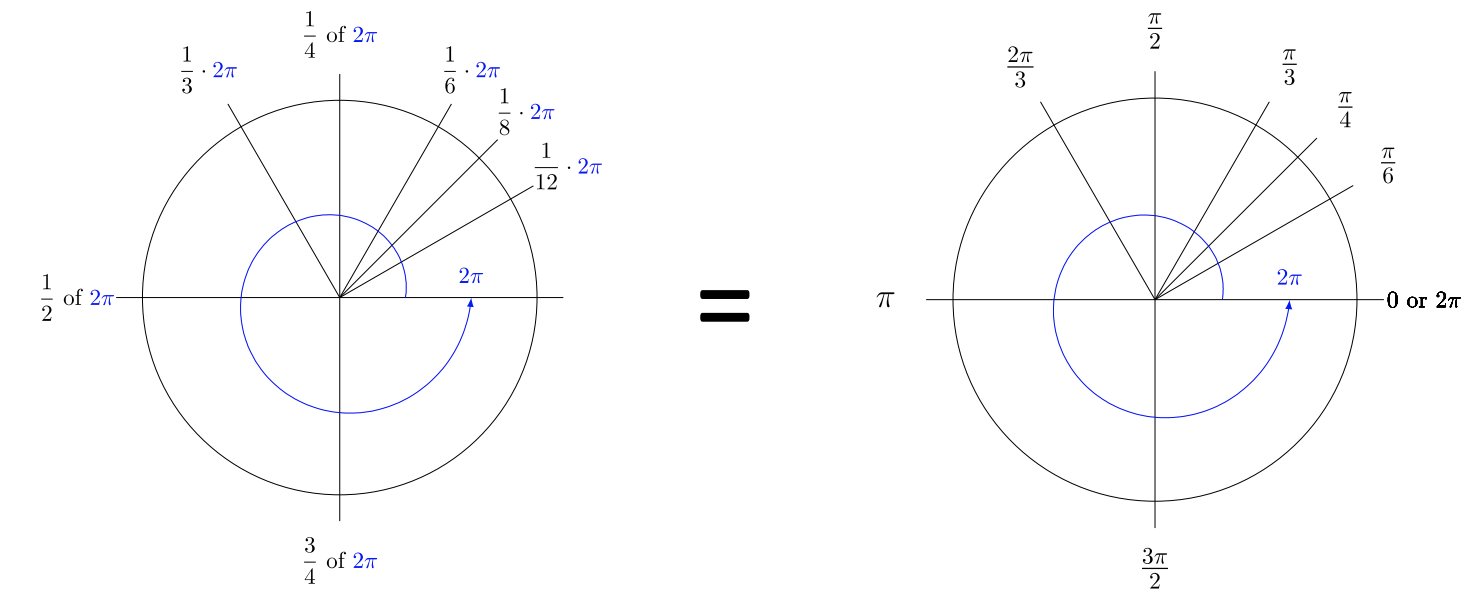
$clipboard_e96d16ca2fe5ce83c85f3fb2b53c3d2f1.png$

Як тільки ви отримаєте повісити радіани, ваші тригонометричні розрахунки швидко і легко. Використання радіанів для кутів, а не градусів, є ключем до отримання плинності в тригонометрії. Вони простіше у використанні, ніж градуси. Зверніть увагу на спільні знаменники від одного квадранта до наступного. Також зверніть увагу, що знаменник кута відповідає знаменнику власного опорного кута.

$30˚ = \dfrac{\pi}{6} \text{ radians } \;\;\;\;\;\;\;\;\;\;\;\;\; 45˚ = \dfrac{\pi}{4} \text{ radians } \;\;\;\;\;\;\;\;\;\;\;\;\; 60˚ = \dfrac{\pi}{3} \text{ radians }$

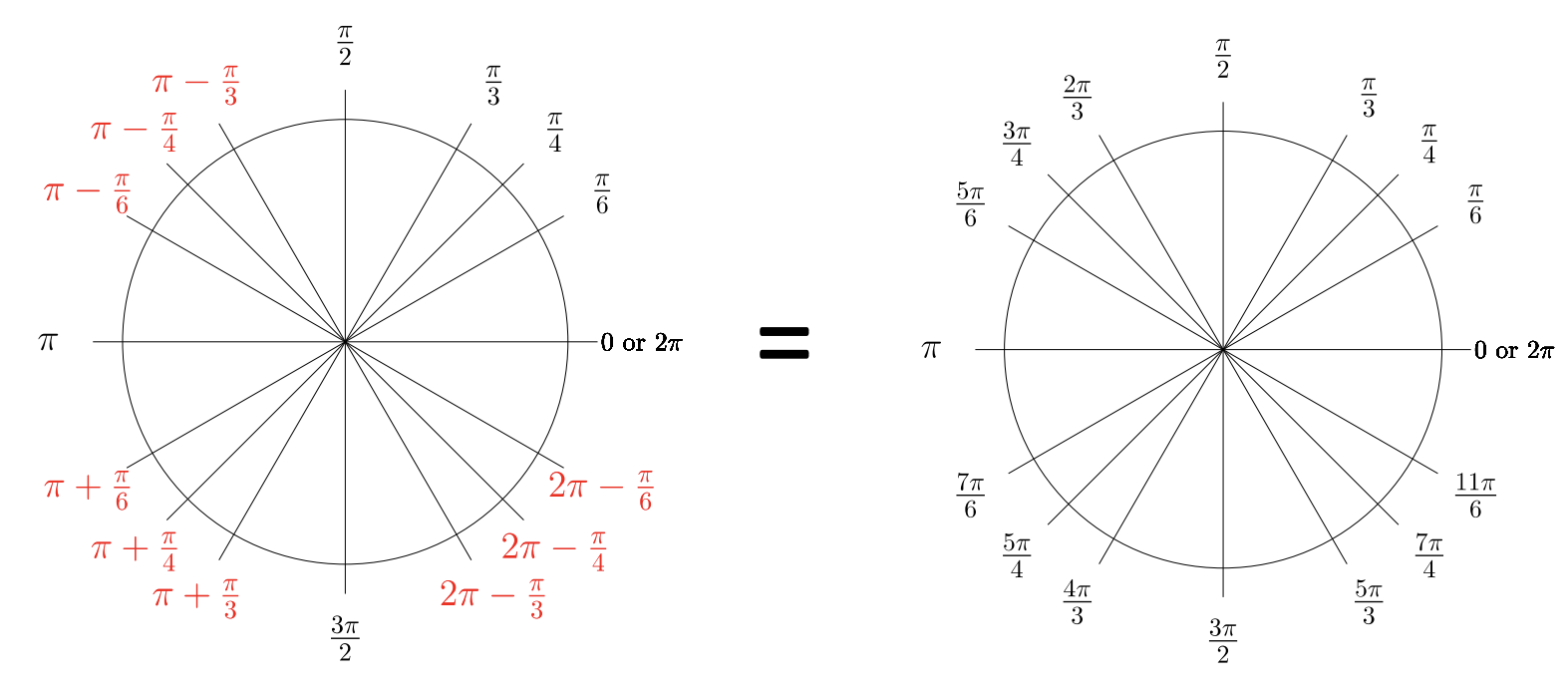
$clipboard_e457d0698b87a6baf0f73f29c9f690168.png$

Опорні кути відносяться до QI, де ваше запам'ятовування вступає в гру. Запам'ятовуйте лише QI та впорядковані пари одиничного кола в цьому квадранті (див. Розділ 7.2). Уникайте запам'ятовування занадто багато! Використовуйте інтуїтивно зрозумілі обчислення, щоб репетирувати математичні поняття. Якщо радіанове значення не є одним із зазначених вище значень, ні співтермінальним до показаних, то вам знадобиться калькулятор для тригонометричних обчислень.

Приклад Template:index

Дайте опорний кут $\hat{\theta}$ (в радіанах) для заданого стандартного кута $\theta$ . Потім накидайте обидва $\theta$ і $\hat{\theta}$ .

$\theta = \dfrac{7 \pi}{6}$
$\theta = − \dfrac{2 \pi}{3}$
$\theta = \dfrac{11 \pi}{4}$
$\theta = 6 \text{ radians}$

Рішення

$\theta = \dfrac{7 \pi}{6}$ . Вирішіть $\dfrac{7 \pi}{6}$ , чи ближче до $\pi$ чи $2 \pi$ .

Так як $\pi = \dfrac{6\pi}{6}$ і $2\pi = \dfrac{12\pi}{6}$ , зрозуміло, що $\dfrac{7\pi}{6} > \dfrac{6\pi}{6}$ і ближче до $\pi$ .

Опорний кут дорівнює $\hat{\theta} = \dfrac{\pi}{6}$ .

$\dfrac{7\pi}{6} = \pi + \dfrac{\pi}{6}$ .

Ескіз наведено нижче.

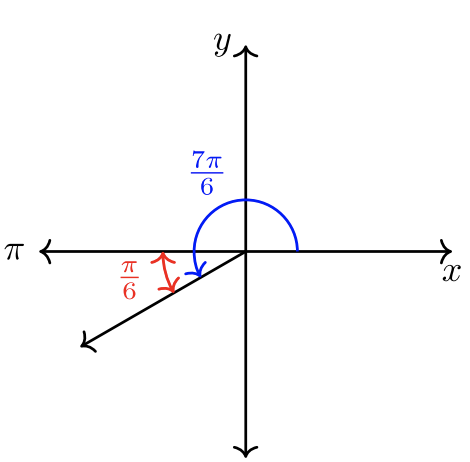
$clipboard_e758796aa951c3dfbb9b7bcb8144753ea.png$

$\theta = − \dfrac{2 \pi}{3}$ . Кут повертається за годинниковою стрілкою.

$\left|− \dfrac{2\pi}{3} \right| = \dfrac{2\pi}{3}$ який закінчується в QII.

Обертання за годинниковою стрілкою $−\dfrac{2\pi}{3}$ закінчується в QIII.

Обидва $\dfrac{2\pi}{3}$ і $−\dfrac{2\pi}{3}$ мають однаковий опорний кут.

$\hat{\theta} = \dfrac{\pi}{3}$ .

Ескіз наведено нижче.

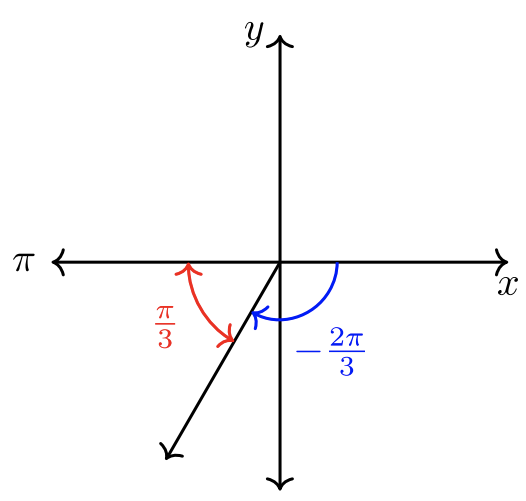
$clipboard_e2ce08b292bebde15a1d77ac730a8e8fe.png$

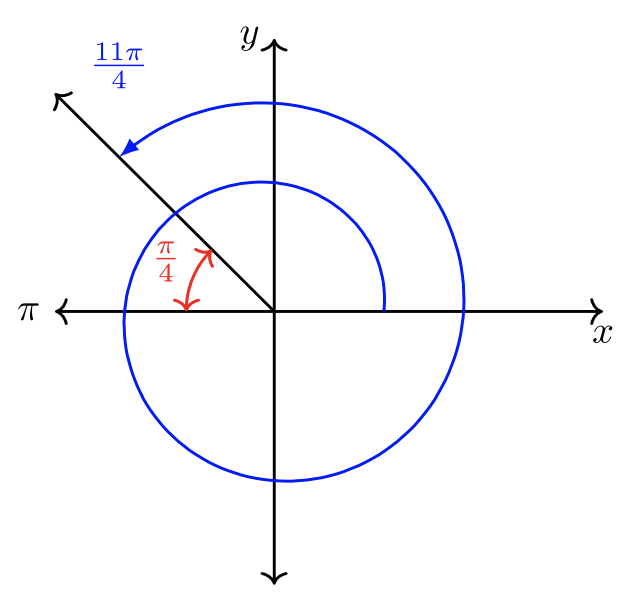
$\theta = \dfrac{11 \pi}{4}$ . Знаменником є $4$ .

Так як $\dfrac{8\pi}{4} = 2\pi$ і $\dfrac{11\pi}{4} > \dfrac{8\pi}{4}$ , цей кут обертається за один повний оборот. $\pi$ співтермінал з $3\pi$ , $5\pi$ , $7\pi$ ... в той час як $2\pi$ співтермінал з $4\pi$ , $6\pi$ , $8\pi$ ,...

$\dfrac{11\pi}{4}$ Порівняти з $3\pi = \dfrac{12\pi}{4}$ . Вони дуже близькі за вартістю! $\dfrac{11\pi}{4} < \dfrac{12\pi}{4}$ і $\dfrac{11\pi}{4}$ тому припиняється в QII. Опорний кут $\hat{\theta} = \dfrac{\pi}{4}$ .

Ескіз кута показаний нижче.

$clipboard_eed9b1562a948efe6edfab78d67e05c3b.png$

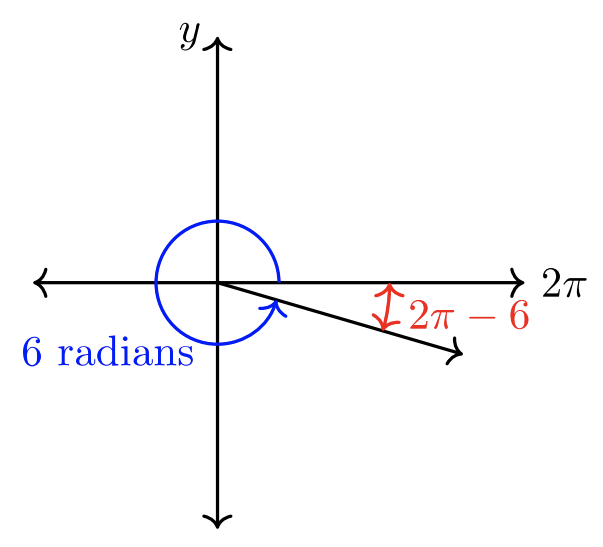
$\theta = 6 \text{ radians}$ . Вирішіть, чи є $6$ радіани ближче до $\pi$ або $2\pi$ .

Так як $\pi ≈ 3.14$ і $2\pi ≈ 6.28$ , $6$ радіани ближче до $2\pi$ . $6 < 2\pi$ , тому кут закінчується в QIV.

Опорний кут $\hat{\theta} = 2\pi − 6 ≈ 0.28$ радіани.

Ескіз кута показаний нижче.

$clipboard_ee7bece9679fcef2edbf41c496f299d1e.png$

Приклад Template:index

Кінцева сторона стандартного кута $\theta = \dfrac{3\pi}{4}$ радіанів перетинає одиничну окружність. Вкажіть впорядковану пару перехрестя.

Рішення

Так як $\dfrac{3\pi}{4} = \dfrac{4\pi}{4} − \dfrac{\pi}{4}$ кут $\theta = \dfrac{3\pi}{4}$ закінчується в QII з опорним кутом $\hat{\theta} = \dfrac{\pi}{4}$ .

Одиниця кола була введена в Розділі 7.2 для градусів-кутів. Малюнок, показаний нижче, включає радіан-кути.

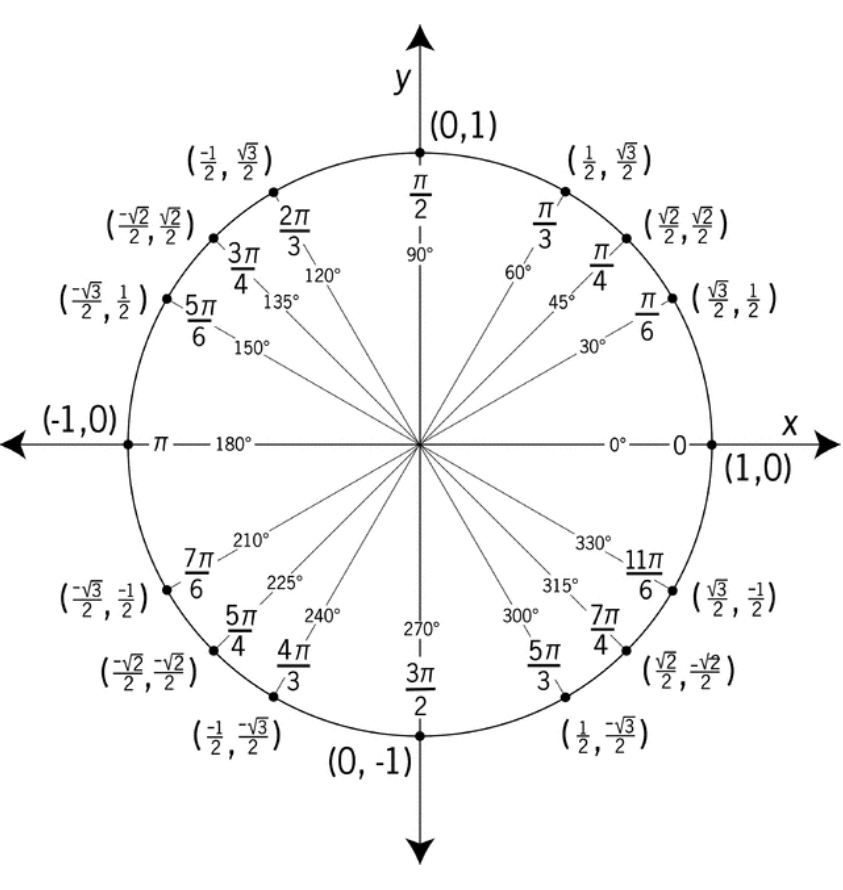
$clipboard_edf7f7bacee9db4fb14db4c139a3b04c1.png$

Впорядкована пара на одиничному колі, що перетинає кінцеву сторону $\pi = \dfrac{3\pi}{4}$ є $\left(−\dfrac{\sqrt{2}}{2} , \dfrac{\sqrt{2}}{2} \right)$ .

Приклад Template:index

Кінцева сторона стандартного кута $\theta = \dfrac{5\pi}{2}$ радіанів перетинає одиничну окружність. Вкажіть впорядковану пару перехрестя.

Рішення

Так як $\dfrac{5\pi}{2} = \dfrac{\pi}{2} + 2\pi$ , кути $\dfrac{5\pi}{2}$ і $\dfrac{\pi}{2}$ є котермінальними кутами. Котермінальні кути приземляються в одному місці, тому впорядкована пара буде однаковою. Впорядкована пара на одиничному колі, що перетинає кінцеву сторону $\theta = \dfrac{5\pi}{2}$ є $(0, 1)$ .

Приклад Template:index

Кінцева сторона стандартного кута $\theta = 10\pi$ радіанів перетинає одиничну окружність. Вкажіть впорядковану пару перехрестя.

Рішення

Так як $10\pi = 2\pi(5)$ , кути $10\pi$ і $2\pi$ є котермінальними кутами. Тому впорядкована пара на одиничному колі, що перетинає кінцеву сторону $\theta = 10\pi$ є $(1, 0)$ .

Спробуйте! (Вправи)

Для #1 -10 стандартний кут $\theta$ задається в радіанах. Вкажіть опорний кут $\hat{\theta}$ в радіанах.

$\theta = \dfrac{11\pi}{6}$
$\theta = \dfrac{7\pi}{9}$
$\theta = \dfrac{11\pi}{7}$
$\theta = 2$ радіани
$\theta = −\dfrac{5\pi}{6}$
$\theta = −\dfrac{5\pi}{4}$
$\theta = \dfrac{9\pi}{4}$
$\theta = \dfrac{17\pi}{6}$
$\theta = 10$ радіани
$\theta = −\dfrac{6\pi}{5}$

Для #11 -20 кінцева сторона заданого стандартного кута $\theta$ перетинає одиничну окружність у точці. Вкажіть впорядковану пару перехрестя.

$\theta = \dfrac{7\pi}{6}$
$\theta = \dfrac{4\pi}{3}$
$\theta = \dfrac{11\pi}{3}$
$\theta = \dfrac{7\pi}{2}$
$\theta = 5\pi$
$\theta = \dfrac{13\pi}{4}$
$\theta = −\dfrac{7\pi}{6}$
$\theta = −4\pi$
$\theta = −\dfrac{11\pi}{4}$
$\theta = −\dfrac{5\pi}{2}$

Для #21 -27 стандартний кут повороту описується словами. Вам дається кілька підказок про його обертанні. Примітка: повний оборот - $2\pi$ радіани (якщо проти годинникової стрілки) або $−2\pi$ радіани (якщо за годинниковою стрілкою). Знайдіть міру описаного кута за допомогою радіанів.

Кут має обертання проти годинникової стрілки. Кут не робить повного обороту. Кінцева сторона кута знаходиться в QIII. Опорний кут $\hat{\theta} = \dfrac{\pi}{3}$ .
Кут має обертання проти годинникової стрілки. Кут не робить повного обороту. Кінцева сторона кута знаходиться в QIV. Опорний кут $\hat{\theta} = \dfrac{\pi}{4}$ .
Кут має обертання проти годинникової стрілки. Кут не робить повного обороту. Кінцева сторона кута знаходиться в QII. Опорний кут $\hat{\theta} = \dfrac{\pi}{6}$ .
Кут має обертання за годинниковою стрілкою. Кут не робить повного обороту. Кінцева сторона кута знаходиться в QIV. Опорний кут $\hat{\theta} = \dfrac{\pi}{3}$ .
Кут має обертання за годинниковою стрілкою. Кут не робить повного обороту. Кінцева сторона кута перетинає одиничну окружність в точці $(−1, 0)$ .
Кут має обертання проти годинникової стрілки. Кут обертається більше одного повного обороту. Кінцева сторона кута перетинає одиничну окружність в точці $\left(−\dfrac{\sqrt{2}}{2}, −\dfrac{\sqrt{2}}{2} \right)$ .
Кут має обертання проти годинникової стрілки. Кут обертається більше двох повних обертів. Кінцева сторона кута перетинає одиничну окружність в точці $\left(−\dfrac{1}{2} , \dfrac{\sqrt{3}}{2} \right)$ .