7.2: Довідкові кути

Last updated
Save as PDF

Page ID: 59465

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Спеціальні прямокутні трикутники,$30˚$$60˚$ -$45˚$ -$90˚$ і$45˚$ -$90˚$, дозволяють отримати точні значення впорядкованих пар$(x, y)$ на одиничному колі зі стандартними кутами$30˚$$45˚$, або$60˚$.

Якщо ми використовуємо симетрію поперек$y$ -осі та$x$ -осі, ми можемо заповнити відомі впорядковані пари з QI в квадранти II, III та IV. Використовуйте наведені нижче цифри, щоб простежити, як це робиться. Щоб зображення були простими,$30˚$ кути$45˚$ позначені, в той час як і$60˚$ можна припустити їх більшими величинами.

Рисунок Template:index: QI → QII$(x, y) → (−x, y)$

Рисунок Template:index: QII → QIII$(−x, y) → (−x, −y)$

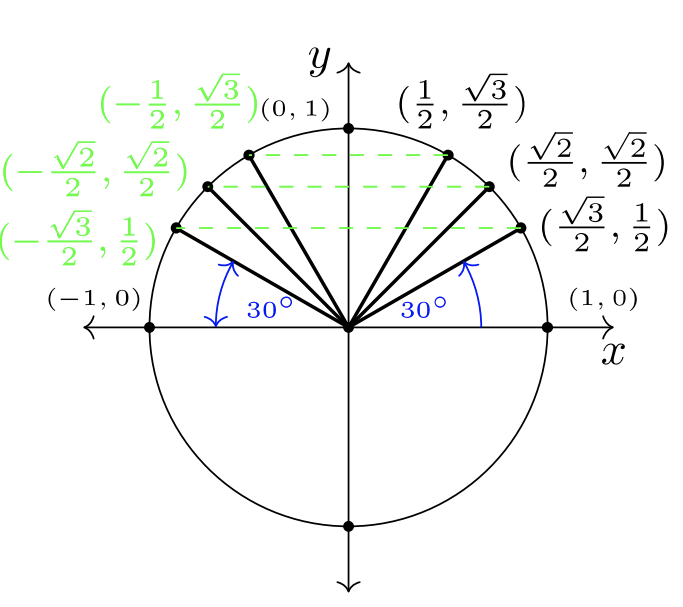
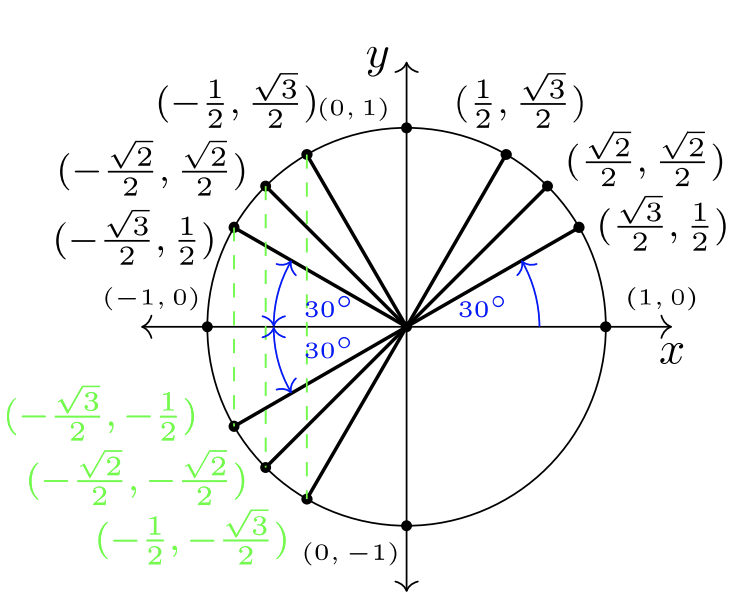
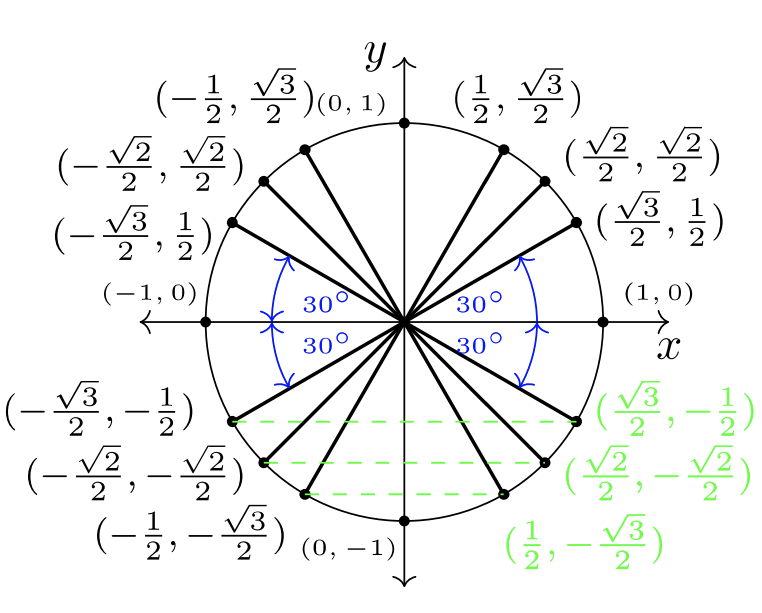
Зверніть увагу, що чотири$30˚$ кути створюють вигляд краватки-метелика на малюнку$7.2.3$. Ці кути називаються опорними кутами.

Визначення: Опорний кут

$\theta$Дозволяти бути стандартним кутом. Опорний кут, позначається$\hat{\theta}$, є позитивним гострим кутом між кінцевою стороною$\theta$ і$x$ -віссю.

Слово посилання використовується тому, що всі кути можуть посилатися на QI. Тобто запам'ятовування впорядкованих пар обмежується QI одиничного кола. Якщо стандартний кут$\theta$ має опорний кут, або$30˚$$45˚$$60˚$, впорядкована пара одиничного кола дублюється, але значення знака$x$ або$y$ може потребувати коригування, залежно від квадранта кінцевої сторони$\theta$.

Приклад Template:index

Кінцева сторона стандартного кута$\theta = 225˚$ перетинає одиничну окружність. Вкажіть впорядковану пару перехрестя.

Рішення

Одинична окружність має радіус$r = 1$. Тригонометрія з'єднує алгебру і геометрію з наочними ескізами. Починаємо з ескізу кута$\theta = 225˚$. Всі стандартні кути починаються з позитивної сторони$x$ -осі. У якому квадранті знаходиться кінцева сторона$\theta$? Тобто, де цей кут зупиняється?

Де знаходиться термінальна сторона$\theta = 225˚$? Оскільки$180˚ < 225˚ < 270˚$ кінцева сторона кута знаходиться в QIII.

Опорний кут обчислюється шляхом знаходження різниці між$225˚$ і$180˚$.

Примітка: опорний кут ніколи не є негативним.

$|225˚ − 180˚| = |180˚ − 225˚| = \hat{\theta}$

$45˚ = \hat{\theta}$

У QIII всі$(x, y)$ впорядковані пари такі, що$x < 0$ і$y < 0$. Повертаючись до QI, використовуючи стандартний кут$45˚$ на одиничному колі, впорядкована пара$\left( \dfrac{\sqrt{2}}{2} , \dfrac{\sqrt{2}}{2} \right)$ повинна бути відрегульована на негативні$x$ та$y$ координати.

Відповідь: кінцева сторона$\theta = 225˚$ перетинає одиницю окружності в$\left( −\dfrac{\sqrt{2}}{2} , −\dfrac{\sqrt{2}}{2} \right)$.

Порада: Якщо стандартний кут більше$90˚$, використовуйте маркери$180˚$ або$360˚$ для обчислення опорного кута. Малювати картинку перед обчисленням завжди рекомендується!

QII:$90˚ < \theta < 180˚$
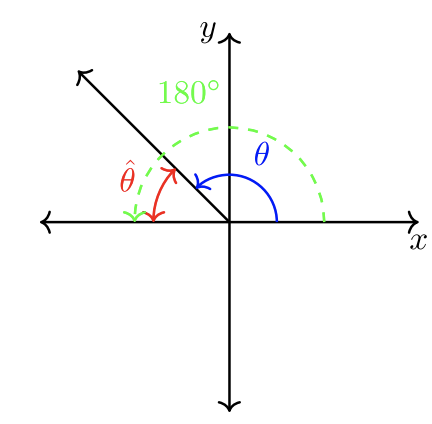
$|180˚ − \theta| = \textcolor{red}{\hat{\theta}}$

ІІІ:$180˚ < \theta < 270˚$
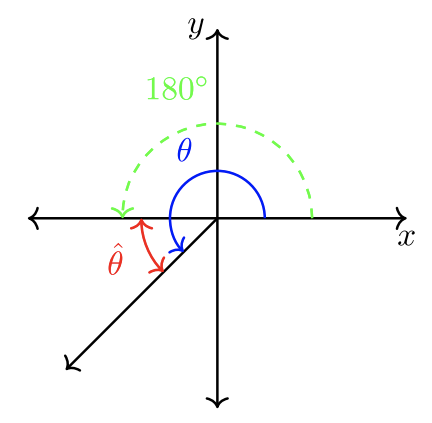
$|180˚ − \theta| = |\theta − 180˚| = \textcolor{red}{\hat{\theta}}$

QIV: Якщо$270˚ < \theta < 360˚$
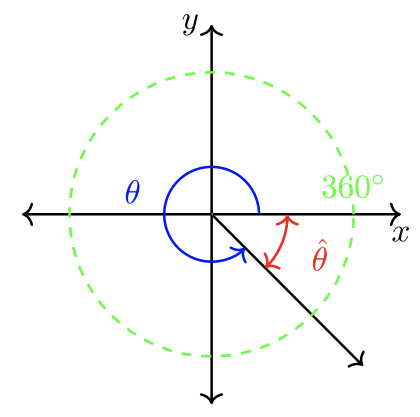
$|360˚ − \theta| = \textcolor{red}{\hat{\theta}}$

Приклад Template:index

Кінцева сторона стандартного кута$\theta = −480˚$ перетинає одиничну окружність. Вкажіть впорядковану пару перехрестя.

Рішення

Від'ємні кути повертаються за годинниковою Ескіз$\theta$. Знайдіть позитивний котермінальний кут:$−480˚ + 360˚(2) = 240˚$ Потім застосуйте наведені вище поради або проаналізуйте візуально:$|180˚ − 240˚| = |−60˚| = 60˚ = \hat{\theta}$

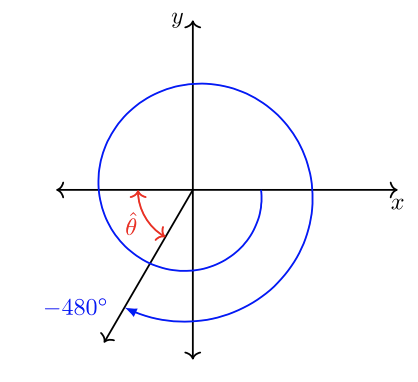
$clipboard_e2e05a1fabdfb42e49534221af0acffe0.png$

Впорядкована пара на одиничному колі дорівнює$\left(−\dfrac{1}{2} , −\dfrac{\sqrt{3}}{2} \right)$.

Спробуйте! (Вправи)

Для #1 -10 вкажіть опорний$\hat{\theta}$ кут заданого стандартного кута.

$\theta = 210˚ $
$\theta = 350˚$
$\theta = 110˚$
$\theta = 240.5˚$
$\theta = 142.75˚$
$\theta = −315˚$
$\theta = −230˚$
$\theta = 500˚$
$\theta = 615˚$
$\theta = −835˚$

Для #11 -20 кінцева сторона заданого стандартного кута$\theta$ перетинає одиничну окружність у точці. Вкажіть впорядковану пару перехрестя.

$\theta = 135˚$
$\theta = 300˚$
$\theta = −240˚$
$\theta = −150˚$
$\theta = 420˚$
$\theta = 570˚$
$\theta = 840˚$
$\theta = −765˚$
$\theta = −930˚$
$\theta = 1560˚$

Для #21 -28 поворот стандартного кута описується словами. Вам дається кілька підказок про його обертанні. Примітка: повний оборот -$360˚$ (проти годинникової стрілки) або$-360˚$ (за годинниковою стрілкою). Знайдіть міру описуваного кута.

Кут має обертання проти годинникової стрілки. Кут не робить повного обороту. Кінцева сторона кута знаходиться в QIV. Опорний кут$\hat{\theta} = 30˚$.
Кут має обертання проти годинникової стрілки. Кут не робить повного обороту. Кінцева сторона кута знаходиться в QII. Опорний кут$\hat{\theta} = 20˚$.
Кут має поворот за годинниковою стрілкою. Кут не робить повного обороту. Кінцева сторона кута знаходиться в QIII. Опорний кут$\hat{\theta} = 10˚$.
Кут має поворот за годинниковою стрілкою. Кут не робить повного обороту. Кінцева сторона кута знаходиться в QII. Опорний кут$\hat{\theta} = 72˚$.
Кут має обертання проти годинникової стрілки. Кут виходить якраз за один повний оборот. Кінцева сторона кута знаходиться в QI. Опорний кут$\hat{\theta} = 55˚$.
Кут має обертання проти годинникової стрілки. Кут виходить за рамки двох повних оборотів. Кінцева сторона кута знаходиться в QII. Опорний кут$\hat{\theta} = 24˚$.
Кут має поворот за годинниковою стрілкою. Кут виходить за рамки одного повного обороту. Кінцева сторона кута знаходиться в QIII. Опорний кут$\hat{\theta} = 18˚$.
Кут має поворот за годинниковою стрілкою. Кут виходить за рамки двох повних оборотів. Кінцева сторона кута знаходиться в QIV. Опорний кут$\hat{\theta} = 39˚$.