2.6: Розв'язування тригонометричних рівнянь

Фокус-питання

Наступні питання призначені для керівництва нашим вивченням матеріалу в цьому розділі. Вивчивши цей розділ, ми повинні зрозуміти поняття, мотивовані цими питаннями, і вміти писати точні, узгоджені відповіді на ці питання.

Для цих питань ми дозволяємо\(q\) бути дійсним числом з\(-1 \leq q \leq 1\) і нехай\(r\) бути дійсним числом.

• Як можна використовувати обернену тригонометричну функцію для визначення одного розв'язку рівняння виду\(\sin(x) = q, \cos(x) = q\), або\(\tan(x) = r\)?
• Як можна використовувати властивості тригонометричних функцій для визначення всіх розв'язків рівняння виду\(\sin(x) = q, \cos(x) = q\), або\(\tan(x) = r\)? протягом одного повного періоду тригонометричної функції?
• Як ми можемо використовувати період тригонометричної функції для визначення формули розв'язків рівняння виду\(\sin(x) = q, \cos(x) = q\), або\(\tan(x) = r\)?

Нагадаємо, що математичне рівняння,\(x^{2} = 1\) подібне до відношення між двома виразами, які можуть бути істинними для деяких значень змінної, тоді як ідентичність,\(\cos(-x) = \cos(x)\) подібне до рівняння, яке вірно для всіх допустимих значень змінної. Таким чином, ідентичність - це особливий тип рівняння. Рівняння, які не є тотожностями, також називаються умовними рівняннями, оскільки вони не є дійсними для всіх допустимих значень змінної. Вирішити рівняння означає знайти всі значення для змінних, які роблять два вирази по обидва боки рівняння рівними один одному. Ми розв'язали алгебраїчні рівняння в алгебрі і тепер будемо вирішувати тригонометричні рівняння.

Тригонометричне рівняння - це рівняння, яке включає в себе тригонометричні функції. Ми вже використовували графічні методи для наближення розв'язків тригонометричних рівнянь. У прикладі 2.17 ми використовували функцію

\[V(t) = 35\cos \left(\dfrac{5\pi}{3}t \right) + 105\]

як модель для кількості крові в серці. Для цієї функції t вимірюється в секундах, так як серце було заповнене і V .т/вимірюється в мілілітрах. Щоб визначити часи, коли в серці знаходиться 140 мілілітрів крові, нам потрібно було вирішити рівняння.

\[35\cos \left(\dfrac{5\pi}{3}t \right) + 105 = 100\]

У той час ми використовували можливість «перетину» графічної утиліти для визначення деяких розв'язків цього рівняння. У цьому розділі ми дізнаємося, як використовувати обернену функцію косинуса і властивості функції косинуса для визначення розв'язків цього рівняння. Почнемо спочатку з вивчення більш простих рівнянь.

Початок діяльності

Використовуйте утиліту графіків, щоб намалювати графіки\(y = \cos(x)\) та\(y = 0.7\) на одних і тих же осях за допомогою\(-\pi \leq x \leq \pi\) і\(-1.2 \leq y \leq 1.2\). Використовуйте утиліту графіків, щоб знайти точки перетину цих двох графіків та визначити розв'язки рівняння.\(\cos(x) = 0.7\)

На початку діяльності ми повинні були визначити наступні наближення для розв'язків рівняння\(\cos(x) = 0.7\):

• \(x_{1} \approx 0.79540\)
• \(x_{1} \approx -0.79540\)

Ці наближення округлені до п'яти знаків після коми.

На графіку нижче показані два графіки за допомогою\(-3\pi \leq x \leq 3\pi\). \(x_{2}\)Розв'язки\(x_{1}\) і наведені на графіку. Як видно, на графіку показані\(x_{1}\)\(x_{2}\) і чотири інші рішення рівняння\(\cos(x) = 0.7\). Насправді, якщо ми уявляємо графік, розширений на невизначений час вліво і вправо, ми можемо побачити, що існує нескінченно багато рішень для цього рівняння.

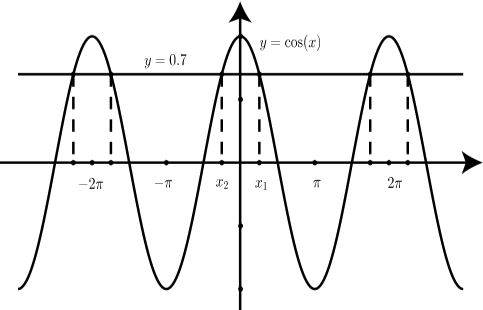
Тут ми можемо використовувати той факт, що період функції косинуса є\(2\pi\). Інші розв'язки відрізняються від\(x_{1}\) або\(x_{2}\) цілим числом, кратним періоду\(2\pi\). Ми можемо представляти ціле число, кратне\(2\pi\)\(k(2\pi)\) за деяким цілим числом\(k\). Отже, ми говоримо, що будь-яке рішення рівняння\(\cos(x) = 0.7\) може бути наближений

\[x_{1} \approx 0.79540 + k(2\pi)\]

або

\[x_{1} \approx -0.79540 + k(2\pi)\]

Наприклад, якщо ми використовуємо\(k = 4\), ми бачимо, що\(x \approx 25.92814\) або\(x \approx 24.33734\).

Ми можемо використовувати калькулятор, щоб перевірити, що для обох значень,\(\cos(x) = 0.7\).

Стратегія розв'язання тригонометричного рівняння

Приклад з використанням рівняння\(\cos(x) = 0.7\) був покликаний проілюструвати той факт, що якщо на невідоме немає обмежень\(x\), то розв'язків рівняння виду «якась тригонометрична функція\(x\)» = число може бути нескінченно багато.

Загальна стратегія вирішення таких рівнянь така:

• Знайти всі розв'язки рівняння протягом одного періоду функції. Це часто робиться за допомогою властивостей тригонометричної функції. Досить часто за один період буде два рішення.
• Використовуйте період функції для вираження формул для всіх розв'язків шляхом додавання цілих кратних періоду до кожного розв'язку, знайденого на першому кроці. Наприклад, якщо функція має період\(2\pi\) і\(x_{1}\) і\(x_{2}\) є єдиними двома розв'язками в повному періоді, то ми б запишемо розв'язки рівняння як\[x = x_{1} + k(2\pi), x = x_{2} + k(2\pi)\], де\(k\) ціле число.

Примітка

Замість того, щоб писати «\(k\)це ціле число», ми могли б написати\[k \in \{\dotsb, -2, -1, 0, 1, 2, \dotsb\}.\]

Вправа\(\PageIndex{1}\)

Використовуйте графік, щоб наблизити розв'язки (округлені до чотирьох десяткових знаків) рівняння\(\sin(x) = -0.6\) на інтервалі\(-\pi \leq x \leq \pi\). Потім використовуйте період функції синуса для написання формул, які можуть бути використані для наближення будь-якого рішення цього рівняння.

Відповідь

Будь-який розв'язок рівняння\(\sin(x) = -0.6\) може бути апроксимований одним із таких:

\[x \approx 0.64350 + k(2\pi)\]або\[x \approx 2.49809 + k(2\pi)\]

Використання обернених функцій для розв'язання тригонометричних рівнянь

Хоча ми можемо використовувати графічну утиліту для визначення наближень для розв'язків багатьох рівнянь, нам часто потрібно мати деякі позначення для позначення конкретних чисел (які часто є розв'язками рівнянь). Ми вже бачили це на попередніх курсах математики. Наприклад, ми використовуємо позначення\(\sqrt{20}\) для представлення позитивного дійсного числа, квадрат якого дорівнює\(20\). Ми можемо використовувати це, щоб сказати, що два рішення рівняння\(x^{2} = 20\)\[x = \sqrt{20} \space and \space x = -\sqrt{20}\]

Зверніть увагу, що існує два рішення рівняння, але\(\sqrt{20}\) представляє лише одне з цих розв'язків. Зараз ми дізнаємося, як використовувати обернені тригонометричні функції, щоб зробити щось подібне для тригонометричних рівнянь. Одна велика різниця полягає в тому, що більшість тригонометричних рівнянь матимуть нескінченно багато рішень замість двох. Ми будемо використовувати обернені тригонометричні функції для представлення одного рішення рівняння, а потім навчимося представляти всі розв'язки з точки зору цього рішення. Спочатку ми покажемо, як це робиться з рівнянням\(\cos(x) = 0.7\) від початку діяльності для цього розділу.

Приклад\(\PageIndex{1}\): Solving an Equation Involving the Cosine Function

Для рівняння\(\cos(x) = 0.7\) ми спочатку використовуємо результат про функцію оберненого косинуса на сторінці 150, який стверджує, що for\(t\) в замкнутому інтервалі\([0, \pi]\),\[\cos^{-1}(\cos(t)) = t\]

Отже, ми «застосуємо обернену функцію косинуса» до обох сторін рівняння\(\cos(x) = 0.7\) Це дає:

\[\cos(x) = 0.7\]

\[\cos^{-1}(\cos(x)) = \cos^{-1}(0.7)\]

\[x = \cos^{-1}(0.7) \nonumber\]

Інша річ, яку ми повинні пам'ятати, це те, що це дає одне рішення для рівняння, яке знаходиться в інтервалі\([0, \pi]\). Перш ніж використовувати властивість peredious, нам потрібно визначити інші розв'язки рівняння в одному повному періоді функції косинуса. Ми можемо використовувати інтервал,\([0, 2\pi]\) але простіше використовувати інтервал\([-\pi, \pi]\). Однією з причин цього є наступна так звана «негативна ідентичність дуги», заявлена на p вік 82.

\ [\ cos (-x) =\ cos (x)\) для кожного дійсного числа\(x\).

Отже, оскільки одне рішення для рівняння є\(x = \cos^{-1}(0.7)\), інше рішення є\(x = -\cos^{-1}(0.7)\). Це означає, що два рішення рівняння\(x = \cos(x)\) на інтервалі\([-\pi, \pi]\) є

\[x = \cos^{-1}(0.7) \space and \space x = -\cos^{-1}(0.7) \nonumber\]

Перевірити, що рівняння\(\cos(x) = 0.7\) має два рішення на інтервалі,\([-\pi, \pi]\) намалювавши графіки\(y = \cos(x)\) і\(y = 0.7\) на інтервалі\([-\pi, \pi]\). Отже, якщо ми обмежуємося цим інтервалом, у нас є щось дуже схоже на рішення рівняння\(x^{2} = 20\) в тому, що є два рішення, які є негативами один одного. Основна відмінність зараз полягає в тому, що тригонометричне рівняння має нескінченно багато розв'язків і, як і раніше, ми тепер використовуємо періодичну властивість функції косинуса. Оскільки період є\(2\pi\), так само, як і при числових наближеннях від початку діяльності, можна сказати, що будь-яке рішення рівняння\(\cos(x) = 0.7\) буде мати вигляд

\[x = \cos^{-1}(0.7) + k(2\pi) \space or \space x = -\cos^{-1}(0.7) + k(2\pi) \nonumber\]

де\(k\) є деяким цілим числом.

Вправа\(\PageIndex{2}\)

Визначте всі розв'язки рівняння\(4\cos(x) + 3 = 2\) в інтервалі\([-\pi, \pi]\). Потім використовуйте періодичну властивість функції косинуса для написання формул, які можуть бути використані для генерації всіх розв'язків цього рівняння.

Підказка

Спочатку використовуйте алгебру, щоб переписати рівняння у вигляді\(\cos(x)\) = «деяке число».

Відповідь

Спочатку перепишемо рівняння\(4\cos(x) + 3 = 2\) наступним чином:

\[\begin{align*} 4\cos(x) + 3 &= 2 \\[4pt] 4\cos(x) &= -1 \\[4pt] \cos(x) &= -\dfrac{1}{4} \end{align*}\]

Так в\([-\pi, \pi]\) інтервалі розчини є\(x_{1} = \arccos(-\dfrac{1}{4})\) і\(x_{2} = -\arccos(-\dfrac{1}{4})\). Отже, будь-яке рішення\(4\cos(x) + 3 = 2\) рівняння має вигляд

\[x = \arccos(-\dfrac{1}{4}) + k(2\pi)\]або\[x = -\arccos(-\dfrac{1}{4}) + k(2\pi) \nonumber\]

Попередні приклади показали, що при використанні функції зворотного косинуса для розв'язання рівнянь виду\(\cos(x)\) = число простіше використовувати інтервал\([-\pi, \pi]\); а не інтервал\([0, 2\pi]\). Це не обов'язково вірно при використанні функції зворотного синуса, оскільки функція зворотного синуса дає значення в інтервалі\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\). Однак, щоб зберегти речі подібними, ми продовжуватимемо використовувати інтервал\([-\pi, \pi]\); як повний період для функції синуса (або косинуса). Для зворотного синуса ми використовуємо наступну властивість, зазначену на сторінці 147.

Для кожного t в замкнутому\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\) інтервалі\[\sin^{-1}(sin(t)) = t\]

При розв'язанні рівнянь, що включають функцію косинуса, ми також використовували від'ємну дугову ідентичність. Ми робимо те ж саме і будемо використовувати наступну негативну дугу ідентичність, зазначену на сторінці 82. \[\sin(-x) = -\sin(x)\]для кожного дійсного числа\(x\).

Приклад\(\PageIndex{2}\): Solving an Equation Involving the Sine Function

Ми проілюструємо загальний процес, використовуючи рівняння\(\sin(x) = -0.6\) з Progress Check 2.34. Через негативну ідентичність дуги для синусоїдальної функції насправді простіше працювати з рівнянням\(\sin(x) = 0.6\). Це тому, що якщо\(x = a\) це рішення рівняння\(\sin(x) = 0.6\), то\[\sin(-a) = -\sin(a) = -0.6\]

і так,\(x = -a\) є розв'язком рівняння\(\sin(x) = -0.6\). Для\(\sin(x) = 0.6\) рівняння ми починаємо з «застосування функції зворотного синуса» до обох сторін рівняння.

\[\sin(x) = 0.6\]\[\sin^{-1}(\sin(x)) = \sin^{-1}(0.6)\]\[x = \sin^{-1}(0.6)\]

Потрібно пам'ятати, що це тільки одне рішення рівняння. Оскільки ми знаємо, що функція синуса позитивна в першому та другому квадрантах, це рішення знаходиться в першому квадранті і є інше рішення у другому квадранті. Використовуючи\(x = \sin^{-1}(0.6)\) як опорну дугу (кут), рішення у другому квадранті є\(x = \pi - \sin^{-1}(0.6)\). Тепер ми використовуємо результат, що якщо\(x = a\) це рішення рівняння\(\sin(x) = 0.6\), то\(x = -a\) є рішенням рівняння\(\sin(x) = -0.6\). Будь ласка, зверніть увагу, що\[-(\pi - \sin^{-1}(0.6)) = -\pi + \sin^{-1}(0.6)\]

Наша робота поки зведена в наступну таблицю.

Рішення для\(\sin(x) = 0.6\) в\([0, \pi]\)	Рішення для\(\sin(x) = -0.6\) в\([-\pi, 0]\)
\(x = \sin^{-1}(0.6)\)	\(x = -\sin^{-1}(0.6)\)
\(x = \pi - \sin^{-1}(0.6)\)	\(x = -\pi + \sin^{-1}(0.6)\)

На цьому етапі ми повинні використовувати калькулятор, щоб переконатися, що два значення в правій колонці насправді є розв'язками рівняння\(\sin(x) = -0.6\). Тепер, коли ми маємо рішення для\(\sin(x) = -0.6\) одного повного циклу, ми можемо використовувати той факт, що період синусоїдальної функції є\(2\pi\) і сказати, що розв'язки рівняння\(\sin(x) = -0.6\) мають вигляд

\[x = -\sin^{-1}(0.6) + k(2\pi) \space or \space x = (-\pi + \sin^{-1}(0.6)) + k(2\pi) \nonumber\]

де\(k\) є деяким цілим числом.

Вправа\(\PageIndex{3}\)

Визначте всі розв'язки рівняння\(2\sin(x) + 1.2 = 2.5\) в інтервалі\([-\pi, \pi]\) Потім використовуйте періодичну властивість синусоїдальної функції для написання формул, які можуть бути використані для генерації всіх розв'язків цього рівняння.

Підказка: Спочатку використовуйте алгебру, щоб переписати рівняння у вигляді\(sin(x)\) = «деяке число».

Відповідь

Спочатку використовуємо алгебру, щоб переписати рівняння\(2\sin(x) + 1.2 = 2.5\) у вигляді

\[\sin(x) = 0.65\]

Так в\([-\pi, \pi]\) інтервалі розчини є\(x_{1} = \arcsin(0.65)\) і\(x_{2} = \pi - \arcsin(0.65)\). Отже, будь-яке рішення\(2\sin(x) + 1.2 = 2.5\) рівняння має вигляд

\[x = \arcsin(0.65) + k(2\pi)\]або\[x = \pi - \arcsin(0.65) + k(2\pi)\]

Розв'язування більш складних тригонометричних рівнянь

Ми тепер навчилися вирішувати рівняння виду\(\cos(x) = q\), і\(\sin(x) = q\), де\(q\) знаходиться дійсне число і\(-1 \leq q \leq 1\). Ми можемо використовувати нашу здатність вирішувати ці типи рівнянь, щоб допомогти вирішити більш складні рівняння виду\(\cos(f(x)) = q\), і\(\sin(f(x)) = q\) де\(f\) є якась функція. Ідея (що характерно в математиці) полягає в тому, щоб перетворити цю більш складну задачу на дві простіші завдання. Ідея полягає в тому, щоб:

1. Зробіть підстановку,\(t = f(x)\) щоб отримати рівняння виду\(\cos(t) = q\), або\(\sin(t) = q\).
2. Розв'яжіть рівняння в (1) for\(t\).
3. Для кожного\(t\) розв'язку рівняння в (1) розв'яжіть рівняння\(f(x) = t\) для\(x\). Цей крок може бути легким, складним або, можливо, неможливим залежно від рівняння\(f(x) = t\).

Цей процес буде проілюстрований у наступній перевірці прогресу, яка буде керованим дослідженням для вирішення рівняння\(3\cos(2x + 1) + 6 = 5\).

Вправа\(\PageIndex{4}\)

Ми будемо вирішувати рівняння\(3\cos(2x + 1) + 6 = 5\).

1. Спочатку використовуйте алгебру, щоб переписати рівняння у вигляді\(\cos(2x + 1) = -\dfrac{1}{3}\). Потім зробіть заміну\(t = 2x + 1\).
2. Визначте всі розв'язки рівняння\(\cos(t) = -\dfrac{1}{3}\) с\(-\pi \leq t \leq \pi\).
3. Для кожного з цих двох рішень використовуйте\(t = 2x + 1\) для пошуку відповідних рішень для\(x\). Крім того, використовуйте підстановку,\(t = 2x + 1\) щоб написати\(-\pi \leq 2x + 1 \leq \pi\) і вирішити цю нерівність для\(x\). Це дасть всі розв'язки рівняння\(\cos(2x + 1) = -\dfrac{1}{3}\) в одному повному циклі функції, заданої\(y = \cos(2x + 1)\)
4. Що таке період функції\(y = \cos(2x + 1)\). Використовуйте результати в (3) і цей період, щоб написати формули, які будуть генерувати всі розв'язки рівняння\(\cos(2x + 1) = -\dfrac{1}{3}\). Це будуть розв'язки вихідного рівняння\(3\cos(2x + 1) + 6 = 5\).

Відповідь

1. \[3\cos(2x + 1) + 6 = 5\]\[3\cos(2x + 1) = -1\]\[\cos(2x + 1) = -\dfrac{1}{3}\]

2. \(t = \cos^{-1}(-\dfrac{1}{3})\)або\(t = -\cos^{-1}(-\dfrac{1}{3})\).

3. \[2x + 1 = \cos^{-1}(-\dfrac{1}{3})\]

\[2x = \cos^{-1}(-\dfrac{1}{3}) - 1\]

\[x = \dfrac{1}{2}\cos^{-1}(-\dfrac{1}{3}) - \dfrac{1}{2}\]

\[2x + 1 = -\cos^{-1}(-\dfrac{1}{3})\]

\[2x = -\cos^{-1}(-\dfrac{1}{3}) - 1\]

\[x = -\dfrac{1}{2}\cos^{-1}(-\dfrac{1}{3}) - \dfrac{1}{2}\]

4. Період виконання функції\(y = \cos(2x + 1)\). Таким чином, наступні формули можуть бути використані для генерації розв'язків рівняння.

\[x = (\dfrac{1}{2}\cos^{-1}(-\dfrac{1}{3}) - \dfrac{1}{2}) + k\pi\]або\[x = (-\dfrac{1}{2}\cos^{-1}(-\dfrac{1}{3}) - \dfrac{1}{2}) + k\pi\]

де\(k\) є деяким цілим числом. Зверніть увагу, що ми додали ціле число, кратне періоду, який є\(\pi\), до розв'язків в (3).

Розв'язування рівнянь за участю тангенсної функції

Рішення рівняння виду\(\tan(x) = q\) дуже схоже на рішення рівнянь виду\(\cos(x) = q\) або\(\sin(x) = q\). Основні відмінності полягають в тому, що тангенс функція має період\(\pi\) (замість\(2\pi\)), а рівняння\(\tan(x) = q\) має тільки одне рішення в повному періоді. Ми, звичайно, використовуємо обернену функцію тангенса для рівняння\(\tan(x) = q\).

Вправа\(\PageIndex{5}\)

Використовуйте обернену функцію дотичної для визначення одного розв'язку рівняння\[4\tan(x) + 1 = 10\] в інтервалі\((-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2})\). Потім визначте формулу, яка може бути використана для генерації всіх розв'язків цього рівняння.

Відповідь

Спочатку запишемо рівняння\(4\tan(x) + 1 = 10\) у вигляді\(\tan(x) = \dfrac{9}{4}\). Таким чином, єдиним рішенням рівняння в інтервалі\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\) є

\[x = \arctan(\dfrac{9}{4})\]

Так як період дотичної функції є\(\pi\), будь-який розв'язок цього рівняння може бути записаний у вигляді,\[x = \arctan(\dfrac{9}{4}) + k\pi\] де\(k\) є деяким цілим числом.

Резюме

Тригонометричне рівняння - це рівняння, яке включає в себе тригонометричні функції. Якщо ми можемо записати тригонометричне рівняння у вигляді «якась тригонометрична функція\(x\)» = число, то ми можемо використовувати наступну стратегію для вирішення рівняння.

• Знайдіть один розв'язок рівняння, використовуючи відповідну обернену тригонометричну функцію.
• Визначте всі розв'язки рівняння протягом одного повного періоду тригонометричної функції. (Це часто передбачає використання опорної дуги на основі розчину, отриманого на першому кроці.)
• Використовуйте період функції для написання формул для всіх розв'язків тригонометричного рівняння.