2.5: Зворотні тригнометричні функції

Last updated
Save as PDF

Page ID: 59324

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Фокус-питання

Наступні питання призначені для керівництва нашим вивченням матеріалу в цьому розділі. Вивчивши цей розділ, ми повинні зрозуміти поняття, мотивовані цими питаннями, і вміти писати точні, узгоджені відповіді на ці питання.

Чому функція синуса насправді не має зворотного? Що ми маємо на увазі, тоді, під зворотною функцією синуса? Іншими словами, як визначається функція зворотного синуса?
Як визначається функція зворотного косинуса?
Як визначається функція оберненої дотичної?

Початок діяльності

Якщо$y = 5x + 7$ і$y = 4$, яка цінність$x$?
Якщо$y = \sqrt{x}$ і$y = 2.5$, яка цінність$x$?
Якщо$y = x^{2}$ і$y = 25$, які можливі значення$x$?
Якщо$y = \sin(x)$ і$y = 1$, знайдіть два значення для$x$ з$0 \leq x \leq 2.2$

Вступ

Робота на початку діяльності ілюструє загальну проблему, що якщо нам дають функцію$f$ і$y = f(x)$, чи можемо ми знайти значення,$x$ якщо ми знаємо значення$y$. По суті, це означає, що якщо ми знаємо значення$y$, ми можемо вирішити для значення$x$? Для першої проблеми ми можемо замінити$y = 4$$y = 5x + 7$ і вирішити для$x$. Це дає\[4 = 5x + 7\]\[-3 = 5x\]\[x = \dfrac{-3}{5}\]
Для другої та третьої задач ми маємо\[2.5 = \sqrt{x}\]\[2.5^{2} = (\sqrt{x})^{2}\]\[x = 6.25\]\[25 = \sqrt{x}\]\[x = \pm(\sqrt{25})\]\[x = \pm5\]
Робота з рівнянням$x^{2} = 25$ показує, що ми можемо мати більше одного розв'язку для цього типу задач . За допомогою тригонометричних функцій ми можемо навіть мати більше рішень. Наприклад, якщо$y = \sin(x)$ і$y = \dfrac{1}{2}$, у нас є\[\sin(x) = \dfrac{1}{2}\]

Якщо обмежити значення$0 \leq x \leq 2\pi$, то буде два рішення, як показано на малюнку 2.32

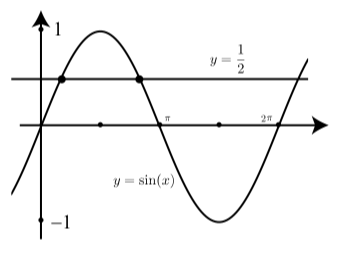
$2.32 пнг$

Малюнок$\PageIndex{1}$: Графік показу$\sin(x) = \dfrac{1}{2}$

З наших знань про загальні дуги та опорні дуги, ці два рішення є$x = \dfrac{\pi}{6}$ і$x = \dfrac{5\pi}{6}$. Крім того, періодичний характер синусоїдальної функції говорить нам про те, що якщо немає обмежень на$x$, розв'язків рівняння буде нескінченно багато$\sin(x) = \dfrac{1}{2}$. Те, що ми хочемо розробити, - це метод, щоб вказати саме одне з цих рішень. Але який з них ми виберемо?

Ми зробили щось подібне, коли вирішуємо таке рівняння, як$x^{2} = 25$. Існує два рішення цього рівняння, але у нас є функція (функція квадратного кореня), яка дає нам рівно одну з цих двох функцій. Таким чином, коли ми пишемо$x = \sqrt{25} = 5$, ми вказуємо тільки позитивне рішення рівняння. Якщо ми хочемо іншого рішення, ми повинні написати$x = -\sqrt{25} = -5$. Зверніть увагу, що ми використовували функцію квадратного кореня для позначення «простішого» двох функцій, а саме позитивного рішення.

Для функції синуса, що ми хочемо, це функція зворотного синуса, яка робить саме те, що випливає з назви - однозначно змінює те, що робить функція синуса. Тобто функція зворотного синуса приймає значення з діапазону синусоїдальної функції і дає нам рівно одну дугу, синус якої має це значення. Ми постараємося зробити це максимально простим способом. (Іноді важко повірити, але математики, як правило, намагаються робити речі простими.) Щоб бути більш конкретним, якщо у нас є$y = \sin(x)$, ми хочемо мати можливість вказати будь-яке значення для$y$ з$-1 \leq y \leq 1$ і отримати одне значення для$x$. Ми виберемо значення для$x$ того, щоб якомога ближче до 0. (Тримайте це просто.)

Тому переконайтеся, що існує тільки одне рішення, обмежимося графіком$y = \sin(x)$ інтервалу$-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$. Це також гарантує, що,$-1 \leq y \leq 1$ як показано на малюнку 2.33.

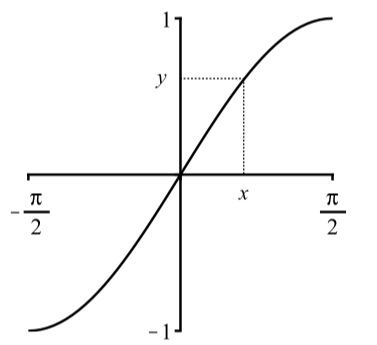
$2.33.png$

Малюнок$\PageIndex{2}$: Графік$y = \sin(x)$ обмеженого$-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$

Як показано на малюнку$\PageIndex{2}$, для кожного значення$y$ з$-1 \leq y \leq 1$ існує рівно одне значення$x$ з$\sin(x) = y$ і$-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$.

Визначення

Функція зворотного синуса (позначається$\arcsin$ або$sin^{-1}$), визначається наступним чином:
For$-1 \leq y \leq 1$,\[t = \arcsin(y) \space or \space t = sin^{-1}(y)\] означає\[y = \sin(t) \space and \space -\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}.\] $сторінка 161 зображення 21512256$ $сторінка 161 зображення 21512544$

Обережність. Для функції arcsine може бути використано будь-яке позначення. Тобто,$\arcsin(y)$ і$sin^{-1}(y)$) означають одне і те ж. Однак позначення$sin^{-1}$) означає не зворотний синус, а навпаки, зворотний синус з обмеженим доменом. Дуже важливо пам'ятати факти, що область зворотного синуса - це інтервал,$[-1, 1]$ а діапазон зворотного синуса - інтервал.$[-\dfrac{\pi}{2}, \dfrac{\pi}{2}].$

Примітка

Деякі люди вважають за краще використовувати$t = \arcsin(y)$ замість$t = sin^{-1}(y)$), оскільки це може бути нагадуванням про те, що означає позначення. Рівняння$t = \arcsin(y)$ є абревіатурою для$t$ дуги зі значенням синуса$y$ і$-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$.

Важливо продовжувати писати обмеження,$-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$ оскільки важливо розуміти, що$\arcsin(y)$ функція дає лише одну дугу, значення синуса якої є$y$ і$t$ має бути в цьому інтервалі.

Приклад$\PageIndex{1}$: Inverse Sine Function

Визначимо точне значення$\arcsin(\dfrac{\sqrt{3}}{2})$. Так ми дозволимо$t = \arcsin(\dfrac{\sqrt{3}}{2})$

Це означає, що\[\sin(t) = \dfrac{\sqrt{3}}{2}\] і\[-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}.\]

Тобто ми намагаємося знайти дугу t, синус якої дорівнює$\dfrac{\sqrt{3}}{2}$ і$-\dfrac{\pi}{2} \leq y \leq \dfrac{\pi}{2}$. Використовуючи наші знання значень синусів для загальних дуг, ми помічаємо, що$\sin(\dfrac{\pi}{3}) = \dfrac{\sqrt{3}}{2}$ і так робимо висновок про те$t = \dfrac{\pi}{3}$ чи інше\[\arcsin(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\]

Це проілюстровано графічно на малюнку$\PageIndex{3}$.

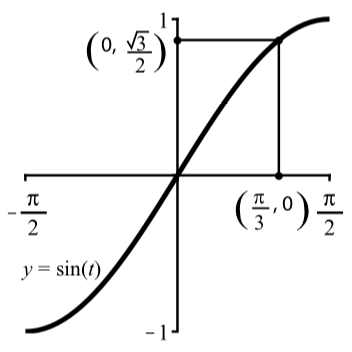
$2.34 пнг$

Малюнок$\PageIndex{3}$: Графічна версія$\arcsin(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}$

Примітка: Більшість калькуляторів і графічних утиліт можуть обчислити приблизні значення для функції зворотного синуса. На калькуляторах він часто є$\sin^{-1}$ ключовим і для багатьох комп'ютерних програм необхідно набирати «arcsin». Використовуючи калькулятор, ми бачимо$\arcsin(\dfrac{\sqrt{3}}{2}) \approx 1.04720$, що, який є десятковим наближенням для$\dfrac{\pi}{3}$.

Вправа$\PageIndex{1}$

$\arcsin(-\dfrac{\sqrt{3}}{2})$
$\sin^{-1}(\dfrac{1}{2})$
$\arcsin(-1)$
$\arcsin(-\dfrac{\sqrt{2}}{2})$

У наступній перевірці прогресу ми будемо використовувати функцію зворотного синуса в двоетапних розрахунках. Будь ласка, зверніть увагу на отримані результати.

Відповідь

1. $\arcsin(-\dfrac{\sqrt{3}}{2}) = -\dfrac{\pi}{3}$так як$\sin(-\dfrac{\pi}{3}) = -\dfrac{\sqrt{3}}{2}$ і$-\dfrac{\pi}{2} \leq -\dfrac{\pi}{3} \leq \dfrac{\pi}{2}$.

2. $\sin^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{6}$так як$\sin(\dfrac{\pi}{2}) = -\dfrac{1}{2}$ і$-\dfrac{\pi}{2} \leq \dfrac{\pi}{6} \leq \dfrac{\pi}{2}$.

3. $\arcsin(-1) = -\dfrac{\pi}{2}$так як$\sin(-\dfrac{\pi}{2}) = -1$ і$-\dfrac{\pi}{2} \leq -\dfrac{\pi}{2} \leq \dfrac{\pi}{2}$.

4. $\arcsin(-\dfrac{\sqrt{2}}{2}) = -\dfrac{\pi}{4}$так як$\sin(-\dfrac{\pi}{4}) = -\dfrac{\sqrt{2}}{2}$ і$-\dfrac{\pi}{2} \leq -\dfrac{\pi}{4} \leq \dfrac{\pi}{2}$.

Вправа$\PageIndex{2}$

Визначте точне значення кожного з наступних. Ви можете перевірити свої результати за допомогою калькулятора.

$\sin(\sin^{-1}(\dfrac{1}{2}))$
$\arcsin(\sin(\dfrac{\pi}{4}))$
$\sin(\sin^{-1}(\dfrac{1}{2}))$
$\arcsin(\sin(\dfrac{3\pi}{4}))$

Відповідь

1. З тих пір$\sin^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{6}$, ми бачимо, що$\sin(\sin^{-1}(\dfrac{1}{2})) = \sin(\dfrac{\pi}{6}) = \dfrac{1}{2}$

2. $\arcsin(\sin(\dfrac{\pi}{4})) = \arcsin(\dfrac{\sqrt{2}}{2})$. Крім того,$\arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}$ так як$\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}$ і$-\dfrac{\pi}{2} \leq -\dfrac{\pi}{4} \leq \dfrac{\pi}{2}$. Таким чином, ми бачимо, що\[\arcsin(\sin(\dfrac{\pi}{4})) = \arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}.\]

3. Ми не знаємо точного значення для$\sin^{-1}(\dfrac{2}{5})$. Так ми дозволимо$t = \sin^{-1}(\dfrac{2}{5})$.

Тоді ми знаємо, що$\sin(t) = \dfrac{2}{5}$$-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}$ і.Так

\[\sin(\sin^{-1}(\dfrac{2}{5})) = \sin(t) = \dfrac{2}{5}\]

4. $\arcsin(\sin(\dfrac{\pi}{4})) = \arcsin(\dfrac{\sqrt{2}}{2})$. Крім того,$\arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}$ так як$\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}$ і$-\dfrac{\pi}{2} \leq \dfrac{\pi}{4} \leq \dfrac{\pi}{2}$. Таким чином, ми бачимо, що\[\arcsin(\sin(\dfrac{\pi}{4})) = \arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\]

Робота у Вправі$\PageIndex{2}$ ілюструє деякі важливі властивості зворотної функції, коли вона складається з синусоїдної функції. Ця властивість полягає в тому, що в деякому сенсі зворотний синус і синус функції «скасовують» один одного. Щоб подивитися, що це означає, дозволимо$y = \sin(t)$ с$-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}$. Потім\[\sin^{-1}(\sin(t)) = \sin^{-1}(y) = t\] за визначенням. Це означає, що якщо ми застосуємо синус, то зворотний синус до дуги між$-\dfrac{\pi}{2}$ і$\dfrac{\pi}{2}$, ми отримаємо назад дугу. Це те, що ми маємо на увазі, коли ми говоримо зворотний синус скасовує синус.
Аналогічно, якщо$t = \sin^{-1}(y)$ для деяких$y$ з$-1 \leq y \leq 1$, то\[\sin(\sin^{-1}(y)) = \sin(t) = y\] за визначенням. Таким чином, синус також скасовує зворотний синус. Ми підсумовуємо ці два результати наступним чином:

Властивості функції зворотного синуса

Для кожного t в замкнутому інтервалі$[-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$,\[\sin^{-1}(\sin(t)) = t.\]
Для кожного y в замкнутому інтервалі$[-1, 1]$,\[\sin(\sin^{-1}(y)) = y.\]

Функції обернених косинусів та обернених тангенсів

Подібно до того, як ми визначили функцію зворотного синуса, ми можемо визначити обернений косинус і обернений тангенс функції. Ключ полягає в тому, щоб обмежити область відповідної кругової функції так, щоб ми отримали графік функції один до одного. Таким чином, ми будемо використовувати$y = \cos(t)$ з$0 \leq t \leq \pi$ і$y = \tan(t)$ з$-\dfrac{\pi}{2} < t < \dfrac{\pi}{2}$, як показано на малюнку$\PageIndex{4}$.

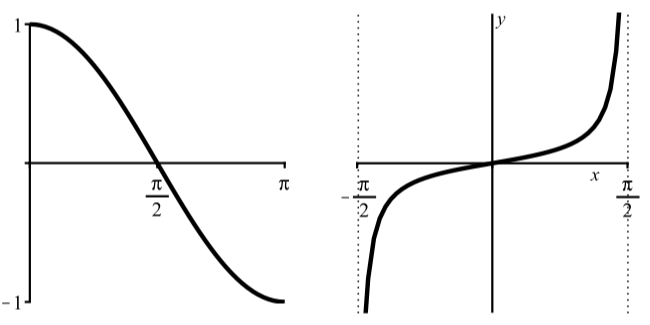
$2.35 пнг$

Малюнок$\PageIndex{4}$: Графік$y = \cos(t)$ для$0 \leq t \leq \pi$ та Графік$y = \tan(t)$ для$-\dfrac{\pi}{2} < t < \dfrac{\pi}{2}$.

Примітка

Ми не використовуємо інтервал$-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}$ для функції косинуса, оскільки функція косинуса не є один до одного на цьому інтервалі. Крім того, інтервал для функції дотичної не містить кінцевих точок, оскільки функція дотичної не визначена в і$-\dfrac{\pi}{2}$ і$\dfrac{\pi}{2}$.

Використовуючи ці області, ми тепер визначаємо зворотні функції для косинуса і тангенса.

Визначення

Функція зворотного косинуса (позначається$\arccos$ або$cos^{-1}$), визначається наступним чином:
For$-1 \leq y \leq 1$,\[t = \arccos(y) \space or \space t = cos^{-1}(y)\] щоб означати\[y = \cos(t) \space and \space 0 \leq x \leq \pi.\] $сторінка 161 зображення 21512256$ $сторінка 161 зображення 21512544$

Визначимо обернену дотичну функцію (позначається$\arctan$ або$tan^{-1}$) наступним чином:
For$t \in \mathbb{R}$,\[t = \arctan(y) \space or \space t = tan^{-1}(y)\] означає\[y = \tan(t) \space and \space -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}.\] $сторінка 161 зображення 21512256$ $сторінка 161 зображення 21512544$

Примітка

Попередні результати можуть бути записані за допомогою функції arcsine, а не$\sin^{-1}$. Дуже важливо усвідомити, що ці результати дійсні лише для\ (-\ dfrac {\ pi} {2}\ leq x leq\ dfrac {\ pi} {2}\] і\[-1 \leq y \leq 1.\]

Приклад$\PageIndex{2}$: An Example of Inverse Cosine

Рівняння$y = \arccos(-\dfrac{1}{2}) = \cos^{-1}(-\dfrac{1}{2})$ означає, що$\cos(y) = -\dfrac{1}{2}$ і$0 \leq y \leq \pi$.

Тобто ми намагаємося знайти дугу, косинус$y$ якої є$0 \leq y \leq \pi$. Використовуючи наші знання значень косинусів для загальних дуг, ми помічаємо, що$\cos(\dfrac{\pi}{3}) = \dfrac{1}{2}.$ Таким чином, ми робимо висновок, що опорний кут$\hat{y}$ для$y$ є$\hat{y} = \dfrac{\pi}{3}$. Оскільки$y$ повинен бути в QII, робимо висновок, що$y = \pi - \dfrac{\pi}{3}$ або$y = \dfrac{2\pi}{3}$. Так\[\arccos(-\dfrac{1}{2}) = \dfrac{2\pi}{3}.\]

Це можна перевірити за допомогою калькулятора і проілюстровано на малюнку$\PageIndex{5}$.

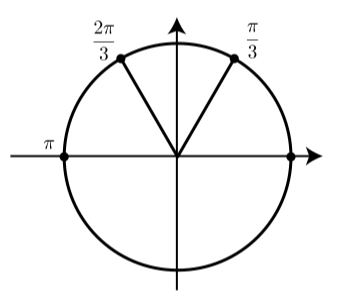
$2.36.png$

Малюнок$\PageIndex{5}$: Діаграма, що використовується для оберненого косинуса$-\dfrac{1}{2}$.

Вправа$\PageIndex{3}$

$\cos(\cos^{-1}(\dfrac{1}{2}))$
$\arccos(\cos(\dfrac{\pi}{4}))$
$\arccos(\cos(\dfrac{-\pi}{4}))$
$\tan^{-1}(\tan(\dfrac{5\pi}{4}))$

Робота у Вправі$\PageIndex{2}$ ілюструє деякі важливі властивості оберненої косинусної та оберненої дотичної функцій, аналогічних властивостям функції зворотного синуса на сторінці 147.

Відповідь

1. З тих пір$\cos^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{3}$, ми це бачимо$\cos(\cos^{-1}(\dfrac{1}{2})) = \cos(\dfrac{\pi}{3}) = \dfrac{1}{2}$.

2. $\arccos(\cos(\dfrac{\pi}{4})) = \arccos(\dfrac{\sqrt{2}}{2})$. Крім того,$\arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}$ так як$\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}$ і$0 \leq \dfrac{\pi}{4} \leq \pi$. Таким чином, ми бачимо, що\[\arccos(\cos(\dfrac{\pi}{4})) = \arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}.\]

3. $\arccos(\cos(-\dfrac{\pi}{4})) = \arccos(\dfrac{\sqrt{2}}{2})$. Крім того,$\arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}$ так як$\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}$ і$0 \leq \dfrac{3\pi}{4} \leq \pi$. Таким чином, ми бачимо, що\[\arccos(\cos(-\dfrac{\pi}{4})) = \arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}.\]

4. $\tan^{-1}(\tan(\dfrac{5\pi}{4})) = \tan^{-1}(1)$. Крім того,$\tan^{-1}(1) = \dfrac{\pi}{4}$ так як$\tan(\dfrac{\pi}{4}) = 1$ і$-\dfrac{\pi}{2} \leq \dfrac{\pi}{4} \leq \dfrac{\pi}{2}$. Таким чином, ми бачимо, що\[\tan^{-1}(\tan(\dfrac{5\pi}{4})) = \tan^{-1}(1) = \dfrac{\pi}{4}\]

Властивості оберненої косинусної функції

Для кожного$t$ в замкнутому інтервалі$[0, \pi]$:\[\cos^{-1}(\cos(t)) = t\]
Для кожного$y$ в замкнутому інтервалі$[-1, 1]$:\[\cos(\cos^{-1}(y)) = y\]

Властивості оберненої тангенсної функції

Для кожного$t$ у відкритому інтервалі$(-\dfrac{\pi}{2}, \pi)$:\[\tan^{-1}(\tan(t)) = t\]
Для кожного дійсного числа$y$:\[\tan(\tan^{-1}(y)) = y\]

Обгрунтування цих властивостей включено в вправи.

Вправа$\PageIndex{4}$

Визначте точне значення кожного з наступних і перевірте їх за допомогою калькулятора.

$y = \arccos(1)$
$y = \tan^{-1}(\sqrt{3})$
$y = \arctan(-1)$
$y = \cos^{-1}(-\dfrac{\sqrt{2}}{2})$
$\sin(\arccos(-\dfrac{1}{2}))$
$\tan(\arcsin(-\dfrac{\sqrt{3}}{2}))$
$\arccos(\sin(\dfrac{\pi}{6}))$

Коли ми оцінюємо вираз, як$\sin(\arccos(-\dfrac{1}{2}))$ у попередньому перегляді діяльності, ми можемо використовувати той факт, що можна визначити точне значення$\arccos(-\dfrac{1}{2})$ для завершення проблеми. Якщо нам дано подібну задачу, але не знаємо точного значення оберненої тригонометричної функції, ми часто можемо використовувати Піфагорійську Ідентичність, щоб допомогти. Ми зробимо це під час наступної перевірки прогресу.

Відповідь

$y = \arccos(1) = 0$
$y = \tan(\sqrt{3}) = \dfrac{\pi}{3}$
$y = \arctan(-1) = -\dfrac{\pi}{4}$
$y = \cos^{-1}(-\dfrac{\sqrt{2}}{2}) = \dfrac{3\pi}{4}$
$\sin(\arccos(\dfrac{1}{2})) = \dfrac{\sqrt{3}}{2}$
$\tan(\arcsin(-\dfrac{\sqrt{3}}{2})) = -\sqrt{3}$
$\arccos(\sin(\dfrac{\pi}{6})) = \dfrac{\pi}{3}$

Вправа$\PageIndex{5}$

Визначте точне значення$\sin(\arccos(\dfrac{1}{3}))$. Нижче наведено запропонований спосіб почати це. Оскільки ми не знаємо точного значення$\arccos(\dfrac{1}{3})$, ми починаємо з дозволу$t = \arccos(\dfrac{1}{3})$. Тоді ми знаємо, що$\cos(t) = \dfrac{1}{3}$ і$0 \leq t \leq \pi$. Зауважте, що$\sin(t) = \sin(\arccos(\dfrac{1}{3}))$. Отже, щоб завершити проблему, визначте точне значення$\sin(t)$ використання Піфагора Ідентичність, маючи на увазі, що$0 \leq t \leq \pi$.
Визначте точне значення$\cos(\arcsin(-\dfrac{4}{7}))$

Відповідь

1. Нехай$t = \arccos(\dfrac{1}{3})$. Тоді ми знаємо, що\[\cos(t) = \dfrac{1}{3}\] і\[0 \leq t \leq \pi\]
Використовуючи Піфагорійську Ідентичність, ми бачимо, що$(\dfrac{1}{3})^{2} + \sin^{2}(t) = 1$ і це означає$\sin^{2}(t) = \dfrac{8}{9}$. Так як$0 \leq t \leq \pi$,$t$ знаходиться у другому квадранті і в обох цих квадрантах,$\sin(t) > 0$. Отже,$\sin(t) = \dfrac{\sqrt{8}}{3}$. Тобто,\ [\ sin (\ arccos (\ dfrac {1} {3})) =\ dfrac {\ sqrt {8}} {3}\).

2. Бо$\cos(\arcsin(-\dfrac{4}{7}))$, ми дозволяємо$t = \arcsin(-\dfrac{4}{7})$. Це означає, що

\[\sin(t) = -\dfrac{4}{7}\]і\[-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}.\]
Ми можемо використовувати Піфагорійську Ідентичність для отримання$\cos^{2}(t) + (-\dfrac{4}{7})^{2} = 1$. Це дає$\cos^{2}(t) = \dfrac{33}{49}$. У нас також є обмеження,$-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}$ і ми знаємо$\sin(t) < 0$. Це означає, що$t$ повинно бути в$QIV$ і так$\cos(t) > 0$. Отже,$\cos(t) = \dfrac{\sqrt{33}}{7}$. Тобто,

\[\cos(\arcsin(-\dfrac{4}{7})) = \dfrac{\sqrt{33}}{7}\]

Примітка: Ви можете скористатися калькулятором, щоб перевірити цю роботу. Використовуйте свій калькулятор, щоб приблизити обидва$\cos(\arcsin(-\dfrac{4}{7}))$ і$\dfrac{\sqrt{33}}{7}$. Обидва результати повинні бути$0.8206518066$.

Резюме

У цьому розділі ми вивчили наступні важливі поняття та ідеї:

Функція зворотного синуса однозначно змінює те, що робить функція синуса. Функція зворотного синуса приймає значення$y$ з діапазону синусоїдальної функції і дає нам рівно одне дійсне число t, синус якого дорівнює$y$. Тобто якщо$y$ є дійсним числом і$-1 \leq y \leq 1$, то$\sin^{-1}(y) = t$ означає, що$\sin(t) = y$ і$-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$. Крім того, функція зворотного синуса задовольняє наступним важливим властивостям:

Для кожного$t$ в замкнутому інтервалі$[-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$,\[\sin^{-1}(\sin(t)) = t\]
Для кожного$y$ в замкнутому інтервалі$[-1, 1]$,\[\sin(\sin^{-1}(y)) = y\]

Функція зворотного косинуса однозначно змінює те, що робить функція косинуса. Функція оберненого косинуса приймає значення$y$ з діапазону функції косинуса і дає нам рівно одне дійсне число, косинус$t$ якого дорівнює$y$. Тобто якщо$y$ є дійсним числом і$-1 \leq y \leq 1$, то$\cos^{-1}(y) = t$ означає, що$\cos(t) = y$ і$0 \leq t \leq \pi$. Крім того, функція зворотного косинуса задовольняє наступним важливим властивостям:

Для кожного$t$ в замкнутому інтервалі$[0, \pi]$,\[\cos^{-1}(\cos(t)) = t\]
Для кожного$y$ в замкнутому інтервалі$[-1, 1]$,\[\cos(\cos^{-1}(y)) = y\]

Функція оберненої дотичної однозначно змінює те, що робить функція дотичної. Зворотна тангенсна функція приймає значення$y$ з діапазону дотичної функції і дає нам рівно одне дійсне число, тангенс$t$ якого дорівнює$y$. Тобто якщо$y$ є дійсним числом, то$\tan^{-1}(y) = t$ означає, що$\tan(t) = y$ і$-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}$. Крім того, функція оберненої дотичної задовольняє таким важливим властивостям:

Для кожного$t$ у відкритому проміжку$(-\dfrac{\pi}{2}, \dfrac{\pi}{2})$,\[\tan^{-1}(\tan(t)) = t\]
Для кожного дійсного числа$y$\[\tan(\tan^{-1}(y)) = y\]