2.E: Графіки тригонометричних функцій (вправи)

Вправа\(\PageIndex{1}\)

У кожному з наступних графіків зліва показана кінцева точка дуги\(t\) (з\(0 \leq t \leq 2\pi\)) на одиничному колі. Графіки праворуч показують графіки\(y = \cos(t)\) та\(y = \sin(t)\) з деякими точками на графіку, позначені. Зіставте точку на графіках\(y = \cos(t)\) і\(y = \sin(t)\) які відповідають точці на одиничному колі. Крім того, вкажіть координати точок на\(y = \cos(t)\) і\(y = \sin(t)\).

(а)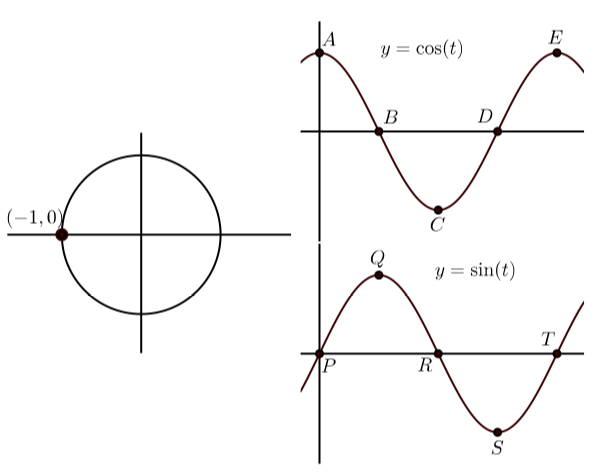

(б)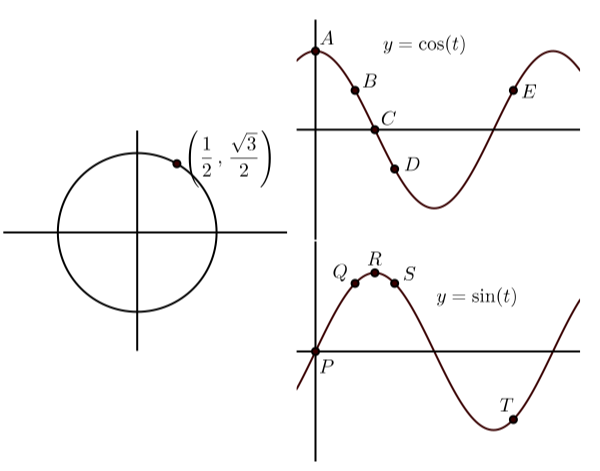

(c)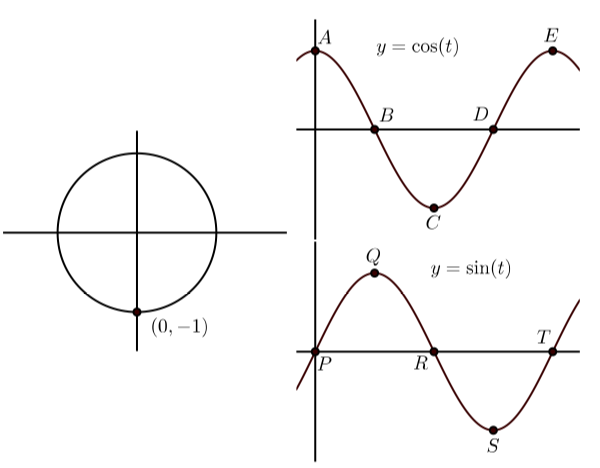

(г)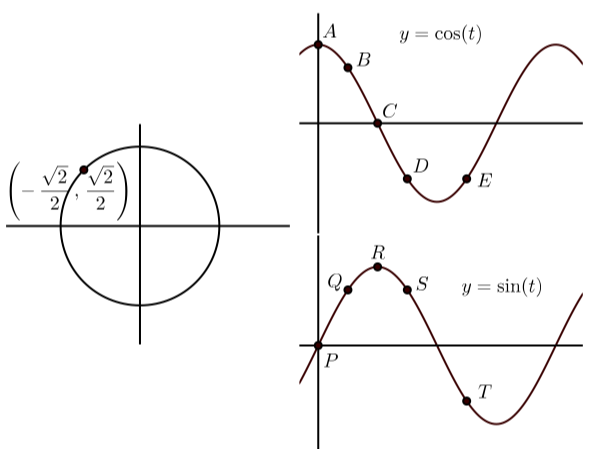

Відповідь

(а)\(C(\pi, -1)\)\(R(\pi, 0)\)

(б)\(B(\dfrac{\pi}{3}, \dfrac{1}{2})\)\(Q(\dfrac{\pi}{3}, \dfrac{\sqrt{3}}{2})\)

Вправа\(\PageIndex{2}\)

Для кожного з наступних визначте рівняння виду\(y = A\cos(t)\) або\(y = A\sin(t)\) для заданого графіка.

(а)

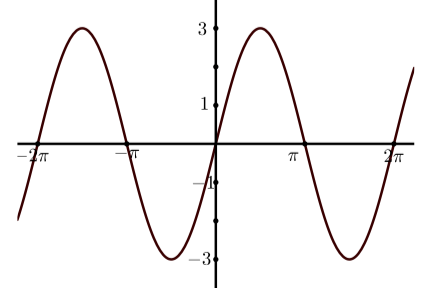
(б)

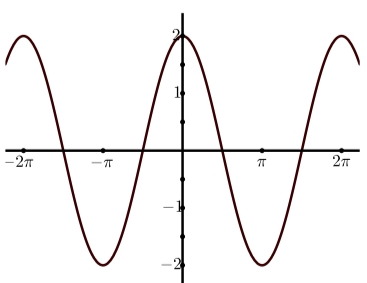
(c)

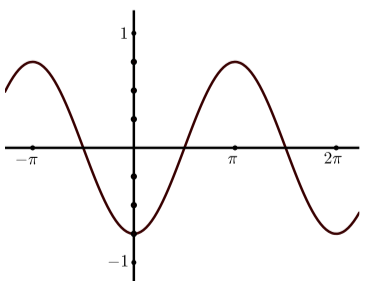
Відповідь

(а)\(y = 3\sin(x)\)

(б)\(y = 2\cos(x)\)

Вправа\(\PageIndex{3}\)

Намалюйте графік кожної з наступних синусоїдальних функцій протягом зазначеного інтервалу. Для кожного графа

• Створіть\(t\) -перехоплення на заданому інтервалі.
• Держава\(y\) -перехоплення.
• Вкажіть максимальне значення функції і координати всіх точок, де відбувається максимальне значення.
• Вкажіть мінімальне значення функції і координати всіх точок, де відбувається мінімальне значення.

1. \(y = \sin(t)\)с\(-2\pi \leq t \leq 2\pi\).
2. \(y = 3\cos(t)\)с\(-\pi \leq t \leq 3\pi\).
3. \(y = 5\sin(t)\)с\(0 \leq t\leq 4\pi\).
4. \(y = \dfrac{3}{7}\cos(t)\)с\(-\pi \leq t \leq 3\pi\).
5. \(y = -2.35\sin(t)\)с\(-\pi \leq t \leq \pi\).
6. \(y = -4\cos(t)\)с\(0 \leq t \leq 6\pi\).

Відповідь

(а)\(t\) -перехоплює:\(-2\pi, -\pi, 0, \pi, 2\pi\),\(y\) -перехоплення:\((0, 0)\)

Максимальне значення -\(1\). Максимальне значення відбувається в точках\((-\dfrac{3\pi}{2}, 1)\) і\((\dfrac{\pi}{2}, 1)\).

Мінімальне значення -\(-1\). Мінімальне значення відбувається в точках\((-\dfrac{\pi}{2}, -1)\) і\((\dfrac{3\pi}{2}, -1)\).

(б)\(t\) -перехоплює:\(-\dfrac{3\pi}{2}, -\dfrac{\pi}{2}, \dfrac{\pi}{2}, \dfrac{3\pi}{2}\),\(y\) -перехоплення:\((0, 2)\)

Максимальне значення -\(2\). Максимальне значення відбувається в точках\((0, 2)\) і\((2\pi, 2)\).

Мінімальне значення -\(-2\). Мінімальне значення відбувається в точках\((-\pi -2)\),\((\pi, -2)\) і\((3\pi, -2)\).

Вправа\(\PageIndex{4}\)

Далі наведено графік трохи більше одного періоду синусоїдальної функції. Шість точок позначені на графіку.

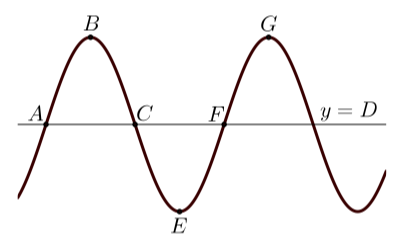
Малюнок\(\PageIndex{1}\)

Для кожної з наступних синусоїдальних функцій:

• Створіть амплітуду, період, зсув фаз та вертикальний зсув.
• Вкажіть координати точок\(A, B, C, E, F\), і\(G\). Так як функції періодичні, існує кілька правильних відповідей. Для цих функцій зробіть\(A\) крапку якомога ближче до початку.

Зверніть увагу, що горизонтальна лінія - це не горизонтальна вісь, а, скоріше, лінія\(y = D\).

\[(a) y = 2\sin(\pi x)\]

\[(b) y = 7.2\cos(2x)\]

\[(c) y = 3\sin(x - \dfrac{\pi}{4})\]

\[(d) y = 3\sin(x + \dfrac{\pi}{4})\]

\[(e) y = 4\cos(x - \dfrac{\pi}{3})\]

\[(f) y = 2.8\cos(2(x - \dfrac{\pi}{3}))\]

\[(g) y = 4\sin(2(x - \dfrac{\pi}{4}))+1\]

\[(h) y = -4\cos(2(x + \dfrac{\pi}{4}))+1\]

\[(i) y = 3\cos(2\pi x - \dfrac{\pi}{2})\]

\[(j) y = -1.75\sin(2x - \dfrac{\pi}{3}) + 2\]

\[(k) y = 5\sin(120\pi x)\]

\[(l) y = 40\sin(50\pi(x - \dfrac{1}{100}))\]

Відповідь

(а)\(y = 2\sin(\pi x)\). Амплітуда є\(2\); період є\(2\); фазовий зсув є\(0\); і вертикальний зсув є\(0\).

\[A(0, 0)\]\[B(\dfrac{\pi}{2}, 2)\]\[C(\pi, 0)\]\[E(\dfrac{3\pi}{2}, -2)\]\[F(2\pi, 0)\]\[G(\dfrac{5\pi}{2}, 2)\]

(c)\(y = 3\sin(x - \dfrac{\pi}{4})\). Амплітуда є\(3\); період є\(2\pi\); фазовий зсув є\(\dfrac{\pi}{4}\); і вертикальний зсув є\(0\).

\[A(\dfrac{\pi}{4}, 0)\]\[B(\dfrac{3\pi}{4}, 3)\]\[C(\dfrac{5\pi}{4}, 0)\]\[E(\dfrac{7\pi}{4}, -3)\]\[F(\dfrac{7\pi}{4}, -3)\]\[G(\dfrac{11\pi}{4}, 3)\]

(г)\(y = 4\sin(2(x - \dfrac{\pi}{4})) + 1\). Амплітуда є\(4\); період є\(\pi\); фазовий зсув є\(\dfrac{\pi}{4}\); і вертикальний зсув є\(1\).

\[A(\dfrac{\pi}{4}, 1)\]\[B(\dfrac{\pi}{2}, 5)\]\[C(\dfrac{3\pi}{4}, 1)\]\[E(\pi, -3)\]\[F(\dfrac{5\pi}{4}, 1)\]\[G(\dfrac{3\pi}{2}, 5)\]

Вправа\(\PageIndex{5}\)

Кожен з наступних графіків являє собою графік синусоїдальної функції. У кожному конкретному випадку:

• Визначити амплітуду синусоїдальної функції.
• Визначте період синусоїдальної функції.
• Визначити вертикальний зсув синусоїдальної функції.
• Визначте рівняння виду\(y = A\sin(B(x - C)) + D\), яке виробляє заданий графік.
• Визначте рівняння виду\(y = A\cos(B(x - C)) + D\), яке виробляє заданий графік.

(а)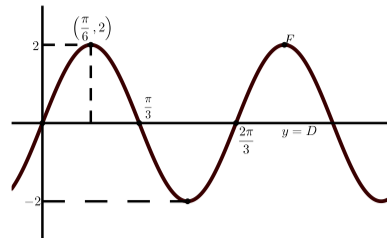

(б)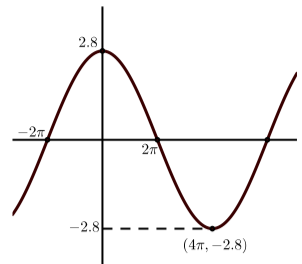

(c)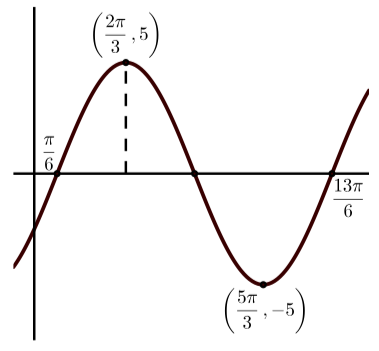

(г)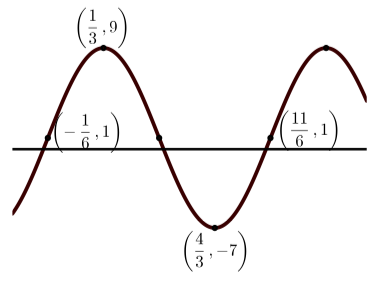

(е)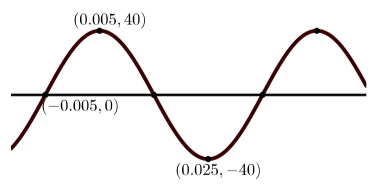

(f)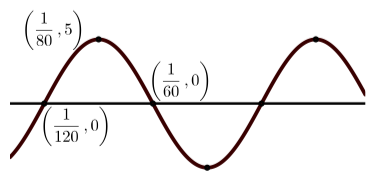

Відповідь

(а) Амплітуда є\(2\); період є\(\dfrac{2\pi}{3}\); і немає вертикального зсуву.

Бо\(y = A\sin(B(x - C)) + D\), немає фазового зсуву і так\(C = 0\). Отже\[y = 2\sin(3x)\]. Бо\(y = A\cos(B(x - C)) + D\), зсув фаз є\(\dfrac{\pi}{6}\) і так\(C = \dfrac{\pi}{6}\). Отже\[y = 2\cos(3(x - \dfrac{\pi}{6}))\].

(d) Амплітуда є\(8\); період є\(2\); і вертикальний зсув є\(1\).

Бо\(y = A\sin(B(x - C)) + D\), зсув фаз є\(-\dfrac{1}{6}\) і так\(C = -\dfrac{1}{6}\). Отже\[y = 8\sin(\pi(x + \dfrac{1}{6}))\]. Бо\(y = A\cos(B(x - C)) + D\), зсув фаз є\(\dfrac{1}{3}\) і так\(C = \dfrac{1}{3}\). Отже\[y = 8\cos(\pi(x - \dfrac{1}{3})) + 1\].

Вправа\(\PageIndex{6}\)

Кожне з наступних веб-посилань є аплетом на Geogebratube. Для кожного з них наведено графік синусоїдальної функції. Мета полягає у визначенні функції форми

\[f(x) = A\sin(B(x - C)) + D\]або\[f(x) = A\cos(B(x - C)) + D\]
як вказано в аплеті. Є поля, які необхідно використовувати для введення значень\(A, B, C\), і\(D\).

1. gvsu.edu/с/09ф
2. gvsu.edu/с/09г
3. http://gvsu.edu/s/09h
4. gvsu.edu/с/09i
5. gvsu.edu/с/09j
6. http://gvsu.edu/s/09k

Вправа\(\PageIndex{7}\)

Визначте амплітуду, період, зсув фаз та вертикальний зсув для кожної з наступних синусоїд. Потім використовуйте цю інформацію для графіка одного повного періоду синусоїди та координат стану високої точки, низької точки та точки, де синусоїда перетинає центральну лінію.

\[(a) y = 4\sin(\pi x - \dfrac{\pi}{8})\]

\[(b) y = 5\cos(4x + \dfrac{\pi}{2}) + 2\]

\[(c) y = -3.2\cos(50\pi x - \dfrac{\pi}{2})\]

\[(d) y = 4.8\sin(\dfrac{1}{4}x + \dfrac{\pi}{8})\]

Додайте сюди текст. Щоб автоматичний номер працював, потрібно додати шаблон «AutoNum» (бажано в кінці) на сторінку.

Відповідь

(а) Пишемо\(y = 4\sin(\pi x - \dfrac{\pi}{8}) = 4\sin(\pi(x - \dfrac{1}{8}))\). Отже, амплітуда є\(4\), період є\(2\), фазовий зсув є\(\dfrac{1}{8}\), і немає вертикального зсуву.

Деякі високі точки на графіку:\((\dfrac{5}{8}, 4)\),\((\dfrac{21}{8}, 4)\). Деякі низькі точки на графіку:\((\dfrac{13}{8}, -4)\),\((\dfrac{29}{8}, -4)\). Графік перетинає центральну лінію за адресою:\((\dfrac{1}{8}, 0)\)\((\dfrac{9}{8}, 0)\),,\((\dfrac{17}{8}, 0)\).

(б) Пишемо\(y = 4\cos(4x + \dfrac{\pi}{2}) + 2 = 5\cos(4(x + \dfrac{\pi}{8})) + 2\). Отже, амплітуда є\(5\), період є\(\dfrac{\pi}{2}\), фазовий зсув є\(-\dfrac{\pi}{8}\), а вертикальний зсув є\(2\).

Деякі високі точки на графіку:\((-\dfrac{\pi}{8}, 7)\),\((\dfrac{3\pi}{8}, 7)\). Деякі низькі точки на графіку:\((\dfrac{\pi}{8}, -3)\),\((\dfrac{5\pi}{8}, -3)\). Графік перетинає центральну лінію за адресою:\((0, 2)\)\((\dfrac{\pi}{4}, 2)\),,\((\dfrac{\pi}{2}, 2)\).

Вправа\(\PageIndex{8}\)

Моделювання серцебиття. Для даної людини в стані спокою припустимо, що серце перекачує кров з регулярною швидкістю близько 75 імпульсів в хвилину. Також припустимо, що обсяг серця цієї людини становить приблизно 150 мілілітрів (мл), і воно з кожним ударом виштовхує приблизно\(54\%\) свій обсяг. Ми будемо моделювати\(V(t)\) обсяг крові (в мілілітрах) в серці в будь-який час\(t\), як синусоїдальну функцію форми\[V(t) = A\cos(Bt) + D\]

1. Якщо ми вибираємо час\(0\), коли серце наповнене кров'ю, чому розумно використовувати функцію косинуса для нашої моделі?
2. Яке максимальне значення\(V(t)\)? Яке мінімальне значення (V (t)\)? Що це говорить нам про значення A і D? Поясніть.
3. Частота простого гармонічного руху - це кількість періодів в одиницю часу, або кількість імпульсів в хвилину в даному прикладі. Як частота f пов'язана з періодом? Яке значення B має мати? Поясніть.
4. Намалюйте графік (без калькулятора) вашого (V (t)\), використовуючи ваші значення A, B та D двох періодів, що починаються з\(t = 0\).
5. Чітко визначте максимальні і мінімальні значення\(V(t)\) на графіку. Що ж говорять нам ці цифри про серце в ці часи?

Відповідь

(б) Максимальне значення -\(150\) мл, а мінімальне значення -\(81\) мл. Таким чином, ми можемо використовувати\(A = \dfrac{150 - 81}{2} = 34.5\) і\(D = \dfrac{150 + 81}{2} = 115.5\).

(c) Період -\(\dfrac{1}{75}\) мін.

Вправа\(\PageIndex{9}\)

Електроенергія, що подається в житлові будинки, називається змінним струмом (AC), оскільки струм змінюється синусоїдально з часом. Напруга, яка викликає струм, також змінюється синусоїдально з часом. У ланцюзі змінного (змінного) струму напруга\(V\) (в вольтах) як функція часу є синусоїдальною функцією виду\[V = V_{0}\sin(2\pi ft)\]

де\(V_{0}\) позитивна константа, а f - частота. Частота - це кількість повних коливань (циклів) в секунду. У Сполучених Штатах це 60 герц (Гц), що означає, що частота становить 60 циклів в секунду.

1. Що таке амплітуда і який період синусоїдальної функції в (1)? Потужність (у ватах), що подається на опір R (в Омах) в будь-який момент t задається\[P = \dfrac{V^2}{R}\]
2. Покажіть, що\(P = \dfrac{V^2}{R}\sin^2(2\pi ft)\)
3. Графік\(P\) як функції часу наведено нижче.

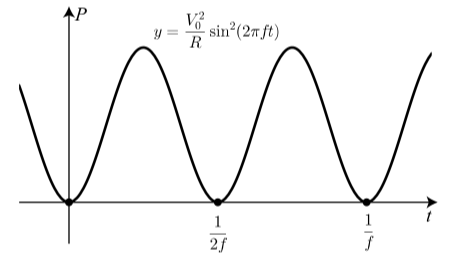
Малюнок\(\PageIndex{2}\)

Припускаючи, що\(P\) це показує, що це синусоїдальна функція t, запишіть\(P\) як синусоїдальну функцію часу,\(t\) використовуючи негатив косинусоїдальної функції без зсуву фази.
4. Таким чином, ми знаємо, що\(P = \dfrac{V_{0}^2}{R}\sin^2(2\pi ft)\) і що P дорівнює синусоїдальної функції в частині (c). Встановіть два вирази для\(P\) рівних один одному і використовуйте отримане рівняння, щоб зробити висновок, що\[sin^2(2\pi ft) = \dfrac{1}{2}[1 - cos(4\pi ft)]\]

Вправа\(\PageIndex{10}\)

Електроенергія, що подається в житлові будинки, називається змінним струмом (AC), оскільки струм змінюється синусоїдально з часом. Напруга, яка викликає струм, також змінюється синусоїдально з часом. І струм, і напруга мають частоту 60 циклів в секунду, але мають різні фазові зсуви. (Примітка: Частота 60 циклів в секунду відповідає\(\dfrac{1}{60}\) періоду в секунду.)

\(C\)Дозволяти струм (в амперах),\(V\) нехай напруга (в вольтах), і нехай t буде час (в секундах). Наступний список дає інформацію, яка відома про\(C\) і\(V\).

• Струм\(C\) - це синусоїдальна функція часу з частотою 60 циклів в секунду, і він досягає свого максимуму в 5 ампер при\(t = 0\) секундах.
• Напруга\(V\) - це синусоїдальна функція часу з частотою 60 циклів в секунду. Як показано на графіках на наступній сторінці,\(V\) «веде» струм в тому сенсі, що він досягає свого максимуму до того, як струм досягне свого максимуму. («Ведучий» відповідає негативному зсуву фаз, а «відставання» відповідає позитивному зсуву фаз.) При цьому напруга V призводить струм на 0,003 секунди, тобто він досягає свого максимуму 0,003 секунди, перш ніж струм досягне свого максимуму.
• Пікова напруга - 180 вольт.
• Немає вертикального зсуву ні на графіку струму, ні на напрузі.

1. Визначити синусоїдальні функції для обох\(C\) і\(V\).
2. Яке напруга, коли струм максимальний?
3. Який струм, коли напруга мінімальна?
4. Який струм, коли напруга дорівнює нулю?

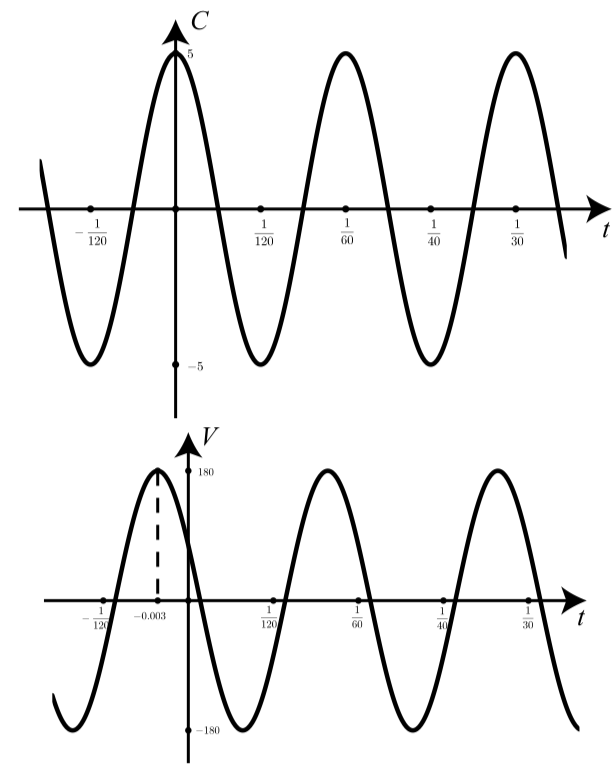
Малюнок\(\PageIndex{3}\): Струм\(C\) і напруга\(V\) як функції часу

Вправа\(\PageIndex{11}\)

Ми дозволимо\(t\) бути номером дня в році. Наступна таблиця показує час сходу сонця (у хвилинах з півночі) для певних днів року в Хоутоні, штат Мічиган.

день	1	31	61	91	121	151	181	211	241	271	301	331	361
час	521	501	453	394	339	304	302	330	369	408	451	494	520

Точки для цієї таблиці побудовані на наступному графіку.

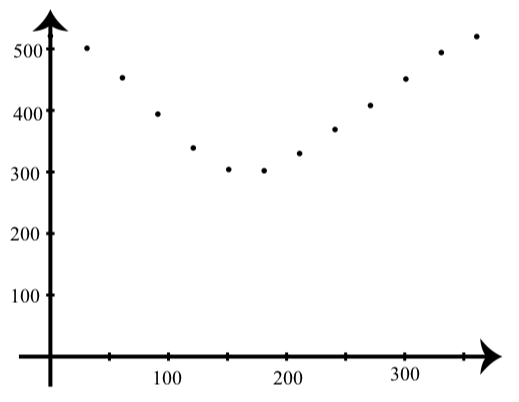
Малюнок\(\PageIndex{4}\)

1. Нехай\(t\) буде номер дня року і нехай\(y\) буде час сходу сонця в хвилинах з півночі в Хоутон, Мічиган. Визначити синусоїдальну модель для\(y\) як функцію\(t\).
2. Щоб перевірити роботу в Part (a), скористайтеся графічною утилітою або Geogebra для побудови точок у таблиці та накладіть графік функції з Part (a).
3. Використовуйте Geogebra для визначення синусоїдальної моделі для\(y\) функції\(t\). Ця модель буде у вигляді\(y = a\sin(bt + c) + d\), де\(a, b, c\), і\(d\) є дійсними числами.
4. Визначте амплітуду, період, фазовий зсув та вертикальний зсув для синусоїдальної моделі в частині (c).

Вправа\(\PageIndex{12}\)

Моделювання відстані від Землі до Сонця.

Орбіта Землі навколо Сонця не є ідеальним колом. У 1609 році Йоганнес Кеплер опублікував два своїх знаменитих закони руху планет, один з яких стверджує, що планетарні орбіти насправді є еліпсами. Так що відстань від Землі до Сонця не є постійною, а змінюється по ходу його орбіти (будемо вважати 365 денний рік). Згідно з ефемеридами США 1996 року, відстані від Сонця до Землі 21-го числа кожного місяця наведені в таблиці 2.3. Відстані вимірюються в астрономічних одиницях (AU), де 1 AU становить приблизно\(149597900\) кілометри.

http://image.gsfc.nasa.gov/poetry/venus/q638.html

Місяць	День року	Відстань
Січень	21	0,9840
Лютий	52	0.9888
Березень	80	0,9962
Квітень	111	1,0050
Травень	141	1.0122
Червень	172	1.0163
Липень	202	1.0161
серпня	233	1.0116
Вересень	264	1,0039
Жовтень	294	0,9954
Листопад	325	0.9878
Грудень	355	0,9837

Таблиця\(\PageIndex{1}\): Відстані від Землі до Сонця 21-го числа кожного місяця

Графік цих даних з днем року по горизонтальній осі і відстанню від Землі до Сонця по вертикальній осі наведено на малюнку\(\PageIndex{5}\).

Ми будемо використовувати синусоїдальну функцію для моделювання цих даних. Тобто ми\(f(t)\) дозволимо відстань від Землі до Сонця в день\(t\) року і що\[f(t) = A\sin(B(t - C)) + D\]

1. Які максимальні і мінімальні відстані від Землі до Сонця задаються даними? Що це говорить нам про амплітуду off.t/? Використовувати це для наближення значень\(A\) і\(D\) в моделі функції\(f\)? Яка центральна лінія для цієї синусоїдальної моделі?
2. Період цієї синусоїдальної функції становить 365 днів. Яке значення\(B\) для цієї синусоїдальної функції?
3. Намалюйте центральну лінію, яку ви знайшли в частині (а) на графіку даних на малюнку\(\PageIndex{5}\). Приблизно при якому значенні\(t\) буде граф фінперетину цієї осьової лінії? Як це число пов'язане з фазовим зсувом даних? Яке значення\(C\) для цієї синусоїдальної функції?
4. Використовуйте Geogebra для побудови точок з даних у таблиці,\(\PageIndex{1}\) а потім використовуйте Geogebra, щоб намалювати графік синусоїдальної моделі\(f(t) = A\sin(B(t - C)) + D\). Чи є ця функція моделює дані досить добре?
5. Використовуйте\(f(t) = A\sin(B(t - C)) + D\) синусоїдальну модель для оцінки відстані від Землі до Сонця 4 липня.

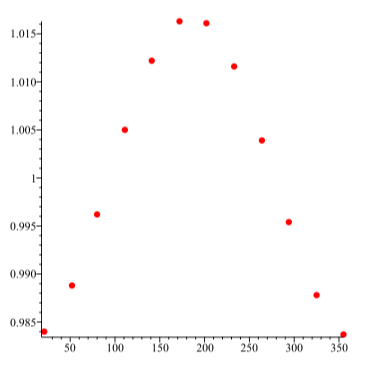
Малюнок\(\PageIndex{5}\): Відстань від Землі до Сонця як функція дня року

Вправа\(\PageIndex{13}\)

Продовження вправи\(\PageIndex{12}\).

Використовуйте Geogebra для побудови точок з даних у таблиці\(\PageIndex{1}\). Потім використовуйте команду «FitSin» в Geogebra, щоб знайти синусоїдальну модель для цих даних форми\(g(t) = a\sin(bt + c) + d\)

Яка амплітуда у цієї синусоїдальної моделі? Що таке період? Що таке горизонтальний зсув? Що таке зсув фаз?

Як ці значення порівнюються з відповідними значеннями для синусоїди,\(f(t) = A\sin(B(t - C)) + D\) отриманих у Вправі (6)?

Вправа\(\PageIndex{14}\)

У міру того, як Місяць обертається навколо землі, зовнішній вигляд Місяця змінюється. Ми бачимо різні місячні диски в різний час місяця. Ці зміни з'являються знову протягом кожного місячного місяця. Однак місячний місяць не зовсім такий, як дванадцять місяців, які ми використовуємо в нашому календарі сьогодні. Місячний місяць - це кількість днів, які потрібно місяцю, щоб пройти один повний цикл від повного місяця (100% освітленості) до наступного повного місяця.

Наступні дані були зібрані з веб-сайту Військово-морської обсерваторії США. Дані представляють собою відсоток Місяця, який освітлюється - це геоцентрична величина відсотка Місяця, яка освітлюється. Тобто відсоток освітленості обчислюється для вигаданого спостерігача, розташованого в центрі Землі.

Дата	Відсоток освітленого
1/3/2013	\(87\%\)
3/3/2013	\(69\%\)
05.03.2017	\(47\%\)
07.03.2017	\(25\%\)
09.03.2017	\(9\%\)
3/12/2013	\(0\%\)
13.03.2013	\(2\%\)
15.03.2017	\(12\%\)
17.03.2013	\(27\%\)
19.03.2013	\(45\%\)
21.03.2013	\(64\%\)
23.03.2013	\(81\%\)
25.03.2013	\(94\%\)
27.03.2013	\(100\%\)
29.03.2013	\(96\%\)

Таблиця\(\PageIndex{2}\)

1. Визначте синусоїдальну функцію форми\(y = A\cos(B(t - C)) + D\) для моделювання цих даних. Для цієї функції, нехай x - кількість днів з початку березня 2017 року і нехай y - відсоток місяця, який освітлюється. Що таке амплітуда, період, зсув фаз та вертикальний зсув цієї синусоїдальної функції?
2. Використовуйте Geogebra, щоб намалювати графік розкиду цих даних і накласти графік функції з частини (a).
3. Використовуйте Geogebra для визначення синусоїдальної функції форми\(y = A\sin(Bx + K) + D\) для моделювання цих даних та накладення його графіка на графік розсіювання. Що таке амплітуда, період, зсув фаз та вертикальний зсув цієї синусоїдальної функції?

Вправа\(\PageIndex{15}\)

Кожне з наступних веб-посилань є аплетом на Geogebratube. Для кожного з них наносяться дані, а в деяких випадках фактичні дані відображаються в електронній таблиці праворуч. Мета полягає у визначенні функції форми

\[f(x) = A\sin(B(x- C)) + D\]або\[f(x) = A\cos(B(x- C)) + D\]

який максимально щільно підходить до даних. У кожному аплеті буде вказано тип функції, яку слід використовувати. Є поля, які необхідно використовувати для введення значень\(A, B, C\), і\(D\).

1. ГВСУ.еду/с/09л
2. http://gvsu.edu/s/09m
3. http://gvsu.edu/s/09n
4. http://gvsu.edu/s/09o

Вправа\(\PageIndex{16}\)

У цій вправі ми вивчимо період дотичної функції.

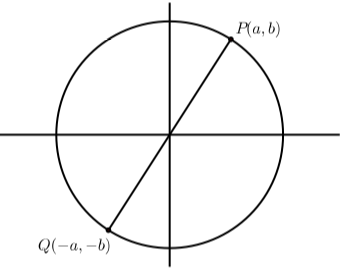
Малюнок\(\PageIndex{6}\)

1. Використовують визначення тангенсної функції і той факт, що період як синусоїдних, так і косинусних функцій дорівнює\(2\pi\) довести, що для будь-якого дійсного числа t в області дотичної функції,\[\tan(t + 2\pi) = \tan(t)\] Однак це не доводить, що період дотичної функції дорівнює\(2\pi\). Ми зараз покажемо, що період дорівнює\(\pi\). Ключем до доказу є схема праворуч. Припустимо, що\(P\) це кінцева точка дуги\(t\). Так\(\cos(t) = a\) і\(\sin(t) = b\). На діаграмі показана точка Q, яка є кінцевою точкою дуги\(t + \pi\). За симетрією кола ми знаємо, що точка\(Q\) має координати\((-a, -b)\).
2. Поясніть, чому\(\cos(t + \pi) = -a\) і\(\sin(t + \pi) = -b\)
3. Використовуйте інформацію в частині (1) та визначення тангенсної функції, щоб довести це\(\tan(t + \pi) = \tan(t)\).

На діаграмі також зазначено, що найменша позитивна величина,\(p\) для якої\(\tan(t + p) = \tan(t)\) має бути\(p = \pi\). Значить, період, якому дотична функція дорівнює\(\pi\).

Вправа\(\PageIndex{17}\)

Ми бачили, що\(\cos(-t) = \cos(t)\) і\(\sin(-t) = \sin(t)\) для кожного реального числа\(t\). Тепер припустимо, що\(t\) це дійсне число, для\(\tan(t)\) якого визначено.

1. Скористайтеся визначенням тангенсної функції, щоб написати формулу для\(\tan(-t)\) через\(\sin(-t)\) і\(\cos(-t)\).
2. Тепер використовуйте негативні тотожності дуги для функцій косинуса та синуса, щоб допомогти довести це\(\tan(-t) = -\tan(t)\). Це називається від'ємною дуговою ідентичністю для тангенсної функції.
3. Використовуйте від'ємну ідентичність дуги для функції дотичної\(y = \tan(t)\), щоб пояснити, чому граф симетричний щодо походження.

Вправа\(\PageIndex{18}\)

Використовуйте від'ємні ідентичності дуги для синуса, косинуса та тангенса, щоб допомогти довести наступні негативні ідентичності дуги для косеканси, секанси та котангенса.

1. Для кожного дійсного числа,\(t\) для якого\(t \neq k\pi\) для кожного цілого числа\(k\),\(\csc(-t) = -\csc(t)\).
2. Для кожного дійсного числа,\(t\) для якого\(t \neq \dfrac{\pi}{2} + k\pi\) для кожного цілого числа\(k\),\(\sec(-t) = \sec(t)\).
3. Для кожного дійсного числа,\(t\) для якого\(t \neq k\pi\) для кожного цілого числа\(k\),\(\cot(-t) = -\cot(t)\).

Вправа\(\PageIndex{19}\)

Функція косеканс.

Якщо необхідно, зверніться до розділу 1.6, щоб відповісти на наступні запитання.

1. Як визначається функція косеканса?
2. Яка область функції косеканса?
3. Де граф косекансної функції матиме вертикальні асимптоти?
4. Що таке період косекансної функції?

Вправа\(\PageIndex{20}\)

Вивчення графіка косекансної функції.

1. Використовуйте аплет Geogebra з наступною веб-адресою, щоб вивчити взаємозв'язок між графіком функції косеканса та функцією синуса. http://gvsu.edu/s/0bH В аплеті графік\(y = \sin(t)\) показаний і залишається фіксованим. Точки на графіку\(y = \csc(t)\) генеруються за допомогою повзунка для\(t\). Для кожного значення\(t\) з проводиться вертикальна лінія від точки\((t, \sin(t))\) до точки\((t, \csc(t))\). Зверніть увагу, як ці точки вказують на те, що графік косекансної функції має вертикальні асимптоти при\(t = 0, t = \pi\) і\(t = 2\pi\).
2. Використовуйте графічну утиліту, щоб намалювати графік\(y = \csc(t)\) використання\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\) та\(-10 \leq y \leq 10\). Примітка: Можливо, доведеться використовувати\(\csc(x) = \dfrac{1}{\sin(x)}\)
3. Використовуйте графічну утиліту, щоб намалювати графік\(y = \csc(t)\) використання\(-\dfrac{3\pi}{2} \leq x \leq \dfrac{3\pi}{2}\) та\(-10 \leq y \leq 10\).

Вправа\(\PageIndex{21}\)

Графік косекансної функції.

1. Чому графік\(y = \csc(t)\) має вертикальні асимптоти при\(x = 0, x = \pi\), і\(x = 2\pi\)? Яка область функції косеканса?
2. Чому граф\(y = \csc(t)\) вище осі х, коли\(0 < x < \pi\)?
3. Чому граф\(y = \csc(t)\) вище осі х, коли\(\pi < x < 2\pi\)?
4. Що таке діапазон косекансної функції?

Вправа\(\PageIndex{22}\)

Функція котангенса.

Якщо необхідно, зверніться до розділу 1.6, щоб відповісти на наступні запитання.

1. Як визначається функція котангенса?
2. Яка область котангенса функції?
3. Де граф котангенсної функції матиме вертикальні асимптоти?
4. Що таке період котангенсної функції?

Вправа\(\PageIndex{23}\)

Вивчення графіка функції котангенса.

1. Використовуйте графічну утиліту, щоб намалювати графік\(y = \cot(x)\) використання\(-\pi \leq x \leq \pi\) та\(-10 \leq y \leq 10\). Примітка: Можливо, доведеться використовувати\(\cot(x) = \dfrac{1}{tan(x)}\).
2. Використовуйте графічну утиліту, щоб намалювати графік\(y = \cot(x)\) використання\(-2\pi \leq x \leq 2\pi\) та\(-10 \leq y \leq 10\).

Вправа\(\PageIndex{24}\)

Графік функції котангенса.

1. Чому графік\(y = \cot(t)\) має вертикальні асимптоти при\(x = 0, x = \pi\), і\(x = 2\pi\)? Яка область функції косеканса?
2. Чому графік\(y = \cot(t)\) вище осі х коли\(0 < x < \dfrac{\pi}{2}\) і коли\(\pi < x < \dfrac{3\pi}{2}\)?
3. Чому графік\(y = \cot(t)\) вище осі х коли\(\dfrac{\pi}{2} < x < \pi\) і коли\(\dfrac{3\pi}{2} < x < 2\pi\)?
4. Який діапазон котангенсної функції?

Вправа\(\PageIndex{25}\)

Перепишіть кожне з наступних, використовуючи відповідну тригонометричну функцію для оберненої тригонометричної функції. Потім визначте точне значення оберненої тригонометричної функції.

\[(a) t = \arcsin(\dfrac{\sqrt{2}}{2})\]

\[(b) t = \arcsin(-\dfrac{\sqrt{2}}{2})\]

\[(c) t = \arccos(\dfrac{\sqrt{2}}{2})\]

\[(d) t = \arccos(-\dfrac{\sqrt{2}}{2})\]

\[(e) y = \tan^{-1}(\dfrac{\sqrt{3}}{2})\]

\[(f) y = \tan^{-1}(\dfrac{-\sqrt{3}}{2})\]

\[(g) y = \cos^{-1}(0)\]

\[(h) t = \arctan(0)\]

\[(i) y = \sin^{-1}(-\dfrac{1}{2})\]

\[(j) y = \cos^{-1}(-\dfrac{1}{2})\]

Відповідь

(а)\(t = \arcsin(\dfrac{\sqrt{2}}{2})\) означає\(\sin(t) = \dfrac{\sqrt{2}}{2}\) і\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\). З тих пір\(\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\), ми це бачимо\(t = \arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\).

(б)\(t = \arcsin(-\dfrac{\sqrt{2}}{2})\) означає\(\sin(t) = -\dfrac{\sqrt{2}}{2}\) і\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\). З тих пір\(\sin(\dfrac{-\pi}{4}) = -\dfrac{\sqrt{2}}{2}\), ми це бачимо\(t = \arcsin(\dfrac{\sqrt{2}}{2}) = -\dfrac{\pi}{4}\).

(г)\(t = \arccos(-\dfrac{\sqrt{2}}{2})\) означає\(\cos(t) = -\dfrac{\sqrt{2}}{2}\) і\(0 \leq t \leq \pi\). З тих пір\(\cos(\dfrac{3\pi}{4}) = -\dfrac{\sqrt{2}}{2}\), ми це бачимо\(t = \arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{3\pi}{4}\).

(f)\(y = \tan^{-1}(-\dfrac{\sqrt{3}}{3})\) означає\(\tan(y) = -\dfrac{\sqrt{3}}{3}\) і\(-\dfrac{\pi}{2} < y < \dfrac{\pi}{2}\). З тих пір\(\tan(-\dfrac{\pi}{6}) = -\dfrac{\sqrt{3}}{3}\), ми це бачимо\(y = \tan^{-1}(-\dfrac{\sqrt{3}}{2}) = -\dfrac{\pi}{6}\).

(ч)\(t = \arctan(0) = 0\)

(j)\(y = \cos^{-1}(-\dfrac{1}{2}) = \dfrac{2\pi}{3}\).

Вправа\(\PageIndex{26}\)

Визначте точне значення кожного з наступних виразів.

\[(a) \sin(\sin^{-1}(1))\]

\[(b) \sin^{-1}(\sin(\dfrac{\pi}{3}))\]

\[(c) \cos^{-1}(\sin(\dfrac{\pi}{3}))\]

\[(d) \sin^{-1}(\sin(-\dfrac{\pi}{3}))\]

\[(e) \cos^{-1}(\cos(-\dfrac{\pi}{3}))\]

\[(f) \arcsin(\sin(\dfrac{2\pi}{3}))\]

\[(g) \tan(\arctan(1))\]

\[(h) \arctan(\tan(\dfrac{\pi}{4}))\]

\[(i) \arctan(\tan(\dfrac{3\pi}{4}))\]

Відповідь

(а)\(\sin(\sin^{-1}(1)) = \sin(\dfrac{\pi}{2}) = 1\)

(б)\(\sin^{-1}(\sin(\dfrac{\pi}{3})) = \sin^{-1}(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\)

(е)\(\cos^{-1}(\cos(-\dfrac{\pi}{3})) = \cos^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{3}\)

(f)\(\arcsin(\sin(\dfrac{2\pi}{3})) = \arcsin(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\)

(i)\(\arctan(\tan(\dfrac{3\pi}{4})) = \arctan(-1) = -\dfrac{\pi}{4}\)

Вправа\(\PageIndex{27}\)

Визначте точне значення кожного з наступних виразів.

\[(a) \cos(\arcsin(\dfrac{2}{5}))\]

\[(b) \sin(\arccos(-\dfrac{2}{3}))\]

\[(c) \tan(\arcsin(\dfrac{1}{3}))\]

\[(d) \cos(\arcsin(-\dfrac{2}{5}))\]

\[(e) \tan(\arccos(-\dfrac{2}{9}))\]

Відповідь

(а) Нехай\(t = \arcsin(\dfrac{2}{5})\). Потім\(\sin(t) = \dfrac{2}{5}\) і\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\), і

\[\cos^{2}(t) + \sin^{2}(t) = 1\]

\[\cos^{2}(t) + \dfrac{4}{25} = 1\]

\[\cos^{2}(t) = \dfrac{21}{25}\]

Так як\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\), ми це знаємо\(\cos(t) \geq 0\). Значить,\(\cos(t) = \dfrac{\sqrt{21}}{5}\) і\(\cos(\arcsin(\dfrac{2}{5})) = \dfrac{\sqrt{21}}{5}\).

(б)\(\sin(\arccos(-\dfrac{2}{3})) = \dfrac{\sqrt{5}}{3}\).

(c)\(\tan(\arcsin(\dfrac{1}{3})) = \dfrac{1}{\sqrt{8}}\).

Вправа\(\PageIndex{28}\)

Ця вправа надає обґрунтування властивостей функції оберненого косинуса на сторінці 150. \(t\)Дозволяти дійсне число в замкнутому інтервалі\([0, \pi]\) і нехай\[y = \cos(t).\] Ми потім бачимо, що\(-1 \leq y \leq 1\) і\[\cos^{-1}(y) = t\]

1. Використовуйте рівняння, щоб переписати вираз\(\cos^{-1}(\cos(t))\).
2. Використовуйте рівняння, щоб переписати вираз\(\cos(\cos^{-1}(y))\).

Вправа\(\PageIndex{29}\)

Ця вправа дає обґрунтування властивостей функції оберненого косинуса на сторінці 151. \(t\)Дозволяти дійсне число у відкритому інтервалі\((-\dfrac{\pi}{2}, \dfrac{\pi}{2})\) і нехай\[y = \tan(t).\] ми потім бачимо, що\(y\) це дійсне число і\[\tan^{-1}(y) = t\]

1. Використовуйте рівняння, щоб переписати вираз\(\tan^{-1}(\tan(t))\).
2. Використовуйте рівняння, щоб переписати вираз\(\tan(\tan^{-1}(y))\).

Вправа\(\PageIndex{30}\)

Для кожного з наступних рівнянь використовуйте графік, щоб наблизити розв'язки (до трьох десяткових знаків) рівняння на вказаному інтервалі. Потім використовуйте періодичну властивість тригонометричної функції для написання формул, які можуть бути використані для наближення будь-якого розв'язку даного рівняння.

1. \(\sin(x) = 0.75\)з\(-\pi \leq x \leq \pi\)
2. \(\cos(x) = 0.75\)з\(-\pi \leq x \leq \pi\)
3. \(\tan(x) = 0.75\)з\((-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2})\)
4. \(\sin(x) = -0.75\)з\(-\pi \leq x \leq \pi\)
5. \(\cos(x) = -0.75\)з\(-\pi \leq x \leq \pi\)
6. \(\tan(x) = -0.75\)з\((-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2})\)

Відповідь

(a)\(x = 0.848 + k(2\pi)\) або\(x = 2.294 + k(2\pi)\), де\(k\) ціле число.

(d)\(x = -0.848 + k(2\pi)\) або\(x = -2.294 + k(2\pi)\), де\(k\) ціле число.

Вправа\(\PageIndex{31}\)

Для кожного з рівнянь у Вправі (1) використовуйте обернену тригонометричну функцію, щоб записати точні значення всіх розв'язків рівняння на вказаному інтервалі. Потім використовуйте періодичну властивість тригонометричної функції для написання формул, які можуть бути використані для генерації всіх розв'язків даного рівняння.

Відповідь

(a)\(x = \sin^{-1}(0.75) + k(2\pi)\) або\(x = (\pi - \sin^{-1}(0.75)) + k(2\pi)\), де\(k\) ціле число.

(d)\(x = \arcsin(-0.75) + k(2\pi)\) або\(x = (\pi - \arcsin(-0.75)) + k(2\pi)\), де\(k\) ціле число.

Вправа\(\PageIndex{32}\)

Для кожного з рівнянь наступних рівнянь використовуйте обернену тригонометричну функцію, щоб записати точні значення всіх розв'язків рівняння на вказаному інтервалі. Потім використовуйте періодичну властивість тригонометричної функції для написання формул, які можуть бути використані для генерації всіх розв'язків даного рівняння.

1. \(\sin(x) + 2 = 2.4\)з\(-\pi \leq x \leq \pi\)
2. \(5\cos(x) + 3 = 7\)з\(-\pi \leq x \leq \pi\)
3. \(2\tan(x) + 4 = 10\)з\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\)
4. \(-3.8\sin(x) + 7 = 10\)з\(-\pi \leq x \leq \pi\)
5. \(8\cos(x) + 7 = 2\)з\(-\pi \leq x \leq \pi\)

Відповідь

(a)\(x = \sin^{-1}(0.4) + k(2\pi)\) або\(x = (\pi - \sin^{-1}(0.4)) + k(2\pi)\), де\(k\) ціле число.

(b)\(x = \cos^{-1}(\dfrac{4}{5}) + k(2\pi)\) або\(x = -\cos^{-1}(\dfrac{4}{5}) + k(2\pi)\), де\(k\) ціле число.

Вправа\(\PageIndex{33}\)

Визначте точні значення розв'язків даного рівняння на одному повному періоді тригонометричної функції, яка використовується в рівнянні. Потім використовуйте періодичну властивість тригонометричної функції для написання формул, які можуть бути використані для всіх розв'язків даного рівняння.

1. \(4\sin(2x) = 3\)
2. \(4\cos(2x) = 3\)
3. \(\cos(\pi x) = 0.6\)
4. \(\sin(\pi x - \dfrac{\pi}{4}) = 0.2\)
5. \(\cos(\pi x - \dfrac{\pi}{4}) = 0.2\)

Відповідь

(а) Період для тригонометричної функції дорівнює\(\pi\). Спочатку вирішуємо рівняння\(4\sin(t) = 3\) с\(-\pi \leq t \leq \pi\) і отримуємо\(t = \sin^{-1}(0.75) + k(2\pi)\) або\(t = (\pi - \sin^{-1}(0.75)) + k(2\pi)\). Потім ми використовуємо підстановку\(t = 2x\) для отримання\(x = \dfrac{1}{2}\sin^{-1}(0.75) + k\pi\) або\(x = \dfrac{1}{2}(\pi - \sin^{-1}(0.75)) + k\pi\), де\(k\) ціле число.

(d) Період для тригонометричної функції дорівнює\(2\). Спочатку вирішуємо рівняння\(\sin(t) = 0.2\) с\(-\pi \leq t \leq \pi\) і отримуємо\(t = \sin^{-1}(0.2) + k(2\pi)\) або\(t = (\pi - \sin^{-1}(0.2)) + k(2\pi)\). Тепер ми використовуємо підстановку\(t = \pi x - \dfrac{\pi}{4}\) для отримання\(x = \dfrac{1}{\pi}\sin^{-1}(0.2) + \dfrac{1}{4}\) або\(x = -\dfrac{1}{\pi} + \dfrac{5}{4}) + 2k\), де\(k\) ціле число.

Вправа\(\PageIndex{34}\)

У прикладі 2.17 на сторінці 2.17 ми використовували графічні методи для пошуку двох розв'язків рівняння\[35\cos(\dfrac{5\pi}{3}t) + 105 = 100\]

Ми виявили, що два рішення були\(t \approx 0.3274\) і\(t \approx 0.8726\). Перепишіть це рівняння, а потім скористайтеся функцією зворотного косинуса, щоб визначити точні значення цих двох розв'язків. Потім використовуйте період функції\(35\cos(\dfrac{5\pi}{3}t) + 105\) для написання формул, які можуть бути використані для генерації всіх розв'язків даного рівняння.