2.4: Графіки інших тригонометричних функцій

Фокусні питання

Наступні питання призначені для керівництва нашим вивченням матеріалу в цьому розділі. Вивчивши цей розділ, ми повинні зрозуміти поняття, мотивовані цими питаннями, і вміти писати точні, узгоджені відповіді на ці питання.

• Які важливі властивості графіка\(y = \tan(t)\). Тобто, що таке область і який діапазон дотичної функції, і що відбувається зі значеннями тангенсної функції в точках, які знаходяться поблизу точок не в області дотичної функції?
• Які важливі властивості графіка\(y = \sec(t)\). Тобто, що таке область і який діапазон функції секанс, і що відбувається зі значеннями функції секанс в точках, які знаходяться поблизу точок не в області секантної функції?
• Які важливі властивості графіка\(y = \cot(t)\). Тобто, що таке область і який діапазон котангенсної функції, і що відбувається зі значеннями функції котангенса в точках, які знаходяться поблизу точок не в області функції котангенса?
• Які важливі властивості графіка\(y = \csc(t)\). Тобто, що таке домен і який діапазон косекансної функції, і що відбувається зі значеннями функції косеканс в точках, які знаходяться поблизу точок не в області функції косеканса?

Ми бачили, як визначаються графіки функцій косинуса і синуса за визначенням цих функцій. Ми також досліджували ефекти констант\(A, B, C\), а\(D\) на графіку\(y = A\sin(B(x - C)) + D\) і графік\(y = A\sin(B(x - C)) + D\).

На наступному початку діяльності ми вивчимо графік тангенсної функції. Пізніше в цьому розділі ми обговоримо графік секансної функції, а графіки котангенсної і косекансної функцій будуть вивчені у вправах. Однією з ключових особливостей цих графіків є той факт, що всі вони мають вертикальні асимптоти. Важлива інформація про всі чотири функції узагальнена в кінці цього розділу.

Початок діяльності

1. Використовуйте графічну утиліту, щоб намалювати графік\(f(x) = \dfrac{1}{(x+1)(x-1)}\) використання\(-2 \leq x \leq 2\) та\(-10 \leq y \leq 10\). Якщо можливо, скористайтеся утилітою графіків, щоб намалювати графіки вертикальних ліній\(x = -1\) і\(x = 1\). Графік функції\(f\) має вертикальні асимптоти\(x = -1\) і\(x = 1\). Причина цього полягає в тому\(x\), що при цих значеннях чисельник функції не дорівнює нулю, а знаменник дорівнює 0. Так\(x = -1\) і\(x = 1\) знаходяться не в області цієї функції. Загалом, якщо функція є часткою двох функцій, то буде вертикальна асимптота для тих значень x, для яких чисельник не дорівнює нулю, а знаменник дорівнює нулю. Ми побачимо це для тангенс, котангенс, секанс і косеканс функцій.
2. Як визначається функція дотичної? Виконайте наступне: Для кожного дійсного числа\(x\) с\(\cos(t) \neq 0, \tan(t) = ?\).
3. Використовуйте графічну утиліту, щоб намалювати графік\(y = \tan(t)\) використання\(-\pi \leq t \leq \pi\) та\(-10 \leq y \leq 10\).
4. Які вертикальні асимптоти графа функції\(y = \tan(t)\)? Що, здається, є діапазоном дотичної функції?

Графік тангенсної функції

Графік тангенсної функції сильно відрізняється від графіків синусоїдних і косинусних функцій. Одна з причин полягає в тому\(\tan(t) = \dfrac{\sin(t)}{\cos(t)}\), що, існують значення\(t\) для яких\(\tan(t)\) не визначено. Ми бачили, що область дотичної функції - це множина всіх дійсних чисел,\(t\) для яких\(t = \neq \dfrac{\pi}{2} + k\pi\) для кожного цілого числа\(k\).

Зокрема, дійсні числа\(\dfrac{\pi}{2}\) і не\(-\dfrac{\pi}{2}\) знаходяться в області дотичної функції. Таким чином, графік тангенсної функції матиме вертикальні асимптоти при\(t = \dfrac{\pi}{2}\) і\(t = -\dfrac{\pi}{2}\) (як і при інших значеннях). Ми повинні були спостерігати це на початку діяльності.

Так що, щоб намалювати точний графік дотичної функції, потрібно буде зрозуміти поведінку дотичної біля точок, які не знаходяться в її області. Зараз ми досліджуємо поведінку тангенса для точок\(t\), значення яких трохи менше, ніж\(\dfrac{\pi}{2}\) і для точок, значення t яких трохи більше\(-\dfrac{\pi}{2}\). За допомогою калькулятора ми можемо отримати значення, наведені в таблиці 2.4.

\(t\)	\(\tan(t)\)
\ (t\) ">\(\dfrac{\pi}{2} - 0.1\)	\ (\ тан (т)\) ">9.966644423
\ (t\) ">\(\dfrac{\pi}{2} - 0.01\)	\ (\ тан (т)\) ">99.99666664
\ (t\) ">\(\dfrac{\pi}{2} - 0.001\)	\ (\ тан (т)\) ">999.9996667
\ (t\) ">\(\dfrac{\pi}{2} - 0.0001\)	\ (\ тан (т)\) ">9999.999967
\ (t\) ">\(\dfrac{\pi}{2} + 0.1\)	\ (\ тан (т)\) ">-9.966644423
\ (t\) ">\(\dfrac{\pi}{2} + 0.01\)	\ (\ тан (т)\) ">-99.99666664
\ (t\) ">\(\dfrac{\pi}{2} + 0.001\)	\ (\ тан (т)\) ">-999.9996667
\ (t\) ">\(\dfrac{\pi}{2} + 0.0001\)	\ (\ тан (т)\) ">-9999.999967

Таблиця 2.4: Таблиця значень для тангенсної функції

Таким чином, як вхід\(t\) наближається до\(\dfrac{\pi}{2}\) але залишається менше\(\dfrac{\pi}{2}\), ніж, значення\(\tan(t)\) стають все більше і більше, здавалося б, без обмежень. Аналогічно, вхід\(t\) наближається до\(-\dfrac{\pi}{2}\),\(-\dfrac{\pi}{2}\) але залишається більшим, значення tan.t/стають все далі і далі від 0 в негативному напрямку, здавалося б, без обмежень. Ми бачимо це у визначенні дотичної: як\(t\) наближається\(\dfrac{\pi}{2}\) до ліворуч,\(\cos(t)\) наближається до 0 і\(\sin(t)\) наближається до 1. Тепер\(\tan(t) = \dfrac{\sin(t)}{\cos(t)}\) і дроби, де чисельник близький до\(1\) і знаменник близький до\(0\) мають дуже великі значення. Точно так само, як t наближається\(-\dfrac{\pi}{2}\) до праворуч,\(\cos(t)\) наближається до\(0\) (але є негативним) і\(\sin(t)\) наближається до\(1\). Дроби, де чисельник близький до 1, а знаменник близький до 0, але негативний, є дуже великими (за величиною) від'ємними числами.

Вправа\(\PageIndex{1}\)

1. Використовуйте графічну утиліту, щоб намалювати графік\(y = \tan(t)\) використання\(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\) та\(-10 \leq y \leq 10\).
2. Використовуйте графічну утиліту, щоб намалювати графік\(y = \tan(t)\) використання\(-\dfrac{3\pi}{2} \leq t \leq \dfrac{3\pi}{2}\) та\(-10 \leq y \leq 10\).
3. Чи відповідають ці графіки інформації, яку ми обговорювали про вертикальні асимптоти для тангенсної функції?
4. Що, здається, є діапазоном дотичної функції?
5. Що, здається, є періодом дотичної функції?

Відповідь

Графіки для (1) та (2) наведені нижче.

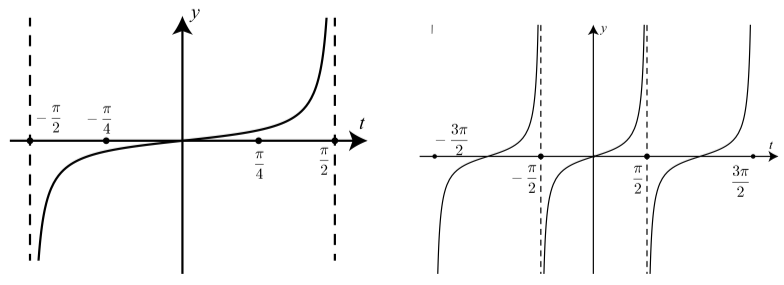
На обох графіках графік зліва\(t = \dfrac{\pi}{2}\) і праворуч від\(t = -\dfrac{\pi}{2}\) відповідає інформації в таблиці 2.4. Графік на

право також узгоджується з інформацією в цій таблиці по обидва боки\(t = \dfrac{\pi}{2}\) і\(t = -\dfrac{\pi}{2}\)

Діапазон функції дотичної - це множина всіх дійсних чисел.

На основі графіка в (2) видається період дотичної функції\(\pi\). Період фактично дорівнює\(\pi\), і більше інформації про це наведено у Вправі (1).

Діяльність 2.22 (Функція дотичної та одиничне коло)

Діаграма на малюнку\(\PageIndex{1}\) може бути використана для того, щоб показати, як\(\tan(t)\) пов'язано з одиничним кругом визначень\(\cos(t)\) і\(\sin(t)\).

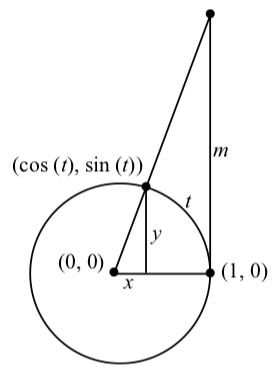
Малюнок\(\PageIndex{1}\): Ілюстрація за\(\tan(t)\) допомогою одиничного кола

На схемі малюється дуга довжиною t і\(\tan(t) = \dfrac{\cos(t)}{\sin(t)} = \dfrac{y}{x}\). Це дає нахил лінії, яка проходить через точки\((0, 0)\) і\((\cos(t), \sin(t))\). Вертикальна лінія через точку\((1, 0)\) перетинає цю пряму в точці\((1, m)\). Це означає, що нахил цієї лінії також m і, отже, ми бачимо, що\[\tan(t) = \dfrac{\cos(t)}{\sin(t)} = m.\]

Тепер використовуйте генератор дотичних графіків аплету Geogebra, щоб побачити, як ця інформація може бути використана, щоб побачити, як графік функції дотичної може бути створений за допомогою ідей на малюнку\(\PageIndex{1}\). Веб-адреса http://gvsu.edu/s/Zm

Вплив констант на графи тангенсної функції

Є подібності і деякі відмінності в методах малювання графіка функції форми\(y = A\tan(B(t - C)) + D\) і креслення графіка функції форми\(y = A\sin(B(t - C)) + D\). Див. сторінку 101 для зведення ефектів параметрів\(A, B, C\), а також\(D\) на графіку синусоїдальної функції.

Однією з відмінностей у роботі з дотичною (сікантною, котангенсною або косекансною) функцією є те, що ми не використовуємо термінологію, специфічну для синусоїдальних хвиль. Зокрема, ми не будемо використовувати терміни амплітуда і фазовий зсув. Замість амплітуди ми використовуємо більш загальний термін вертикальне розтягування (або вертикальне стиснення), а замість фазового зсуву використовуємо більш загальний термін горизонтальний зсув. Ми вивчимо це наступну перевірку прогресу.

Вправа\(\PageIndex{2}\)

Розглянемо функцію, рівняння якої є\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\). Навіть якщо ми використовуємо графічну утиліту для малювання графіка, ми повинні спочатку відповісти на наступні питання, щоб отримати розумне вікно перегляду для графічної утиліти. Це може бути гарною ідеєю, щоб використовувати метод, подібний до того, що ми б використовувати, якби ми були графіки\(y = 3\sin(2(x - \dfrac{\pi}{8})) + 1\)

1. Ми знаємо, що для синусоїди період є\(\dfrac{2\pi}{2}\). Однак період дотичної функції є\(\pi\). Так яким буде період\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\)?
2. Для синусоїди амплітуда дорівнює 3. Однак ми не використовуємо термін «амплітуда» для дотичної. Так в чому ж полягає вплив параметра 2 на графіку\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\)?
3. Для синусоїди фазовий зсув дорівнює\(\dfrac{\pi}{8}\). Однак ми не використовуємо термін «зсув фаз» для дотичної. Так в чому ж полягає вплив параметра 8 на графіку\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\)?
4. Використовуйте утиліту графіків, щоб намалювати графік цієї функції протягом одного повного періоду. Використовуйте період функції, яка містить число 0.

Відповідь

1. Рівняння для функції\(y = 3\tan(2(x - \dfrac{\pi}{8})) + 1\)
2. Період виконання цієї функції дорівнює\(\dfrac{\pi}{2}\).
3. Ефект параметра\(3\) полягає в вертикальному розтягуванні графіка дотичної функції.
4. Далі наведено графік одного періоду цієї функції з використанням\(-\dfrac{\pi}{8} \leq x \leq \dfrac{3\pi}{8}\) і\(-20 \leq y \leq 20\). Показані вертикальні\(x = -\dfrac{\pi}{8}\)\(x = \dfrac{3\pi}{8}\) асимптоти в, а також горизонтальна лінія\(y = 1\).

• Ефект від параметра\(\dfrac{\pi}{8}\) полягає в зміщенні графіка\(y = 3\tan(2(x)) + 1\) вправо на\(\dfrac{\pi}{8}\) одиниці.

Графік функції секанс

Щоб зрозуміти графік секансної функції, потрібно згадати визначення секанса і обмеження на її область. Якщо необхідно, зверніться до розділу 1.6, щоб завершити наступну перевірку прогресу.

Вправа\(\PageIndex{3}\)

1. Як визначається функція секанс?
2. Яка область функції секанс?
3. Де граф секантної функції матиме вертикальні асимптоти?
4. Що таке період секантної функції?

Відповідь

Функція секанс - це зворотна функції косинуса. Тобто,\(\sec(t) = \dfrac{1}{\cos(t)}\)

Домен функції secant є множиною всіх дійсних чисел,\(t\) для яких\(t \neq \dfrac{\pi}{2} + k\pi\) для кожного цілого числа\(k\).

Графік секантної функції матиме вертикальну асимптоту при тих значеннях\(t\), яких немає в області. Таким чином, буде вертикальна асимптота, коли\(t = \dfrac{\pi}{2} + k\pi\) для деякого цілого числа\(k\).

Оскільки\(\sec(t) = \dfrac{1}{\cos(t)}\), і період функції косинуса є\(2\pi\), робимо висновок, що період секансної функції теж є\(2\pi\).

Діяльність 2.25 (Графік секантної функції)

Ми будемо використовувати аплет Geogebra з наступною веб-адресою: http://gvsu.edu/s/Zn Цей аплет покаже, як графік секантної функції пов'язаний з графіком функції косинуса. В аплеті графік\(y = \cos(t)\) показаний і залишається фіксованим. Ми генеруємо точки на графіку\(y = \sec(t)\) за допомогою повзунка для t Для кожного значення\(t\), вертикальна лінія проводиться від точки\((t, \cos(t))\) до точки\((t, \sec(t))\). Зверніть увагу, як ці точки вказують на те, що графік секантної функції має вертикальні асимптоти при\(t = \dfrac{\pi}{2}, t = \dfrac{3\pi}{2}\) і\(\dfrac{5\pi}{2}\).

• Використовуйте графічну утиліту, щоб намалювати графік\(y = \sec(t)\) використання\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\) та\(-10 \leq y \leq 10\). Примітка: Можливо, доведеться використовувати\(\sec(x) = \dfrac{1}{\cos(x)}\)
• Використовуйте графічну утиліту, щоб намалювати графік\(y = \sec(t)\) використання\(-\dfrac{3\pi}{2} \leq x \leq \dfrac{3\pi}{2}\) та\(-10 \leq y \leq 10\).
• Робота в Діяльність 2.25 та Рисунок\(\PageIndex{2}\) може бути використана, щоб допомогти відповісти на запитання у Вправи\(\PageIndex{3}\).

  

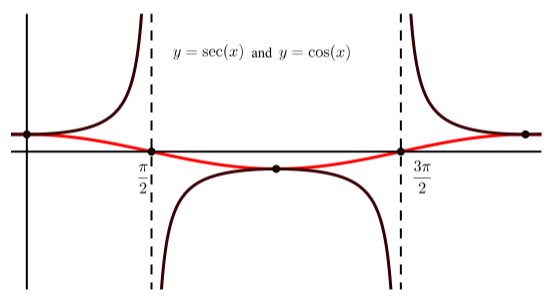
  Малюнок\(\PageIndex{2}\): Графік одного періоду\(y = \sec(t)\) з\(0 \ leq x \ leq 2\pi\)

Вправа\(\PageIndex{4}\)

1. Чи\(\PageIndex{2}\) відповідає графік на малюнку графікам з Діяльності 2.25?
2. Чому граф\(y = \sec(t)\) вище осі х, коли\(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\)?
3. Чому графік\(y = \sec(t)\) нижче осі х, коли\(\dfrac{\pi}{2} \leq x \leq \dfrac{3\pi}{2}\)
4. Який діапазон функції секанс?

Відповідь

Всі графіки узгоджені.

З тих пір\(\sec(x) = \dfrac{1}{\cos(x)}\), ми бачимо, що\(\sec(x) > 0\) якщо і тільки якщо\(\cos(x) > 0\). Таким чином, графік\(y = \sec(x)\) знаходиться вище\(x\) -осі, якщо і тільки якщо графік\(y = \cos(x)\) знаходиться вище\(x\) -осі.

3. З тих пір\(\sec(x) = \dfrac{1}{\cos(x)}\), ми бачимо, що\(\sec(x) < 0\) якщо і тільки якщо\(\cos(x) < 0\). Таким чином, графік\(y = \sec(x)\) знаходиться нижче\(x\) -осі, якщо і тільки якщо графік\(y = \cos(x)\) знаходиться вище\(x\) -осі.

Ключ у тому, що\(\sec(x) = \dfrac{1}{\cos(x)}\). Так як\(-1 \leq \cos(x) \leq 1\), робимо висновок, що\(\sec(x) \geq 1\) коли\(\cos(x) > 0\) і\(\sec(x) \leq -1\) коли\(\cos(x) < 0\). Оскільки графік секантної функції має вертикальні асимптоти, ми бачимо, що діапазон функції секанс складається з усіх дійсних чисел,\(y\) для яких\(y \geq 1\) або\(y \leq -1\). Це також можна побачити на графіку\(y = \sec(x)\).

Резюме

У цьому розділі ми вивчили наступні важливі поняття та ідеї:

Функція дотичної. У таблиці 2.5 наведені деякі важливі характеристики функції дотичної. Ми вже обговорювали більшість цих пунктів, але останні два пункти цієї таблиці будуть вивчені у Вправи (1) та Вправа (2). Графік трьох періодів дотичної функції показаний на рис\(\PageIndex{3}\).

	\(y = \tan(t)\)	\(y = \sec(t)\)
період	\(\pi\)	\(2\pi\)
домен	дійсні числа\(t\) з\(t \neq \dfrac{\pi}{2}+k\pi\) для кожного цілого\(k\)	дійсні числа\(t\) з\(t \neq \dfrac{\pi}{2}+k\pi\) для кожного цілого\(k\)
\(y\)-перехопити	\((0, 0)\)	\((0, 1)\)
\(x\)-перехоплює	\(t = k\pi\), де\(k\) деяке ціле число	жоден
симетрія	стосовно походження	по відношенню до\(y\) -осі

Таблиця 2.5: Властивості функцій дотичної та секансної

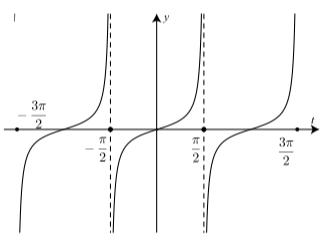
Малюнок\(\PageIndex{3}\): Графік\(y = \tan(t)\)

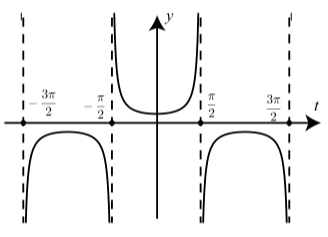
Малюнок\(\PageIndex{4}\): Графік\(y = \sec(t)\)

Функція «Секанс». У таблиці 2.5 наведені деякі важливі характеристики січної функції. Симетрія сікантної функції досліджується у Вправі (3). На малюнку 2.29 показаний графік секантної функції.

Функція косеканс. Графік косекансної функції вивчається таким чином, як ми вивчали графік секансної функції. Це робиться в Вправи (4), (5) і (6). У таблиці 2.6 наведені деякі важливі характеристики функції косеканса. Симетрія косекансної функції досліджується у Вправі (3). На малюнку 2.30 показаний графік функції косеканса.

Функція котангенса. Графік косекансної функції вивчається таким чином, як ми вивчали графік тангенсної функції. Це робиться в Вправи (7), (8) і (9). У таблиці 2.6 наведені деякі важливі характеристики функції котангенса. Симетрія котангенсної функції досліджується у Вправі (3). На малюнку 2.31 показаний графік котангенсної функції.

	\(y = \csc(t)\)	\(y = \cot(t)\)
період	\ (y =\ csc (t)\) ">\(2\pi\)	\ (y =\ cot (t)\) ">\(\pi\)
домен	\ (y =\ csc (t)\) ">дійсні числа\(t\) з кожним\(t \neq k\pi\) цілим числом\(k\)	\ (y =\ cot (t)\) ">дійсні числа\(t\) з кожним\(t \neq k\pi\) цілим числом\(k\)
діапазон	\ (y =\ csc (t)\) ">\(|y| \geq 1\)	\ (y =\ cot (t)\) ">всі дійсні числа
\(y\)-перехопити	\ (y =\ csc (t)\) ">немає	\ (y =\ cot (t)\) ">немає
\(x\)-перехоплює	\ (y =\ csc (t)\) ">немає	\ (y =\ cot (t)\) ">\(t = \dfrac{\pi}{2}+k\pi\) де\(k\) ціле число
симетрія	\ (y =\ csc (t)\) ">щодо походження	\ (y =\ cot (t)\) ">щодо походження

Таблиця 2.6: Властивості косекансної та котангенсної функцій

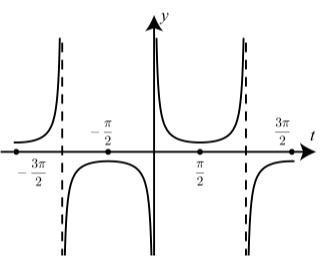
Малюнок\(\PageIndex{5}\): Графік\(y = \csc(t)\)

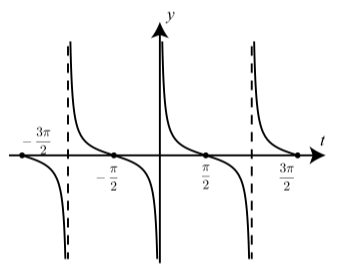
Малюнок\(\PageIndex{6}\): Графік\(y = \cot(t)\)