2.3: Застосування та моделювання з синусоїдальними функціями

Фокусні питання

Наступні питання призначені для керівництва нашим вивченням матеріалу в цьому розділі. Вивчивши цей розділ, ми повинні зрозуміти поняття, мотивовані цими питаннями, і вміти писати точні, узгоджені відповіді на ці питання.

Дозволяти\(A, B, C\), і\(D\) бути константи з\(B > 0\) і розглянути графік\(f(t) = A\sin(B(t - C)) + D\) або\(f(t) = A\cos(B(t - C)) + D\).

• Що означає частота?
• Як ми точно моделюємо періодичні дані за допомогою синусоїдальної функції?
• Що таке математична модель?
• Чому доцільно використовувати синусоїдальну функцію для моделювання періодичних явищ?

У розділі 2.2 ми використовували діаграму на малюнку,\(\PageIndex{1}\) щоб допомогти запам'ятати важливі факти про синусоїдальні функції.

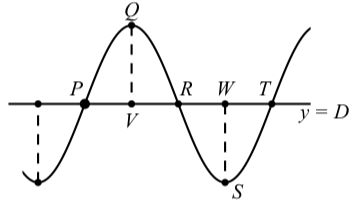
Малюнок\(\PageIndex{1}\): Графік синусоїди

Наприклад:

• Горизонтальна відстань між точкою, де відбувається максимум, і наступною точкою, де відбувається мінімум (наприклад, точки\(Q\) і\(S\)) становить половину періоду. Це довжина відрізка від\(V\) до\(W\) на рис\(\PageIndex{1}\).
• Вертикальна відстань між точкою, де відбувається мінімум (наприклад, точка\(S\)) і точкою, де відбувається максимум (наприклад, точка\(Q\)) дорівнює двократній амплітуді.
• Центральна лінія\(y = D\) для синусоїди знаходиться на півдорозі між максимальним значенням в точці\(Q\) і мінімальним значенням в точці\(S\). Значення\(D\) можна знайти, обчисливши середнє значення\(y\) -координат цих двох точок.
• Горизонтальна відстань між будь-якими двома послідовними точками на лінії\(y = D\) на малюнку\(\PageIndex{1}\) становить одну чверть періоду.

У Progress Check 2.16 ми будемо використовувати деякі з цих фактів, щоб допомогти визначити рівняння, яке буде моделювати об'єм крові в серці людини як функцію часу. Математична модель - це функція, яка описує якесь явище. Для об'єктів, які проявляють періодичну поведінку, в якості моделі може використовуватися синусоїдальна функція, оскільки ці функції є періодичними. Однак поняття частоти використовується в деяких додатках періодичних явищ замість періоду.

Визначення

Частота синусоїдальної функції - це кількість періодів (або циклів) в одиницю часу.

Типовою одиницею частоти є герц. Один герц (Гц) - це один цикл в секунду. Цей підрозділ названий на честь Генріха Герца (1857 — 1894).

Оскільки частота - це кількість циклів за одиницю часу, а період - це кількість часу для завершення одного циклу, ми бачимо, що частота та період пов'язані наступним чином:

\[frequency = \dfrac{1}{period}.\]

Вправа\(\PageIndex{1}\)

Обсяг середнього серця становить 140 мілілітрів (мл), і воно з кожним ударом виштовхує приблизно половину свого обсягу (70 мл). Крім того, частота серцебиття для добре тренованого спортсмена для добре тренованого спортсмена становить 50 ударів (циклів) в хвилину. Ми будемо моделювати обсяг, V .t/(в мілілітрах) крові в серці як функцію часу t вимірюється в секундах. Будемо використовувати синусоїдальну функцію виду\[V(t) = A\cos(B(t - C)) + D\]

Якщо ми виберемо час 0 хвилин, щоб бути часом, коли об'єм крові в серці максимальний (серце наповнене кров'ю), то розумно використовувати функцію косинуса для нашої моделі, оскільки функція косинуса досягає максимального значення, коли її вхід дорівнює 0 і тому ми можемо використовувати\(C = 0\), що відповідає фазі зсув 0. Таким чином, наша функція може бути записана як\(V(t) = A\cos(Bt) + D\).

1. Яке максимальне значення\(V(t)\)? Яке мінімальне значення\(V(t)\)? Використовувати ці значення для визначення значень\(A\) і\(D\) для нашої моделі? Поясніть.
2. Так як частота ударів серця становить 50 ударів в хвилину, ми знаємо, що час на одне серцебиття складе 1 хвилину. Визначте час (в 50 секунд), необхідний для завершення одного серцебиття (циклу). Це період для цієї синусоїдальної функції. Використовуйте цей період для визначення значення Б. Напишіть формулу для\(V(t)\) використання значень\(A, B, C\), і\(D\) які були визначені.

Відповідь

Максимальне значення\(V(t)\) дорівнює\(140\) мл, а мінімальне значення\(V(t)\) -\(70\) мл. Так що різниця\((140 - 70 = 70)\) в два рази перевищує амплітуду. Значить, амплітуда є\(35\) і ми будемо використовувати\(A = 35\). Центральна лінія тоді буде\(35\) одиницями нижче максимуму. Тобто,\(D = 140 - 35 = 105\).

Так як в хвилину трапляються\(50\) удари, то період становить\(\dfrac{1}{50}\) хвилину. Оскільки ми використовуємо секунди для часу, то період -\(\dfrac{60}{50}\) секунди або\(\dfrac{6}{5}\) сек. Ми можемо визначити\(B\), вирішивши рівняння\[\dfrac{2\pi}{B} = \dfrac{6}{5}\] для\(B\). Це дає\(B = \dfrac{10\pi}{6} = \dfrac{5\pi}{3}\). Наша функція

\[V(t) = 35\cos(\dfrac{5\pi}{3}t) + 105.\]

Приклад\(\PageIndex{1}\):

(Продовження перевірки прогресу 2.16)

Тепер, коли ми визначили, що\[V(t) = 35\cos(\dfrac{5\pi}{3}t) + 105\]

(Де\(t\) вимірюється в секундах з моменту заповнення серця і\(V(t)\) вимірюється в мілілітрах) - це модель для кількості крові в серці, ми можемо використовувати цю модель для визначення інших значень, пов'язаних з кількістю крові в серці. Наприклад:

Ми можемо визначити кількість крові в серці за\(1\) секунду після того, як серце було заповнене за допомогою\(t = 1\). \[V(1) = 35\cos(\dfrac{5\pi}{3}) + 105\]Так що можна сказати, що за\(1\) секунду після того, як серце наповниться, в серці будуть\(122.5\) мілілітри крові.

Аналогічним чином, через\(4\) секунди після того, як серце сповнене крові, в серці будуть\(87.5\) мілілітри крові, оскільки\[V(4) = 35\cos(\dfrac{20\pi}{3}) + 105 \approx 87.5\]

Припустимо, що ми хочемо знати, в які моменти після того, як серце наповниться, що в серці буде 100 мілілітрів крові. Ми можемо визначити це, якщо ми зможемо вирішити рівняння\(V(t) = 100\) для\(t\). Тобто нам потрібно вирішити рівняння\[35\cos(\dfrac{5\pi}{3}t) + 105 = 100\]

Хоча інші методи вирішення цього типу рівняння ми дізнаємося пізніше в книзі, ми можемо використовувати графічну утиліту для визначення наближених розв'язків для цього рівняння. \(\PageIndex{2}\)На малюнку показані графіки\(y = V(t)\) і\(y = 100\). Для вирішення рівняння нам потрібно використовувати графічну утиліту, яка дозволяє визначити або наблизити точки перетину двох графіків. (Це можна зробити за допомогою більшості калькуляторів Texas Instruments та Geogebra.) Ідея полягає в тому, щоб знайти координати точок\(P, Q\), і\(R\) на рис\(\PageIndex{2}\).

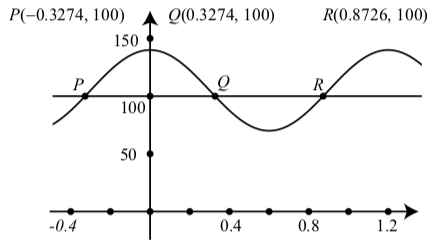
Малюнок\(\PageIndex{2}\): Графік\(V(t) = 35\cos(\dfrac{5\pi}{3}) + 105\) і\(y = 100\)

Нам дійсно потрібно лише знайти координати однієї з цих точок, оскільки ми можемо використовувати властивості синусоїдів, щоб знайти інші. Наприклад, ми можемо визначити, що координати\(P\) є\((-0.3274, 100)\). Тоді, використовуючи той факт, що графік симетричний щодо осі y, ми знаємо координати\(Q\) є\((0.3274, 100)\).\(y = V(t)\) Потім ми можемо використовувати періодичну властивість функції, щоб визначити\(t\) -координату\(R\) шляхом додавання одного періоду до\(t\) -координати\(P\). Це дає\(0.3274 + \dfrac{6}{5} = 0.8726\) і координати\(R\) є\((0.8726, 100)\). Ми також можемо використовувати властивість peredious, щоб визначити стільки розв'язків рівняння\(V(t) = 100\), скільки нам подобається.

Вправа\(\PageIndex{2}\)

Літнє сонцестояння в 2014 році припало на 21 червня, а зимове сонцестояння - 21 грудня. Максимальний світловий день припадає на літнє сонцестояння і мінімальний світловий день припадає на зимове сонцестояння. За даними веб-сайту Військово-морської обсерваторії США, AA.usno.navy.mil/data/docs/dur_oneyear.php,

кількість годин світлового дня в Гранд-Рапідс, штат Мічиган на 21 червня 2014 року склало 15.35 годин, а кількість світлових годин на 21 грудня 2014 року становило 9,02 години. Це означає, що в Гранд-Рапідс,

• Максимальна кількість годин світлового дня становила\(15.35\) годин і припала на день\(172\) року.
• Мінімальна кількість годин світлового дня становила\(9.02\) годин і припала на день\(355\) року.

1. Нехай\(y\) буде кількість годин денного світла в 2014 році в Гранд-Рапідс і нехай\(t\) буде днем року. Визначте синусоїдальну модель за кількістю годин денного світла\(y\) в 2014 році в Гранд-Рапідсі як функція\(t\).

2. Відповідно до цієї моделі,

• (а) Скільки годин денного світла було 10 березня 2014 року?
• (б) У які дні року було 13 годин денного світла?

Відповідь

1. Оскільки у нас є координати для високої та низької точки, ми спочатку робимо такі обчислення:

\(2(amp) = 15.35 - 9.02 = 6.33\). Значить, амплітуда є\(3.165\).

\[D = 9.02 + 3.165 = 12.185\].

\(\dfrac{1}{2}\)період\(= 355 - 172 = 183\). Так і період є\(366\). Зверніть увагу, що ми зазвичай говоримо, що є\(365\) дні в році. Так що також було б розумно використовувати період\(365\) днів. Використовуючи період\(366\) днів, ми виявляємо, що\[\dfrac{2\pi}{B} = 366\]

а значить\(B = \dfrac{\pi}{183}\).

Тепер ми повинні вирішити, чи використовувати функцію синуса або функцію косинуса, щоб отримати фазовий зсув. Оскільки у нас є координати високої точки, ми будемо використовувати функцію косинуса. Для цього зсув фаз складе 172. Таким чином, наша функція

\[y = 3.165\cos(\dfrac{\pi}{183}(t - 172)) + 12.185\]

Ми можемо перевірити це, перевіривши, що коли\(t = 155, y = 15.135\) і що коли\(t = 355, y = 9.02\).

(а) Березень\(10\) - номер дня\(69\). Так використовуємо\(t = 69\) і отримуємо\[y = 3.165\cos(\dfrac{\pi}{183}(69 - 172)) + 12.185 \approx 11.5642\]

Так 10 березня 2014 року було близько\(11.564\) світлового дня.

(b) Ми використовуємо графічну утиліту для наближення точок перетину\(y = 3.165\cos(\dfrac{\pi}{183}(69 - 172)) + 12.125\) і\(y = 13\). Результати показані праворуч. Так на 96-й день (6 квітня 2014 року) і на 248 день (5 вересня) було близько 13 годин світлового дня.

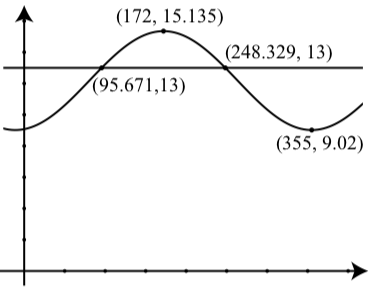
Визначення синусоїди за даними

У процесі перевірки 2.18 значення і час для максимального і мінімального годин денного світла. Навіть якщо ми знаємо, що якесь явище є періодичним, ми можемо не знати значень максимуму і мінімуму. Наприклад, наступна таблиця показує кількість світлових годин (округлених до найближчих сотих часток години) на перше число місяця для Единбурга, Шотландія\((55^\circ 57' N, 3^\circ 12' W)\).

Ми будемо використовувати синусоїдальну функцію форми\(y = A\sin(B(t - C)) + D\), де\(y\) кількість годин денного світла і час,\(t\) виміряний в місяцях для моделювання цих даних. Ми будемо використовувати 1 січня, 2 лютого і т.д. в якості першої спроби ми будемо використовувати\(17.48\) для максимальних годин денного світла і\(7.08\) для мінімальних годин денного світла.

Січ	лют.	бер.	Квітень	Травень	Червень	Липень	серп.	вересня	Жовт	Лис	Груд
7.08	8.60	10.73	13.15	15.40	17.22	17.48	16.03	13.82	11.52	9.18	7.40

Таблиця 2.2: Години денного світла в Единбурзі

• Так як\(17.48 - 7.08 = 10.4\), ми бачимо, що амплітуда дорівнює 5,2 і так\(A = 5.2\).
• Вертикальний зсув буде\(7.08 + 5.2 = 12.28\) і так\(D = 12.28\).
• Термін становить 12 місяців і так\(B = \dfrac{2\pi}{12} = \dfrac{\pi}{6}\).
• Максимум відбувається при\(t = 7\). Для синусоїдальної функції максимальним є одна чверть періоду від часу, коли функція синуса перетинає свою горизонтальну вісь. Це вказує на зсув фаз на 4 вправо. Отже\(C = 4\).

Тож ми будемо використовувати функцію\(y = 5.2\sin(\dfrac{\pi}{6}(t - 4)) + 12.28\) для моделювання кількості годин денного світла. \(\PageIndex{3}\)На малюнку показана діаграма розкиду даних і графік цієї функції. Хоча графік досить добре підходить для даних, здається, ми повинні бути в змозі знайти кращу модель. Одна з проблем полягає в тому, що максимальна кількість годин світлового дня не відбувається 1 липня. Ймовірно, це відбувається приблизно на 10 днів раніше. Мінімум також не відбувається 1 січня і, ймовірно, дещо менше, ніж 7,08 годин. Тож ми спробуємо максимум 17,50 годин і мінімум 7, 06 годин. Крім того, замість того, щоб мати максимум відбувається в\(t = 7\), ми скажемо, що це відбувається в t D 6:7. Використовуючи ці значення, ми маємо\(A = 5.22, B = \dfrac{\pi}{6}, C = 3.7, \space and \space D = 12.28\). На малюнку 2.22 показаний графік розкиду даних і графік\[y = 5.22\sin(\dfrac{\pi}{6}(t - 3.7)) + 12.28\]

Це, здається, дуже добре моделює дані. Важливо відзначити, що при спробі визначити синусоїду, яка «підходить» або моделює фактичні дані, немає єдиної правильної відповіді. Нам часто доводиться знаходити одну модель, а потім використовувати наше судження, щоб визначити кращу модель. Існує математичне рівняння «найкраще підходить» для синусоїди, яке називається рівнянням синусоїди регресії. Зверніть увагу, що нам потрібно використовувати деяку утиліту графіки або програмне забезпечення, щоб отримати рівняння синусоїдної регресії. Багато калькулятори Texas Instruments мають таку особливість, як і програмне забезпечення Geogebra. Нижче наведено рівняння синусоїдної регресії для кількості годин денного світла в Единбурзі, показане в таблиці 2.2, отриманої з Geogebra.

\[y = 5.153\sin(0.511t - 1.829) + 12.174\]

Графік розкиду з графіком цієї функції показаний на малюнку\(\PageIndex{5}\).

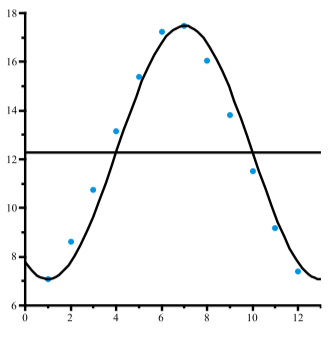
Малюнок\(\PageIndex{3}\): Години денного світла в Единбурзі

Примітка

Дивіться додатки в кінці цього розділу для інструкцій щодо використання Geogebra та Texas Instruments TI-84 для визначення рівняння синусоїдної регресії для заданого набору даних.

Цікаво порівняти рівняння (1) та рівняння (2), обидва з яких є моделями для даних у таблиці 2.2. Ми бачимо, що обидва рівняння мають подібну амплітуду і подібний вертикальний зсув, але зауважте, що рівняння (2) не в нашій стандартній формі для рівняння синусоїди. Тож ми не можемо відразу сказати, що це рівняння говорить про період та фазовий зсув. У цій наступній діяльності ми дізнаємося, як визначити період і фазовий зсув для синусоїдів, рівняння яких мають форму\(y = a\sin(bt + c) + d\) або\(y = a\cos(bt + c) + d\).

Діяльність 2.19 (Робота з синусоїдами, які не в стандартній формі)

Поки що ми працювали з синусоїдами, рівняння яких мають форму\(y = A\sin(B(t - C)) + D\) або\(y = A\cos(B(t - C)) + D\). Коли написано в такому вигляді, ми можемо використовувати значення\(A, B, C\), і\(D\) визначити амплітуду,

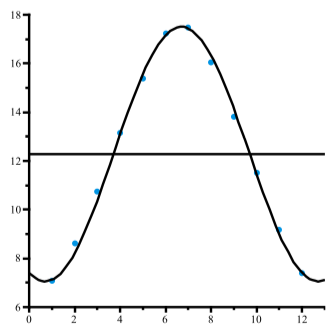
Малюнок\(\PageIndex{4}\): Години денного світла в Единбурзі

період, зсув фаз і вертикальний зсув синусоїди. Ми завжди повинні пам'ятати, однак, що для цього рівняння має бути записано саме в такому вигляді. Якщо у нас є рівняння в дещо іншій формі, ми повинні визначити, чи є спосіб використовувати алгебру для перезапису рівняння у вигляді\(y = A\sin(B(t - C)) + D\) або\(y = A\cos(B(t - C)) + D\). Розглянемо рівняння\(y = 2\sin(3t + \dfrac{\pi}{2})\)

• Використовуйте утиліту графіків, щоб намалювати графік цього рівняння за допомогою\(-\dfrac{\pi}{3} \leq t \leq \dfrac{2\pi}{3} \) і. Це здається графіком синусоїди? Якщо так, чи можете ви використовувати графік, щоб знайти його амплітуду, період, фазовий зсув та вертикальний зсув?
• Можна перевірити будь-які спостереження, які були зроблені за допомогою невеликої алгебри, щоб записати це рівняння у вигляді\(y = A\sin(B(t - C)) + D\). Ідея полягає в тому, щоб переписати аргумент функції синуса, який є\(3t + \dfrac{\pi}{2}\) шляхом «факторингу 3» з обох термінів. Це може здатися трохи дивним, оскільки ми не звикли використовувати дроби при факторі. Наприклад, досить легко врахувати,\(3y + 12\) як\[3y + 12 = 3(y + 4)\]
• Для того, щоб «множити» три від\(\dfrac{\pi}{2}\), ми в основному використовуємо той факт, що\(3 \cdot \dfrac{1}{3} = 1\)

  

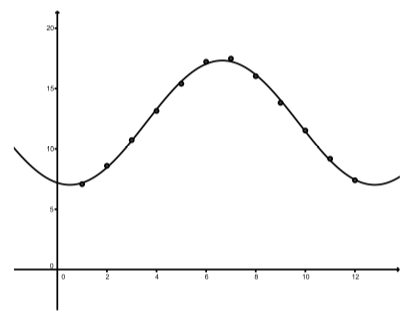
  Малюнок\(\PageIndex{5}\): Години денного світла в Единбурзі

  Таким чином, ми можемо написати\[\dfrac{\pi}{2} = 3 \cdot \dfrac{1}{3} \cdot \dfrac{\pi}{6} = 3 \cdot \dfrac{\pi}{6}\]

  Тепер перепишіть\(3t + \dfrac{\pi}{2}\) факторингом 3, а потім перепишіть\(y = 2\sin(3t + \dfrac{\pi}{2})\) у форму\(y = A\sin(B(t - C)) + D\).

  3. Для чого потрібна амплітуда, період, зсув фаз та вертикальний зсув\(y = 2\sin(3t + \dfrac{\pi}{2})\)?

  У діяльності 2.19 ми зробили невеликий факторинг, щоб показати, що\[y = 2\sin(3t + \dfrac{\pi}{2}) = 2\sin(3(t + \dfrac{\pi}{6}))\]\[y = 2\sin(3(t - (-\dfrac{\pi}{6})))\]

  Таким чином, ми бачимо, що у нас є синусоїдальна функція і що амплітуда 3, період 2, фазовий зсув є\(\dfrac{2\pi}{3}\), а вертикальний зсув дорівнює 0.
  Загалом, ми можемо бачити, що якщо\(b\) і\(c\) є дійсними числами, то\[bt + c = b(t + \dfrac{c}{b}) = b(t - (-\dfrac{c}{d}))\]

  Це означає, що\[y = a\sin(bt + c) + d = a\sin(b(t - (-\dfrac{c}{d}))) + d\]

  Отже, ми маємо наступний результат:

  Якщо\(y = a\sin(bt + c) + d\) або\(y = a\cos(bt + c) + d\), то

• Амплітуда синусоїди дорівнює\(|a|\).
• Період синусоїди становить\(\dfrac{2\pi}{b}\)
• Фазовий зсув синусоїди становить\(-\dfrac{c}{b}\)
• Вертикальний зсув синусоїди є\(d\).

Вправа\(\PageIndex{3}\)

• Визначте амплітуду, період, зсув фаз та вертикальний зсув для кожної з наступних синусоїд. Потім використовуйте цю інформацію, щоб графікувати один повний період синусоїди та вказати координати високої точки, низької точки та точки, де синусоїда перетинає центральну лінію.

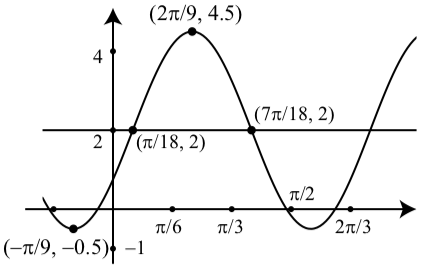
  (а)\(y = -2.5\cos(3x + \dfrac{\pi}{3}) + 2\)

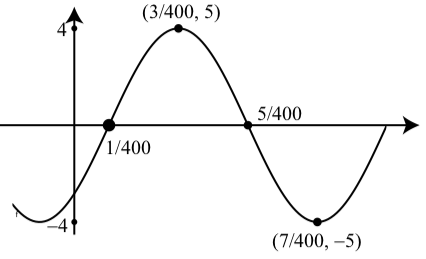
  (б)\(y = 4\sin(100\pi x - \dfrac{\pi}{4})\)

• Ми визначили дві синусоїдальні моделі за кількістю годин денного світла в Единбурзі, Шотландія, показані в таблиці 2.2. Це були

  \[y = 5.22\sin(\dfrac{\pi}{6}(t - 3.7)) + 12.28\]\[y = 5.153\sin(0.511t - 1.829) + 12.174\]

• Друге рівняння було визначено за допомогою функції синусоїдної регресії на графічній утиліті. Порівняйте амплітуди, періоди, фазові зрушення та вертикальні зсуви цих двох синусоїдальних функцій.

Відповідь

1. (а) Амплітуда становить\(2.5\).

Період є\(\dfrac{2\pi}{3}\).

Зсув фаз є\(-\dfrac{\pi}{9}\). Вертикальний зсув є\(2\).

(б) Амплітуда дорівнює\(4\).

Період - це\(\dfrac{1}{50}\)

Зсув фаз є\(\dfrac{1}{400}\).

Вертикальний зсув є\(0\).

перше рівняння		друге рівняння
\(5.22\)	амплітуда	\(5.153\)
\(12\)	період	\(12.30\)
\(3.7\)	фазовий зсув	\(3.58\)
\(12.28\)	вертикальний зсув	\(12.174\)

Доповнення - синусоїдна регресія за допомогою Geogebra

Перш ніж давати письмові інструкції щодо створення рівняння синусоїдної регресії в Geogebra, слід зазначити, що на YouTube є список відтворення Geogebra State University Math Channel. Веб-адреса http://gvsu.edu/s/QA

Відеоекрани, які зараз представляють найбільший інтерес:

• Геогебра - базова графіка
• Geogebra - копіювання графічного перегляду
• Geogebra - точки побудови
• Гегебра - синусоїдальна регресія

Щоб проілюструвати процедуру рівняння синусоїдної регресії за допомогою Geogebra, ми будемо використовувати дані в таблиці 2.2 на сторінці 115.

Крок 1. Встановіть вікно перегляду, відповідне тим даним, які будуть використовуватися.

Крок 2. Введіть точки даних. Є три способи зробити це.

• Мабуть, найефективнішим способом введення точок є використання перегляду електронних таблиць. Для цього натисніть на меню «Перегляд» і виберіть «Електронна таблиця». Справа відкриється невелика електронна таблиця. Хоча ви можете використовувати будь-які набори рядків і стовпців, простим способом є використання комірок A1 і B1 для першої точки даних, осередків A2 і B2 для другої точки даних і так далі. Отже, перші кілька рядків у електронній таблиці будуть такими:

  	\(A\)	\(B\)
  1	\ (A\) ">1	\ (B\) ">7,08
  2	\ (A\) ">2	\ (B\) ">8.6
  3	\ (A\) ">3	\ (B\) ">10.73

Після введення всіх даних для побудови точок виберіть рядки та стовпці в електронній таблиці, які містять дані, потім натисніть на маленьку стрілку вниз внизу праворуч від кнопки з міткою\({1, 2}\) та виберіть «Створити список точок». З'явиться невеликий спливаючий екран, в якому списку точок можна дати назву. Типовою назвою є «list'», але її можна змінити за бажанням. Тепер натисніть на кнопку Створити в нижній правій частині спливаючого екрану. Якщо встановлено належне вікно перегляду, точки повинні відображатися у графічному перегляді. Нарешті, закрийте перегляд електронних таблиць.

• Введіть кожну точку окремо як пару замовлень. Наприклад, для першого пункту в таблиці 2.2 ми б ввели\((1, 7.08)\). В цьому випадку кожній точці буде присвоєно таке ім'я\(A, B, C\), як і т.д.
• Введіть усі пункти у списку. Наприклад (для меншого набору точок) ми могли б ввести щось на кшталт\ [pts = {(-3, 3), (-2, -1), (0, 1), (1, 3), (3, 0)}\) Зверніть увагу, що список впорядкованих пар повинен бути укладений у фігурні дужки.

Крок 3. Скористайтеся командою FitSin. Як це буде використано, залежить від того, який параметр використовувався для введення та побудови точок даних.

• Якщо було створено список точок (наприклад, один з іменем list1), просто введіть\[f(x) = FitSin[list1]\] Все, що потрібно, це назва списку всередині дужок.
• Якщо були введені окремі точки даних, включіть імена всіх точок всередині дужок і відокремте їх комами. Скорочена версія:\ [f (x) = fitsIn [A, B, C]\) Рівняння синусоїдної регресії тепер буде показано у вигляді алгебри і буде відображено у графічному перегляді.

Крок 4. Виберіть параметр округлення, який буде використовуватися. (Цей крок можна виконати в будь-який час.) Для цього натисніть на меню Параметри і виберіть Округлення.

Резюме

У цьому розділі ми вивчили наступні важливі поняття та ідеї:

• Частота синусоїдальної функції - це кількість періодів (або циклів) в одиницю часу. \[frequency = \dfrac{1}{period}\]
• Математична модель - це функція, яка описує якесь явище. Для об'єктів, які проявляють періодичну поведінку, в якості моделі може використовуватися синусоїдальна функція, оскільки ці функції є періодичними.

Щоб визначити синусоїдальну функцію, яка моделює періодичні явища, нам потрібно визначити амплітуду, період і вертикальний зсув для періодичних явищ. Крім того, нам потрібно визначити, чи використовувати функцію косинуса або функцію синуса і результуючий фазовий зсув. Можна визначити рівняння синусоїдальної регресії, яке є математичним «найкращим чином» для даних періодичних явищ.