12.3: Геометричні формули

Таблиця С1 - 2 Розміри

Ім'я	Форма	Формули
Прямокутник		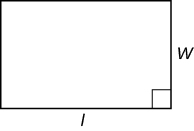Периметр: P =$2l + 2w$ Площа: A =$lw$
Квадрат		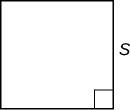Периметр: P = 4s Площа: A = s ^2
Трикутник		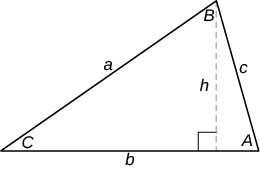Периметр: P = a + b + c Площа: A =$\dfrac{1}{2}$ bh Сума кутів: A + B + C = 180°
Правий трикутник		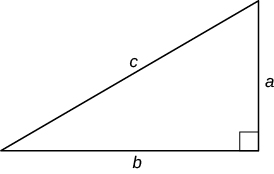Теорема Піфагора: a ^2 + b ^2 = c ^2 Площа: A =$\dfrac{1}{2}$ ab
Коло		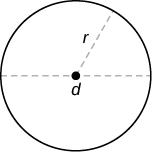Окружність: C = 2$\pi$ r або C =$\pi$ d Площа: A =$\pi$ r ^2
Паралелограм		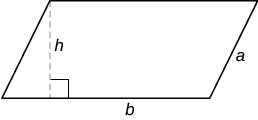Периметр: P = 2a + 2b Площа: A = bh
Трапеція		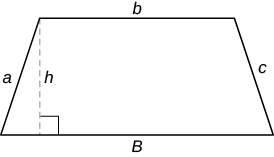Периметр: P = a + b + c + B Площа: A =$\dfrac{1}{2}$ (B + b) h

Таблиця С2 - 3 Розміри

Ім'я	Форма	Формули
прямокутний суцільний		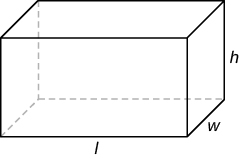Обсяг: V =$lwh$ Площа поверхні: SA =$2lw + 2wh + 2hl$
Куб		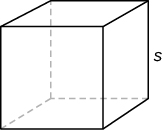Обсяг: V = s ^3 Площа поверхні: SA = 6s ^2
Конус		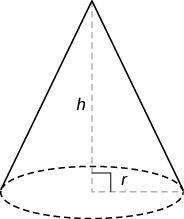Обсяг: V =$\dfrac{1}{3} \pi r^{2} h$ Площа поверхні: SA =$\pi r^{2} + \pi r \sqrt{h^{2} + r^{2}}$
Сфера		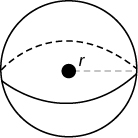Обсяг: V =$\dfrac{4}{3} \pi r^{3}$ Площа поверхні: SA =$4 \pi r^{2}$
Правий круговий циліндр		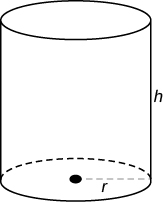Обсяг: V =$\pi r^{2} h$ Площа поверхні: SA =$2 \pi r^{2} + 2 \pi rh$

Дописувачі та авторства

• Template:ContribOpenStaxPreAlgebra