4.1: Візуалізація дробів (частина 1)
- Page ID
- 57805
- Зрозумійте значення дробів
- Модель неправильних дробів та мішаних чисел
- Перетворення між неправильними дробами та мішаними числами
- Модель еквівалентних дробів
- Знайти еквівалентні дроби
- Знайдіть дроби та мішані числа на числовому рядку
- Порядок дробів та мішаних чисел
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Спростити:\(5 • 2 + 1\). Якщо ви пропустили цю проблему, перегляньте приклад 2.1.8.
- Заповніть бланк за допомогою\(<\) або\(>\):\(−2\) __\(−5\). Якщо ви пропустили цю проблему, перегляньте приклад 3.1.2.
Зрозумійте значення дробів
Енді і Боббі люблять піцу. У ніч на понеділок вони поділяють піцу порівну. Скільки піци отримує кожен з них? Ви думаєте, що кожен хлопчик отримує половину піци? Це вірно. Є одна ціла піца, рівномірно розділена на дві частини, тому кожен хлопчик отримує одну з двох рівних частин. У математиці ми пишемо,\(\dfrac{1}{2}\) щоб означати одну з двох частин.
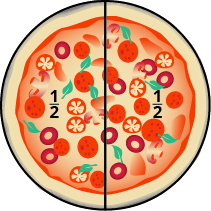
Малюнок\(\PageIndex{1}\)
У вівторок Енді і Боббі діляться піцою зі своїми батьками, Фредом і Крісті, при цьому кожна людина отримує рівну кількість всієї піци. Скільки піци отримує кожна людина? Є одна ціла піца, розділена рівномірно на чотири рівні частини. Кожна людина має одну з чотирьох рівних частин, тому кожна має\(\dfrac{1}{4}\) піцу.

Малюнок\(\PageIndex{2}\)
У середу сім'я запрошує друзів на вечерю з піцою. Є загальна кількість\(12\) людей. Якщо вони поділяють піцу порівну, кожна людина\(\dfrac{1}{12}\) отримає піцу.
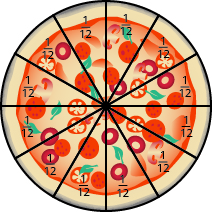
Малюнок\(\PageIndex{3}\)
Записується дріб\(\dfrac{a}{b}\), де\(a\) і\(b\) - цілі числа і\(b ≠ 0\). У дробі,\(a\) називається чисельником і\(b\) називається знаменником.
Дріб - це спосіб представлення частин цілого. Знаменник\(b\) являє собою кількість рівних частин, на які було поділено ціле, а чисельник\(a\) - скільки частин включено. Знаменник не може дорівнювати нулю\(b\), оскільки ділення на нуль не визначено.
На\(\PageIndex{4}\) малюнку коло розділено на три частини однакового розміру. Кожна\(\dfrac{1}{3}\) частина являє собою коло. Цей тип моделі називається дробовим кругом. Інші форми, такі як прямокутники, також можуть бути використані для моделювання дробів.
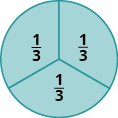
Малюнок\(\PageIndex{4}\)
Що\(\dfrac{2}{3}\) являє собою дріб? Дріб\(\dfrac{2}{3}\) означає дві з трьох рівних частин.
Малюнок\(\PageIndex{5}\)
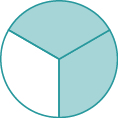
Назвіть частку фігури, яка затінена в кожній з фігур.
Рішення
Нам потрібно задати два питання. По-перше, скільки рівних частин? Це і буде знаменник. По-друге, з цих рівних частин, скільки затінюють? Це і буде чисельник.
| Скільки рівних частин там? | Є вісім рівних частин. |
| Скільки затінюються? | П'ять частин розтушовують. |
П'ять з восьми частин затінюються. Тому частка кола, яка затінюється, є\(\dfrac{5}{8}\).
| Скільки рівних частин там? | Є дев'ять рівних частин. |
| Скільки затінюються? | Дві частини розтушовують. |
Дві з дев'яти частин затінюються. Тому частка квадрата, яка затінюється, є\(\dfrac{2}{9}\).
Назвіть частку фігури, яка затінена на кожному малюнку:
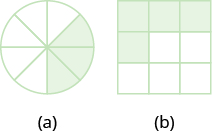
- Відповідь на
-
\(\dfrac{3}{8}\)
- Відповідь б
-
\(\dfrac{4}{9}\)
Назвіть частку фігури, яка затінена на кожному малюнку:
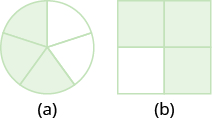
- Відповідь на
-
\(\dfrac{3}{5}\)
- Відповідь б
-
\(\dfrac{3}{4}\)
\(\dfrac{3}{4}\)Відтінок кола.

Рішення
Знаменник є\(4\), тому ділимо коло на чотири рівні частини (а). Чисельник є\(3\), тому ми затінюємо три з чотирьох частин (б).
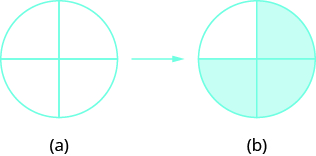
\(\dfrac{3}{4}\)кола розтушовується.
\(\dfrac{6}{8}\)Відтінок кола.
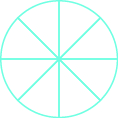
- Відповідь
-
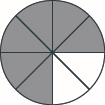
\(\dfrac{2}{5}\)Відтінок прямокутника.

- Відповідь
-

У\(\PageIndex{1}\) Example та\(\PageIndex{2}\) Example ми використовували кола та прямокутники для моделювання дробів. Дроби також можуть бути змодельовані як маніпулятори, які називаються фракційними плитками, як показано на малюнку\(\PageIndex{6}\). Тут ціле моделюється як одна довга, нерозділена прямокутна плитка. Під ним знаходяться плитки однакової довжини, розділені на різну кількість однакових за розміром частин.
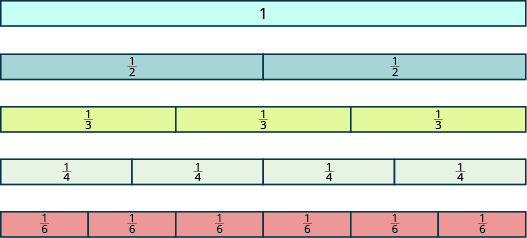
Малюнок\(\PageIndex{6}\)
Ми будемо використовувати фракційні плитки, щоб виявити деякі основні факти про фракції. Зверніться до Рисунок\(\PageIndex{6}\), щоб відповісти на наступні питання:
| Скільки\(\dfrac{1}{2}\) плитки потрібно, щоб зробити одну цілу плитку? | Потрібно дві половинки, щоб зробити ціле, тому дві з двох дорівнює\(\dfrac{2}{2}\) = 1. |
| Скільки\(\dfrac{1}{3}\) плитки потрібно, щоб зробити одну цілу плитку? | Це займає три третини, тому три з трьох\(\dfrac{3}{3}\) = 1. |
| Скільки\(\dfrac{1}{4}\) плитки потрібно, щоб зробити одну цілу плитку? | Це займає чотири четверті, тому чотири з чотирьох\(\dfrac{4}{4}\) = 1. |
| Скільки\(\dfrac{1}{5}\) плитки потрібно, щоб зробити одну цілу плитку? | Це займає шість шостих, тому шість з шести\(\dfrac{6}{6}\) = 1. |
| Що робити, якщо цілі були розділені на 24 рівні частини? (Ми не показали фракційні плитки, щоб представити це, але спробуйте візуалізувати це у вашій свідомості.) Скільки\(\dfrac{1}{24}\) плитки потрібно, щоб зробити одну цілу плитку? | Це займає 24 двадцять четвертих, так\(\dfrac{24}{24}\) = 1. |
Знадобиться\(24\) двадцять четвертих, значить\(\dfrac{24}{24} = 1\). Це призводить нас до Власності Одного.
Будь-яке число, крім нуля, розділене саме по собі, дорівнює одиниці.
\[\dfrac{a}{a} = 1 \qquad \qquad (a \neq 0)\]
Використовуйте дробові кола, щоб зробити цілі, використовуючи такі шматки:
- \(4\)четвертих
- \(5\)п'ятих
- \(6\)шістдесятих
Рішення
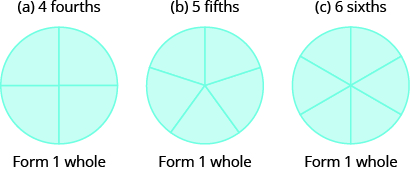
Використовуйте дробові кола, щоб зробити цілі з наступними шматочками:\(3\) третини.
- Відповідь
-
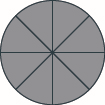
Використовуйте дробові кола, щоб зробити цілі з наступними шматочками:\(8\) восьмі.
- Відповідь
-
Що робити, якщо у нас є більше фракцій, ніж нам потрібно для\(1\) цілих? Ми розглянемо це в наступному прикладі.
Використовуйте дробові кола, щоб зробити цілі, використовуючи такі шматки:
- \(3\)половинки
- \(8\)п'ятих
- \(7\)третин
Рішення
- \(3\)половинки зробити\(1\) цілими з\(1\) половиною, що залишилася.
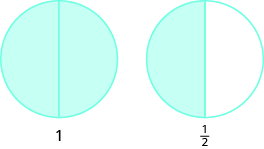
- \(8\)п'яті зробити\(1\) цілими з\(3\) п'ятими залишилися.
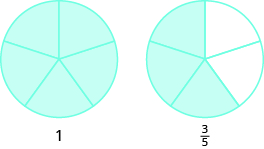
- \(7\)третини зробіть\(2\) цілі з\(1\) третім залишився.
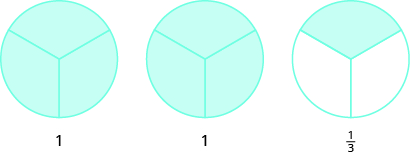
Використовуйте дробові кола, щоб зробити цілі з наступними шматочками:\(5\) третини.
- Відповідь
-
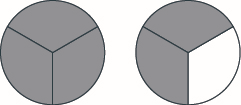
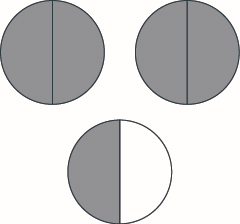
Використовуйте дробові кола, щоб зробити цілі з наступних шматочків:\(5\) половинки.
- Відповідь
-
Модель неправильних дробів та мішаних чисел
У прикладі\(\PageIndex{4b}\) у вас було вісім рівних п'ятих штук. Ви використали п'ять з них, щоб зробити одне ціле, і у вас залишилося три п'ятих. Давайте використаємо позначення дробу, щоб показати, що сталося. У вас було вісім штук, кожна з них одна п'ята\(\dfrac{1}{5}\), тож у вас було вісім п'ятих, які ми можемо написати як\(\dfrac{8}{5}\). Дріб\(\dfrac{8}{5}\) - це одне ціле\(1\), плюс три п'ятих, або\(\dfrac{3}{5}\)\(1 \dfrac{3}{5}\), що читається як одна, так і три-п'ята.
Число\(1 \dfrac{3}{5}\) називається мішаним числом. Мішане число складається з цілого числа і дробу.
Мішане число складається з цілого числа\(a\) і дробу\(\dfrac{b}{c}\) де\(c ≠ 0\). Вона пишеться наступним чином.
\[a \dfrac{b}{c} \qquad \qquad c \neq 0\]
Дроби, такі як\(\dfrac{5}{4}\),\(\dfrac{3}{2}\),\(\dfrac{5}{5}\), і\(\dfrac{7}{3}\) називаються неправильними дробами. У неправильному дробі чисельник більше або дорівнює знаменнику, тому його значення більше або дорівнює одиниці. Коли дріб має чисельник, який менше знаменника, він називається правильним дробом, а його значення менше одиниці. Дроби, такі як\(\dfrac{1}{2}\)\(\dfrac{3}{7}\), і\(\dfrac{11}{18}\) є правильними дробами.
Фракція\(\dfrac{a}{b}\) є правильною фракцією if\(a < b\) і неправильною фракцією if\(a ≥ b\).
Назвіть неправильний дріб, змодельований. Потім запишіть неправильний дріб як змішане число.
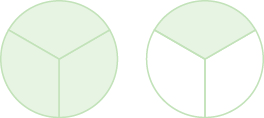
Рішення
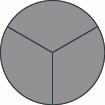
Кожне коло ділиться на три частини, тому кожен шматочок\(\dfrac{1}{3}\) складається з кола. Є чотири шматки затінені, тому є чотири третини або\(\dfrac{4}{3}\). На малюнку видно, що у нас також є одне ціле коло і одна третина, яка є\(1 \dfrac{1}{3}\). Отже,\(\dfrac{4}{3} = 1 \dfrac{1}{3}\).
Назвіть неправильний дріб. Потім запишіть його як змішане число.
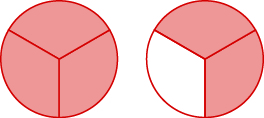
- Відповідь
-
\(\dfrac{5}{3}=1\dfrac{2}{3}\)
Назвіть неправильний дріб. Потім запишіть його як змішане число.
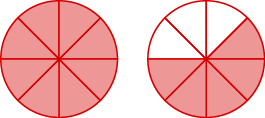
- Відповідь
-
\(\dfrac{13}{8}=1\dfrac{5}{8}\)
Намалюйте фігуру до моделі\(\dfrac{11}{8}\).
Рішення
Знаменником неправильного дробу є\(8\). Намалюйте коло, розділене на вісім частин, і розтушуйте всі їх. Це піклується про вісім восьмих, але у нас є\(11\) восьмі. Треба затінювати три з восьми частин іншого кола.
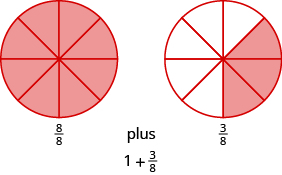
Отже,\(\dfrac{11}{8} = 1 \dfrac{3}{8}\).
Намалюйте фігуру до моделі\(\dfrac{7}{6}\).
- Відповідь
-
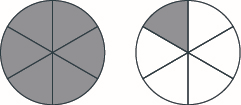
Намалюйте фігуру до моделі\(\dfrac{6}{5}\).
- Відповідь
-
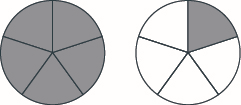
Використовуйте модель, щоб переписати неправильний дріб\(\dfrac{11}{6}\) як змішане число.
Рішення
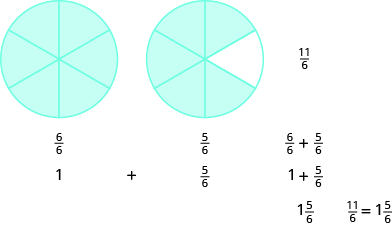
Починаємо з\(11\) шостих\(\left(\dfrac{11}{6}\right)\). Ми знаємо, що шість шостих складають одне ціле.
\[\dfrac{6}{6} = 1 \nonumber \]
Це залишає нам ще п'ять шістдесятих, тобто\(\dfrac{5}{6}\) (11 шостих мінус 6 шостих - це 5 шостих). Отже,\(\dfrac{11}{6} = 1 \dfrac{5}{6}\).
Використовуйте модель, щоб переписати неправильний дріб як змішане число:\(\dfrac{9}{7}\).
- Відповідь
-
\(1\dfrac{2}{7}\)
Використовуйте модель, щоб переписати неправильний дріб як змішане число:\(\dfrac{7}{4}\).
- Відповідь
-
\(1\dfrac{3}{4}\)
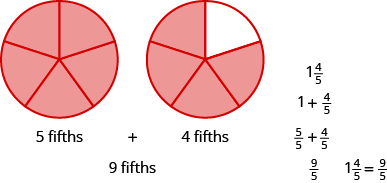
Використовуйте модель, щоб переписати мішане число\(1 \dfrac{4}{5}\) як неправильний дріб.
Рішення
Змішане число\(1 \dfrac{4}{5}\) означає одне ціле плюс чотири п'ятих. Знаменник є\(5\), тому ціле є\(\dfrac{5}{5}\). Разом п'ять п'ятих і чотири п'ятих дорівнює дев'яти п'ятих. Отже,\(1 \dfrac{4}{5} = \dfrac{9}{5}\).
Використовуйте модель, щоб переписати мішане число як неправильний дріб:\(1 \dfrac{3}{8}\).
- Відповідь
-
\(\dfrac{11}{8}\)
Використовуйте модель, щоб переписати мішане число як неправильний дріб:\(1 \dfrac{5}{6}\).
- Відповідь
-
\(\dfrac{11}{6}\)
Перетворення між неправильними дроби та мішаними числами
У прикладі\(\PageIndex{7}\) ми перетворили неправильний дріб\(\dfrac{11}{6}\) у мішане число,\(1 \dfrac{5}{6}\) використовуючи кола дробів. Ми зробили це, групуючи шість шостих разом, щоб скласти ціле; потім ми подивилися, скільки\(11\) частин залишилося. Ми побачили, що\(\dfrac{11}{6}\) склала одну цілу групу з шести шостих плюс п'ять ще шостих, показуючи це\(\dfrac{11}{6} = \dfrac{15}{6}\).
Вираз поділу\(\dfrac{11}{6}\) (який також може бути записаний як\(6 \overline{\smash{)}11}\)) говорить нам, щоб знайти, скільки груп\(6\) знаходяться в\(11\). Щоб перетворити неправильний дріб в мішане число без кіл дробу, ділимо.
\(\dfrac{11}{6}\)Перетворити на мішане число.
Рішення
| Розділіть знаменник на чисельник. | Запам'ятайте\(\dfrac{11}{6}\) кошти 11 ÷ 6. |
| Визначте частку, залишок і дільник. | 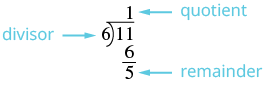 |
| Запишіть мішане число як\(quotient \dfrac{remainder}{divisor}\). | \(1 \dfrac{5}{6}\) |
Отже,\(\dfrac{11}{6} = 1 \dfrac{5}{6}\).
Перетворення неправильного дробу в мішане число:\(\dfrac{13}{7}\).
- Відповідь
-
\(1\dfrac{6}{7}\)
Перетворення неправильного дробу в мішане число:\(\dfrac{14}{9}\).
- Відповідь
-
\(1\dfrac{5}{9}\)
Крок 1. Розділіть знаменник на чисельник.
Крок 2. Визначте частку, залишок і дільник.
Крок 3. Запишіть мішане число як\(quotient \dfrac{remainder}{divisor}\).
Перетворення неправильного дробу\(\dfrac{33}{8}\) в мішане число.
Рішення
| Розділіть знаменник на чисельник. | Пам'ятайте,\(\dfrac{33}{8}\) значить\(8 \overline{\smash{)}33}\). |
| Визначте частку, залишок і дільник. | 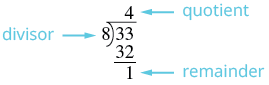 |
| Запишіть мішане число як\(quotient \dfrac{remainder}{divisor}\). | \(4 \dfrac{1}{8}\) |
Отже,\(\dfrac{33}{8} = 4 \dfrac{1}{8}\).
Перетворення неправильного дробу в мішане число:\(\dfrac{23}{7}\).
- Відповідь
-
\(3\dfrac{2}{7}\)
Перетворення неправильного дробу в мішане число:\(\dfrac{48}{11}\).
- Відповідь
-
\(4\dfrac{4}{11}\)
У прикладі\(\PageIndex{8}\) ми змінилися\(1 \dfrac{4}{5}\) на неправильний дріб, спочатку побачивши, що ціле - це набір з п'яти п'ятих. Таким чином, у нас було п'ять п'ятих і ще чотири п'ятих.
\[\dfrac{5}{5} + \dfrac{4}{5} = \dfrac{9}{5} \nonumber \]
Звідки взялася дев'ятка? Є дев'ять п'ятих - одне ціле (п'ять п'ятих) плюс чотири п'ятих. Давайте використаємо цю ідею, щоб побачити, як перетворити мішане число на неправильний дріб.
Перетворіть мішане число\(4 \dfrac{2}{3}\) на неправильний дріб.
| Помножте все число на знаменник. | \(4 \dfrac{2}{3}\) |
| Ціле число - 4, а знаменник - 3. | 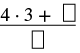 |
| Спростити. | 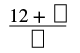 |
| Додайте чисельник до виробу. | |
| Чисельник мішаного числа дорівнює 2. | 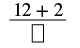 |
| Спростити. | 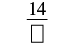 |
| Напишіть остаточну суму над початковим знаменником. | |
| Знаменник - 3. | \(\dfrac{14}{3}\) |
Перетворити мішане число на неправильний дріб:\(3 \dfrac{5}{7}\).
- Відповідь
-
\(\dfrac{26}{7}\)
Перетворити мішане число на неправильний дріб:\(2 \dfrac{7}{8}\).
- Відповідь
-
\(\dfrac{23}{8}\)
Крок 1. Помножте все число на знаменник.
Крок 2. Додайте чисельник до товару, знайденого на кроці 1.
Крок 3. Напишіть остаточну суму над початковим знаменником.
Перетворіть мішане число\(10 \dfrac{2}{7}\) на неправильний дріб.
| Помножте все число на знаменник. | \(10 \dfrac{2}{7}\) |
| Ціле число - 10, а знаменник - 7. | 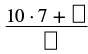 |
| Спростити. | 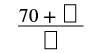 |
| Додайте чисельник до виробу. | |
| Чисельник мішаного числа дорівнює 2. | 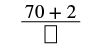 |
| Спростити. | 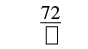 |
| Напишіть остаточну суму над початковим знаменником. | |
| Знаменник - 7. | \(\dfrac{72}{7}\) |
Перетворити мішане число на неправильний дріб:\(4 \dfrac{6}{11}\).
- Відповідь
-
\(\dfrac{50}{11}\)
Перетворити мішане число на неправильний дріб:\(11 \dfrac{1}{3}\).
- Відповідь
-
\(\dfrac{34}{3}\)