Skip to main content
LibreTexts - Ukrayinska

4.2: Візуалізація дробів (частина 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    57845

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Модель еквівалентних дробів

    Давайте знову подумаємо про Енді та Боббі та їх улюблену їжу. Якщо Енді\(\dfrac{1}{2}\) їсть піцу, а Боббі\(\dfrac{2}{4}\) їсть піцу, вони з'їли таку ж кількість піци? Іншими словами, робить\(\dfrac{1}{2} = \dfrac{2}{4}\)? Ми можемо використовувати фракційні плитки, щоб з'ясувати, чи з'їли Енді та Боббі еквівалентні частини піци.

    Визначення: Еквівалентні дроби

    Еквівалентні дроби - це дроби, які мають однакове значення.

    Фракційні плитки служать корисною моделлю еквівалентних дробів. Ви можете використовувати дробові плитки для виконання наступних дій. Або ви можете зробити копію малюнка 4.3 і розширити її, щоб включити восьмі, десяті та дванадцяті.

    Почніть з\(\dfrac{1}{2}\) плитки. Скільки четвертих дорівнює одній половині? Скільки з\(\dfrac{1}{4}\) плиток рівно покривають\(\dfrac{1}{2}\) плитку?

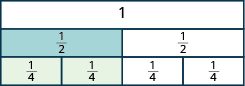
    Показаний один довгий, нерозділений прямокутник. Під ним знаходиться прямокутник, розділений вертикально на дві частини, кожна з яких позначена як одна половина. Нижче знаходиться прямокутник, розділений вертикально на чотири частини, кожна з яких позначена як одна четверта.

    Малюнок\(\PageIndex{7}\)

    Так як дві\(\dfrac{1}{4}\) плитки покривають\(\dfrac{1}{2}\) плитку, ми бачимо, що\(\dfrac{2}{4}\) таке ж\(\dfrac{1}{2}\), як, або\(\dfrac{2}{4} = \dfrac{1}{2}\).

    Скільки з\(\dfrac{1}{6}\) плитки покривають\(\dfrac{1}{2}\) плитку?

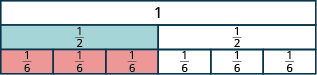
    Показаний один довгий, нерозділений прямокутник. Під ним знаходиться прямокутник, розділений вертикально на дві частини, кожна з яких позначена як одна половина. Нижче знаходиться прямокутник, розділений вертикально на шість частин, кожна з яких позначена як одна шоста.

    Малюнок\(\PageIndex{8}\)

    Так як три\(\dfrac{1}{6}\) плитки покривають\(\dfrac{1}{2}\) плитку, ми бачимо, що\(\dfrac{3}{6}\) це те ж саме, що і\(\dfrac{1}{2}\). Отже,\(\dfrac{3}{6} = \dfrac{1}{2}\). Дроби є еквівалентними дробами.

    Приклад\(\PageIndex{13}\): equivalent fractions

    Використовуйте фракційні плитки, щоб знайти еквівалентні дроби. Покажіть свій результат фігурою.

    1. Скільки восьмих дорівнює половині?
    2. Скільки десятих дорівнює одній половині?
    3. Скільки дванадцятих дорівнює одній половині?

    Рішення

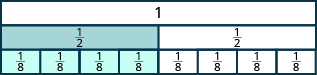
    1. Потрібно чотири\(\dfrac{1}{8}\) плитки, щоб рівно покрити\(\dfrac{1}{2}\) плитку, так\(\dfrac{4}{8} = \dfrac{1}{2}\).

    Показаний один довгий, нерозділений прямокутник, позначений 1. Під ним розташований ідентичний прямокутник, розділений вертикально на дві частини, кожна з яких позначена 1 половинкою. Нижче знаходиться ідентичний прямокутник, розділений вертикально на вісім частин, кожна з яких позначена 1 восьмою.

    1. Потрібно п'ять\(\dfrac{1}{10}\) плиток, щоб рівно покрити\(\dfrac{1}{2}\) плитку, так\(\dfrac{5}{10} = \dfrac{1}{2}\).

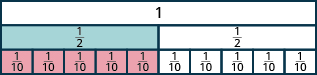
    Показаний один довгий, нерозділений прямокутник. Під ним знаходиться прямокутник, розділений вертикально на дві частини, кожна з яких позначена як одна половина. Нижче знаходиться прямокутник, розділений вертикально на десять частин, кожна з яких позначена як одна десята.

    1. Знадобиться шість\(\dfrac{1}{12}\) плиток, щоб рівно покрити\(\dfrac{1}{2}\) плитку, так\(\dfrac{6}{12} = \dfrac{1}{2}\).

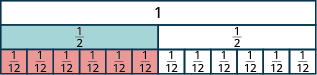
    Показаний один довгий, нерозділений прямокутник. Під ним знаходиться прямокутник, розділений вертикально на дві частини, кожна з яких позначена як одна половина. Нижче знаходиться прямокутник, розділений вертикально на дванадцять частин, кожна з яких позначена як одна дванадцята.

    Припустимо, у вас були позначені плитки\(\dfrac{1}{20}\). Скільки з них знадобилося б рівних\(\dfrac{1}{2}\)? Ви думаєте десять плиток? Якщо ви є, ви маєте рацію, тому що\(\dfrac{10}{20} = \dfrac{1}{2}\).

    Ми показали\(\dfrac{1}{2}, \dfrac{2}{4}, \dfrac{3}{6}, \dfrac{4}{8}, \dfrac{5}{10}, \dfrac{6}{12}\), що, і\(\dfrac{10}{20}\) всі еквівалентні дроби.

    Вправа\(\PageIndex{25}\)

    Використовуйте дробові плитки для пошуку еквівалентних дробів: Скільки восьмих дорівнює одній четвертій?

    Відповідь

    \(2\)

    Вправа\(\PageIndex{26}\)

    Використовуйте дробові плитки для пошуку еквівалентних дробів: Скільки дванадцятих дорівнює одній четвертій?

    Відповідь

    \(3\)

    Знайти еквівалентні дроби

    Ми використовували фракційні плитки, щоб показати, що існує багато фракцій, еквівалентних\(\dfrac{1}{2}\). Наприклад\(\dfrac{2}{4}, \dfrac{3}{6}\), і\(\dfrac{4}{8}\) всі еквівалентні\(\dfrac{1}{2}\). Коли ми вишикували фракційні плитки, знадобилося чотири\(\dfrac{1}{8}\) плитки, щоб зробити таку ж довжину, як\(\dfrac{1}{2}\) плитка. Це показало, що\(\dfrac{4}{8} = \dfrac{1}{2}\). Див\(\PageIndex{13}\). Приклад.

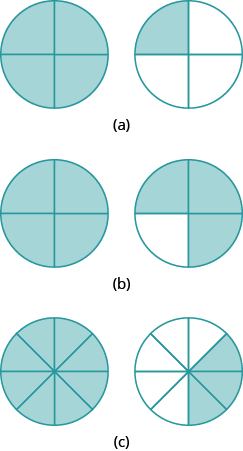
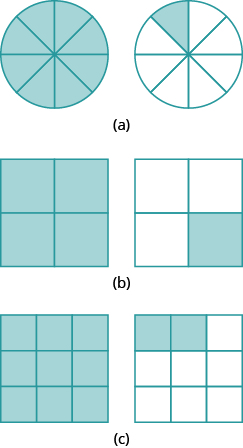
    Ми можемо показати це і з піцами. \(\PageIndex{9a}\)На малюнку зображена одиночна піца, розрізана на дві рівні частини з\(\dfrac{1}{2}\) розтушованими. \(\PageIndex{9b}\)На малюнку зображена друга піца такого ж розміру, розрізана на вісім частин з\(\dfrac{4}{8}\) розтушованими.

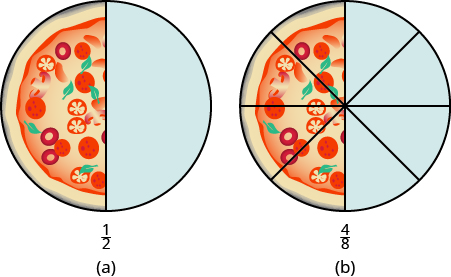
    Показані дві піци. Піца зліва ділиться на 2 рівні частини. 1 штука розтушовується. Піцу справа ділимо на 8 рівних частин. Розтушовуємо 4 штуки.

    Малюнок\(\PageIndex{9}\)

    Це ще один спосіб показати,\(\dfrac{1}{2}\) що еквівалентно\(\dfrac{4}{8}\). Як ми можемо використовувати математику, щоб\(\dfrac{1}{2}\) змінитися\(frac{4}{8}\)? Як можна взяти піцу, розрізану на дві частини і розрізати її на вісім частин? Ви можете розрізати кожен з двох великих шматочків на чотири менші шматочки! Вся піца потім буде розрізана на вісім частин замість двох. Математично те, що ми описали, можна записати як:

    \[\dfrac{1 \cdot \textcolor{blue}{4}}{2 \cdot \textcolor{blue}{4}} = \dfrac{4}{8} \nonumber \]

    Ці моделі призводять до властивості еквівалентних дробів, яке стверджує, що якщо помножити чисельник і знаменник дробу на одне і те ж число, значення дробу не змінюється.

    Визначення: Властивість еквівалентних дробів

    Якщо\(a\),\(b\), і\(c\) є числами де\(b ≠ 0\) і\(c ≠ 0\), то

    \[\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c}\]

    При роботі з дробами часто доводиться висловлювати один і той же дріб в різних формах. Щоб знайти еквівалентні форми дробу, ми можемо використовувати властивість Equivalt Fractions. Для прикладу розглянемо дріб полуторний.

    \[\begin{split} \dfrac{1 \cdot \textcolor{blue}{3}}{2 \cdot \textcolor{blue}{3}} = \dfrac{3}{6} \; & so \; \dfrac{1}{2} = \dfrac{3}{6} \\ \dfrac{1 \cdot \textcolor{blue}{2}}{2 \cdot \textcolor{blue}{2}} = \dfrac{2}{4} \; & so \; \dfrac{1}{2} = \dfrac{2}{4} \\ \dfrac{1 \cdot \textcolor{blue}{10}}{2 \cdot \textcolor{blue}{10}} = \dfrac{10}{20} \; & so \; \dfrac{1}{2} = \dfrac{10}{20} \end{split} \nonumber \]

    Отже, ми говоримо, що\(\dfrac{1}{2}, \dfrac{2}{4}, \dfrac{3}{6}\), і\(\dfrac{10}{20}\) є еквівалентними дробами.

    Приклад\(\PageIndex{14}\): equivalent fractions

    Знайти три дроби, еквівалентні\(\dfrac{2}{5}\).

    Рішення

    Щоб знайти дріб, еквівалентний\(\dfrac{2}{5}\), множимо чисельник і знаменник на одне і те ж число (але не нуль). Давайте помножимо їх на\(2\),\(3\), і\(5\).

    \[\dfrac{2 \cdot \textcolor{blue}{2}}{5 \cdot \textcolor{blue}{2}} = \dfrac{4}{10} \qquad \dfrac{2 \cdot \textcolor{blue}{3}}{5 \cdot \textcolor{blue}{3}} = \dfrac{6}{15} \qquad \dfrac{2 \cdot \textcolor{blue}{5}}{5 \cdot \textcolor{blue}{5}} = \dfrac{10}{25} \nonumber \]

    Отже\(\dfrac{4}{10}, \dfrac{6}{15}\), і\(\dfrac{10}{25}\) еквівалентні\(\dfrac{2}{5}\).

    Вправа\(\PageIndex{27}\)

    Знайти три дроби, еквівалентні\(\dfrac{3}{5}\).

    Відповідь

    Правильні відповіді включають\(\dfrac{6}{10}, \dfrac{9}{15}\) і\(\dfrac{12}{20}\)

    Вправа\(\PageIndex{28}\)

    Знайти три дроби, еквівалентні\(\dfrac{4}{5}\).

    Відповідь

    Правильні відповіді включають\(\dfrac{8}{10}, \dfrac{12}{15}\) і\(\dfrac{16}{20}\)

    Приклад\(\PageIndex{15}\): equivalent fractions

    Знайдіть дріб зі знаменником 21, що еквівалентно\(\dfrac{2}{7}\).

    Рішення

    Щоб знайти еквівалентні дроби, помножимо чисельник і знаменник на одне і те ж число. В цьому випадку нам потрібно помножити знаменник на число, яке вийде\(21\).

    Оскільки ми можемо\(7\) помножити на\(21\),\(3\) щоб отримати, ми можемо знайти еквівалентний дріб, помноживши і чисельник, і знаменник на\(3\).

    \[\dfrac{2}{7} = \dfrac{2 \cdot \textcolor{blue}{3}}{7 \cdot \textcolor{blue}{3}} = \dfrac{6}{21} \nonumber \]

    Вправа\(\PageIndex{29}\)

    Знайдіть дріб із знаменником\(21\), який еквівалентний\(\dfrac{6}{7}\).

    Відповідь

    \(\dfrac{18}{21}\)

    Вправа\(\PageIndex{30}\)

    Знайдіть дріб із знаменником\(100\), який еквівалентний\(\dfrac{3}{10}\).

    Відповідь

    \(\dfrac{30}{100}\)

    Знайдіть дроби та мішані числа на числовому рядку

    Тепер ми готові до побудови дробів на числовому рядку. Це допоможе нам візуалізувати дроби і зрозуміти їх значення.

    Давайте знайдемо\(\dfrac{1}{5}, \dfrac{4}{5}, 3, 3 \dfrac{1}{3}, \dfrac{7}{4}, \dfrac{9}{2}, 5\), і\(\dfrac{8}{3}\) на цифровому рядку. Почнемо ми з цілих чисел\(3\) і\(5\) тому, що вони найлегші для побудови сюжету.

    Буде показано числовий рядок з цифрами 3, 4 і 5. Є червоні точки на 3 і в 5.

    Правильні перелічені дроби - це\(\dfrac{1}{5}\) і\(\dfrac{4}{5}\). Ми знаємо, що правильні дроби мають значення менше одиниці, тому\(\dfrac{1}{5}\) і\(\dfrac{1}{5}\) розташовані між цілими числами\(0\) і\(1\). Знаменники обидва\(5\), тому нам потрібно розділити відрізок числової лінії між\(0\) і\(1\) на п'ять рівних частин. Ми можемо зробити це, намалювавши чотири однаково розташовані позначки на числовій лінії, яку ми можемо потім позначити як\(\dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5}\), і\(\dfrac{4}{5}\). Тепер сюжетні точки на\(\dfrac{1}{5}\) і\(\dfrac{4}{5}\).

    Відображається числовий рядок. Він показує 0, 1 п'ятий, 2 п'ятих, 3 п'ятих, 4 п'ятих і 1. Є червоні точки на 1 п'ятій і в 4 п'ятих.

    Єдине змішане число для сюжету є\(3 \dfrac{1}{3}\). Між якими двома цілими числами\(3 \dfrac{1}{3}\)? Пам'ятайте, що мішане число - це ціле число плюс правильний дріб, так що\(3 \dfrac{1}{3} > 3\). Так як вона більше\(3\), але не ціла одиниця більше,\(3 \dfrac{1}{3}\) знаходиться між\(3\) і\(4\). Нам потрібно розділити частину числової лінії між\(3\) і\(4\) на три рівні частини (третини) і відкласти\(3 \dfrac{1}{3}\) на першій позначці.

    Числовий рядок відображається цілим числом від 0 до 5. Між 3 і 4, 3 і 1 третина і 3 і 2 третини маркуються. Є червона точка на 3 і 1 третина.

    Нарешті, подивіться на неправильні\(\dfrac{7}{4}, \dfrac{9}{2}\) дроби, і\(\dfrac{8}{3}\). Розташування цих точок буде простіше, якщо ви поміняєте кожну з них на змішане число.

    \[\dfrac{7}{4} = 1 \dfrac{3}{4}, \qquad \dfrac{9}{2} = 4 \dfrac{1}{2}, \qquad \dfrac{8}{3} = 2 \dfrac{2}{3} \nonumber \]

    Ось числова лінія з нанесеними всіма точками.

    Числовий рядок відображається цілими числами від 0 до 6. Між 0 і 1, 1 п'ята та 4 п'ята позначені та показані червоними крапками. Між 1 і 2, 7 четвертих позначені і показані червоною крапкою. Між 2 і 3, 8 третин позначені і показані червоною крапкою. Між 3 і 4, 3 і 1 третина позначені і показані червоною крапкою. Між 4 і 5 9 половинками позначені і показані червоною крапкою.

    Приклад\(\PageIndex{16}\): locate and label

    Знайдіть і позначте на цифровому рядку наступне:\(\dfrac{3}{4}, \dfrac{4}{3}, \dfrac{5}{3}, 4 \dfrac{1}{5}\), і\(\dfrac{7}{2}\).

    Рішення

    Почніть з визначення місця належного дробу\(\dfrac{3}{4}\). Вона знаходиться між\(0\) і\(1\). Для цього розділіть відстань між\(0\) і\(1\) на чотири рівні частини. Потім змову\(\dfrac{3}{4}\).

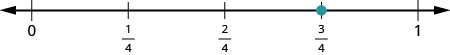
    Відображається числовий рядок. Він показує 0, 1 четверту, 2 четверті, 3 четверті та 1. Є червона точка на 3 четвертих.

    Далі знайдіть мішане число\(4 \dfrac{1}{5}\). Вона знаходиться між\(4\) і\(5\) на цифровому рядку. Розділіть числову лінію між\(4\) і\(5\) на п'ять рівних частин, а потім\(4 \dfrac{1}{5}\) нанесіть одну п'яту частину шляху між\(4\) і\(5\).

    Відображається числовий рядок. Він показує 4, 4 і 1 п'яту, 4 і 2 п'яті, 4 і 3 п'яті, 4 і 4 п'яті, і 5. Є червона точка на 4 і 1 п'ята.

    Тепер знайдіть неправильні\(\dfrac{4}{3}\) дроби і\(\dfrac{5}{3}\). Їх простіше побудувати, якщо спочатку перетворити їх на змішані числа.

    \[\dfrac{4}{3} = 1 \dfrac{1}{3}, \qquad \dfrac{5}{3} = 1 \dfrac{2}{3} \nonumber\]

    Розділіть відстань між\(1\) і\(2\) на третини.

    Відображається числовий рядок. Він показує 1, 1 і 1 третину, 1 і 2 третини, і 2. Нижче 1 написано 3 третини. Нижче 1 і 1 третина написано 4 третини. Нижче 1 і 2 третини написано 5 третин. Нижче 2 написано 6 третин. Є червоні точки на 1 і 1 третину і 1 і 2 третини.

    Далі давайте змову\(\dfrac{7}{2}\). Пишемо його як змішане число,\(\dfrac{7}{2} = 3 \dfrac{1}{2}\). Ділянка його між\(3\) і\(4\).

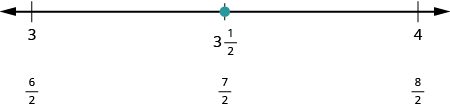
    Відображається числовий рядок. Він показує 3, 3 і 1 половину, і 4. Нижче 3 написано 6 половин. Нижче 3 і 1 половина написано 7 половин. Нижче 4 написано 8 половин. Є червона точка на 3 і 1 половині.

    У цифровому рядку відображаються всі числа, розташовані на числовому рядку.

    Відображається числовий рядок. Він показує цілі числа від 0 до 5. Між будь-якими 2 числами стоять 10 галочок. Між 0 і 1, між 7-м і 8-м відміткою, 3 четверті позначені і показані червоною крапкою. Між 1 і 2, 4 третини і 5 третин позначені і показані червоними крапками. Між 3 і 4 7 половинками позначені і показані червоною крапкою. Між 4 і 5, 4 і 1 п'ята позначена і показана червоною крапкою.

    Вправа\(\PageIndex{31}\)

    Знайдіть і позначте наступне на цифровому рядку:\(\dfrac{1}{3}, \dfrac{5}{4}, \dfrac{7}{4}, 2 \dfrac{3}{5}, \dfrac{9}{2}\).

    Відповідь

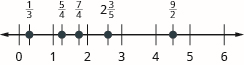
    Вправа 4.1.31.png

    Вправа\(\PageIndex{32}\)

    Знайдіть і позначте наступне на цифровому рядку:\(\dfrac{2}{3}, \dfrac{5}{2}, \dfrac{9}{4}, \dfrac{11}{4}, 3 \dfrac{2}{5}\).

    Відповідь

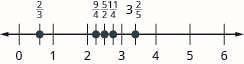
    Вправа 4.1.32.png

    У Вступі до цілих чисел ми визначили протилежне числу. Це число, яке однакова відстань від нуля на числовій лінії, але на протилежній стороні нуля. Ми побачили, наприклад, що\(7\) протилежне є\(−7\) і протилежне\(−\) 7 є\(7\).

    Відображається числовий рядок. Він показує числа від'ємні 7, 0 і 7. Є червоні точки при негативних 7 і 7. Простір між негативними 7 і 0 позначається як 7 одиниць. Простір між 0 і 7 позначено як 7 одиниць.

    Дроби теж мають протилежності. Протилежність\(\dfrac{3}{4}\) є\(− \dfrac{3}{4}\). Це така ж відстань від\(0\) на числовій лінії, але з протилежного боку\(0\).

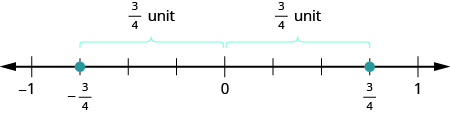
    Відображається числовий рядок. Він показує числа від'ємні 1, від'ємні 3 четверті, 0, 3 четверті та 1. З'являються червоні точки при негативних 3 четвертих і 3 четвертих. Простір між негативними 3 четвертами і 0 позначається як 3 четверті одиниці. Простір між 0 і 3 четвертими позначається як 3 чверті одиниці.

    Думаючи про негативні дроби як протилежні додатним дроби, ми можемо знайти їх на числовому рядку. Щоб знайти\(− \dfrac{15}{8}\) на цифровому рядку, спочатку подумайте, де\(\dfrac{15}{8}\) знаходиться. Це неправильний дріб, тому ми спочатку перетворюємо його в змішане число\(1 \dfrac{7}{8}\) і бачимо, що воно буде між\(1\) і\(2\) на числовому рядку. Таким чином, його протилежність\(− \dfrac{15}{8}\), буде між\(−1\) і\(−2\) на числовому рядку.

    Відображається числовий рядок. Він показує числа від'ємні 2, від'ємні 1, 0, 1 і 2. Між негативними 2 і негативними 1 від'ємні 1 і 7 восьмі позначені і позначені червоною крапкою. Відстань між від'ємними 1 і 7 восьмими і 0 позначається як 15 восьмих одиниць. Між 1 і 2, 1 і 7 восьмими позначені і позначені червоною крапкою. Відстань між 0 і 1 і 7 восьмими відзначається як 15 восьмих одиниць.

    Приклад\(\PageIndex{17}\): locate and label

    Знайдіть і позначте на цифровому рядку наступне:\(\dfrac{1}{4}, − \dfrac{1}{4}, 1 \dfrac{1}{3}, −1 \dfrac{1}{3}, \dfrac{5}{2}\), і\(− \dfrac{5}{2}\).

    Рішення

    Намалюйте числову лінію. Позначте\(0\) посередині, а потім відзначте кілька одиниць зліва і справа.

    Щоб розташувати\(\dfrac{1}{4}\), розділіть інтервал між\(0\) і\(1\) на чотири рівні частини. Кожна частина являє собою одну чверть відстані. Так змова\(\dfrac{1}{4}\) на першій позначці.

    Відображається числовий рядок. Він показує числа негативні 4, негативні 3, негативні 2, негативні 1, 0, 1, 2, 3 та 4. Між негативними 1 і 0 є 4 галочки. Є 4 галочки між 0 і 1. Перша галочка між 0 і 1 позначена як 1 четверта і позначена червоною крапкою.

    Щоб розташувати\(− \dfrac{1}{4}\), розділіть інтервал між\(0\) і\(−1\) на чотири рівні частини. Ділянка\(− \dfrac{1}{4}\) на першій позначці зліва від\(0\).

    Відображається числовий рядок. Він показує числа негативні 4, негативні 3, негативні 2, негативні 1, 0, 1, 2, 3 та 4. Між негативними 1 і 0 є 4 галочки. Є 4 галочки між 0 і 1. Перша галочка між 0 і 1 позначена як 1 четверта і позначена червоною крапкою. Перша галочка між 0 і від'ємною 1 позначається як негативна 1 четверта і позначена червоною крапкою.

    Так як\(1 \dfrac{1}{3}\) знаходиться між\(1\) і\(2\), розділіть інтервал між\(1\) і\(2\) на три рівні частини. Ділянка\(1 \dfrac{1}{3}\) на першій позначці праворуч від\(1\). Тоді\(−1 \dfrac{1}{3}\) так як протилежність\(1 \dfrac{1}{3}\) йому знаходиться між\(−1\) і\(−2\). Розділіть інтервал між\(−1\) і\(−2\) на три рівні частини. Ділянка\(−1 \dfrac{1}{3}\) на першій позначці зліва від\(−1\).

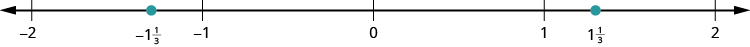
    Відображається числовий рядок. Позначені цілі числа від від'ємного 2 до 2. Між негативними 2 і негативними 1 від'ємні 1 і 1 третина позначені і позначені червоною крапкою. Між 1 і 2, 1 і 1 третина позначена і позначена червоною крапкою.

    Щоб знайти\(\dfrac{5}{2}\) і\(− \dfrac{5}{2}\), може бути корисно переписати їх як змішані числа\(2 \dfrac{1}{2}\) і\(−2 \dfrac{1}{2}\). Оскільки\(2 \dfrac{1}{2}\) знаходиться між\(2\) і\(3\), розділіть інтервал між\(2\) і\(3\) на дві рівні частини. Ділянка\(\dfrac{5}{2}\) на позначці. Потім, оскільки\(−2 \dfrac{1}{2}\) знаходиться між\(−2\) і\(−3\), розділіть інтервал між\(−2\) і на\(−3\) дві рівні частини. Ділянка\(− \dfrac{5}{2}\) на позначці.

    Відображається числовий рядок. Позначені цілі числа від від'ємного 4 до 4. Між негативними 3 і негативними 2 від'ємні 5 половин позначені і позначені червоною крапкою. Між 2 і 3, 5 половинками позначено і позначено червоною крапкою.

    Вправа\(\PageIndex{33}\)

    Знайдіть і позначте кожен із заданих дробів у числовому рядку:\(\dfrac{2}{3}, − \dfrac{2}{3}, 2 \dfrac{1}{4}, −2 \dfrac{1}{4}, \dfrac{3}{2}, − \dfrac{3}{2}\)

    Відповідь

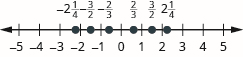
    Вправа 4.1.33.png

    Вправа\(\PageIndex{34}\)

    Знайдіть і позначте кожен із заданих дробів у числовому рядку:\(\dfrac{3}{4}, − \dfrac{3}{4}, 1 \dfrac{1}{2}, −1 \dfrac{1}{2}, \dfrac{7}{3}, − \dfrac{7}{3}\)

    Відповідь

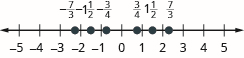
    Вправа 4.1.34.png

    Порядок дробів та мішаних чисел

    Ми можемо використовувати символи нерівності для впорядкування дробів. Пам'ятайте, що\(a\) це\(a > b\) означає, що знаходиться\(b\) праворуч від номера рядка. Коли ми рухаємося зліва направо по числовому рядку, значення збільшуються.

    Приклад\(\PageIndex{18}\): order

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):

    1. \(− \dfrac{2}{3}\)____\(−1\)
    2. \(−3 \dfrac{1}{2}\)____\(−3\)
    3. \(− \dfrac{3}{7}\)____\(− \dfrac{3}{8}\)
    4. \(−2\)____\(− \dfrac{16}{9}\)

    Рішення

    1. \(− \dfrac{2}{3} > −1\)

    Відображається числовий рядок. Позначені цілі числа від від'ємних 3 до 3. Негативний 1 позначається червоною крапкою. Між негативними 1 і 0 від'ємні 2 третини позначені і позначені червоною крапкою.

    1. \(−3 \dfrac{1}{2} < −3\)

    Відображається числовий рядок. Позначені цілі числа від від'ємного 4 до 4. Є червона крапка при негативному 3. Між негативними 4 і негативними 3 позначаються негативні 3 і одна половина і позначені червоною крапкою.

    1. \(− \dfrac{3}{7} < − \dfrac{3}{8}\)

    Відображається числовий рядок. Позначені числа від'ємні 3, від'ємні 2, від'ємні 1, 0, 1, 2 та 3. Між негативними 1 і 0 негативними 3 сьомими та негативними 3 восьмими позначені та позначені червоними крапками.

    1. \(−2 < − \dfrac{16}{9}\)

    Відображається числовий рядок. Позначені числа від'ємні 3, від'ємні 2, від'ємні 1, 0, 1, 2 та 3. Є червона крапка при негативному 2. Між негативними 2 і негативними 1 негативні 16 над 9 позначені і позначені червоною крапкою.

    Вправа\(\PageIndex{35}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):

    1. \(− \dfrac{1}{3}\)__\(−1\)
    2. \(−1 \dfrac{1}{2}\)__\(− 2\)
    3. \(− \dfrac{2}{3}\)__\(− \dfrac{1}{3}\)
    4. \(−3\)__\(− \dfrac{7}{3}\)
    Відповідь на

    \(>\)

    Відповідь б

    \(>\)

    Відповідь c

    \(<\)

    Відповідь d

    \(<\)

    Вправа\(\PageIndex{36}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):

    1. \(−3\)__\(− \dfrac{17}{5}\)
    2. \(−2 \dfrac{1}{4}\)__\(−2\)
    3. \(− \dfrac{3}{5}\)__\(− \dfrac{4}{5}\)
    4. \(−4\)__\(− \dfrac{10}{3}\)
    Відповідь на

    \(>\)

    Відповідь б

    \(<\)

    Відповідь c

    \(>\)

    Відповідь d

    \(<\)

    Ключові концепції

    • Власність одного
      • Будь-яке число, крім нуля, розділене саме по собі, дорівнює одиниці.
        \(\dfrac{a}{a}=1\), де\(a\neq 0\).
    • Змішані числа
      • Мішане число складається з цілого числа\(a\) і дробу\(\dfrac{b}{c}\) де\(c \neq 0\).
      • Вона пишеться наступним чином:\(a\dfrac{b}{c}\)\(c \neq 0\)
    • Правильні та неправильні дроби
      • Фракція\(\frac{a}{b}\) є правильною фракцією if\(a<b\) і неправильною фракцією if\(a \geq b\).
    • Перетворення неправильного дробу в мішане число.
      1. Розділіть знаменник на чисельник.
      2. Визначте частку, залишок і дільник.
      3. Запишіть мішане число як\(\dfrac{\text{remainder}}{\text{divisor}}\).
    • Перетворення мішаного числа на неправильний дріб.
      1. Помножте все число на знаменник.
      2. Додайте чисельник до товару, знайденого на кроці 1.
      3. Напишіть остаточну суму над початковим знаменником.
    • Властивість еквівалентних дробів
      • Якщо\(a\),\(b\) і\(c\) є числами де\(b \neq 0\)\(c \neq 0\), то\ (\ dfrac {a} {b} =\ dfrac {a\ cdot c} {b\ cdot c}\]).

    Глосарій

    еквівалентні дроби

    Еквівалентні дроби - це два або більше дробів, які мають однакове значення.

    фракція

    Записується дріб\(\dfrac{a}{b}\). в дріб,\(a\) є чисельником і\(b\) є знаменником. Дріб являє собою частини цілого. Знаменник\(b\) - це кількість рівних частин, на які було поділено ціле, а чисельник\(a\) вказує, скільки частин включено.

    змішане число

    Мішане число складається з цілого числа\(a\) і дробу\(\dfrac{b}{c}\) де\(c \neq 0\). Він пишеться як\(a\dfrac{b}{c}\), де\(c \neq 0\).

    правильні та неправильні дроби

    \(\dfrac{a}{b}\)Фракція належна, якщо\(a<b\) і неправильна, якщо\(a>b\).

    Практика робить досконалим

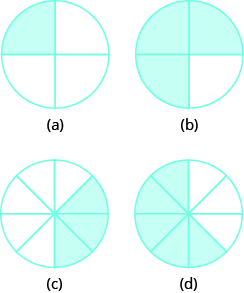
    1. У частині «а» коло ділиться на 4 рівні частини. 1 штука розтушовується. У частині «б» коло ділиться на 4 рівні частини. 3 штуки розтушовують. У частині «с» коло ділиться на 8 рівних частин. 3 штуки розтушовують. У частині «d» коло ділиться на 8 рівних частин. 5 штук розтушовують.
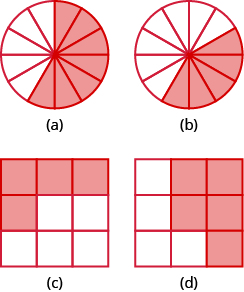
    2. У частині «а» коло ділиться на 12 рівних частин. Розтушовують 7 штук. У частині «б» коло ділиться на 12 рівних частин. Розтушовують 5 штук. У частині «с» квадрат ділиться на 9 рівних частин. 4 частини розтушовують. У частині «d» квадрат ділиться на 9 рівних частин. 5 штук розтушовують.

    У наступних вправах затінюйте частини кіл або квадратів для моделювання наступних дробів.

    1. \(\dfrac{1}{2}\)
    2. \(\dfrac{1}{3}\)
    3. \(\dfrac{3}{4}\)
    4. \(\dfrac{2}{5}\)
    5. \(\dfrac{5}{6}\)
    6. \(\dfrac{7}{8}\)
    7. \(\dfrac{5}{8}\)
    8. \(\dfrac{7}{10}\)

    У наступних вправах використовуйте дробові кола, щоб зробити цілі, якщо це можливо, з наступними шматочками.

    1. 3 третини
    2. 8 восьмих
    3. 7 шістдесятих
    4. 4 третини
    5. 7 п'ятих
    6. 7 четвертих

    У наступних вправах назвіть неправильні дроби. Потім запишіть кожен неправильний дріб як змішане число.

    1. У частині «а» показано два кола. Кожну розділити на 4 рівні частини. Коло зліва має всі 4 частини затінені. Коло праворуч має 1 шматок затінений. У частині «b» показано два кола. Кожну розділити на 4 рівні частини. Коло зліва має всі 4 частини затінені. Коло праворуч має 3 шматки затінені. У частині «c» показано два кола. Кожну розділити на 8 рівних частин. Коло зліва має всі 8 штук затінені. Коло праворуч має 3 шматки затінені.
    2. У частині «а» показано 2 кола. Кожну розділити на 8 рівних частин. Коло зліва має всі 8 штук затінені. Коло праворуч має 1 шматок затінений. У частині «b» показано два квадрата. Кожну розділити на 4 рівні частини. Квадрат зліва має всі 4 частини затінені. Коло праворуч має 1 шматок затінений. У частині «c» показано два квадрата. Кожну розділити на 9 рівних частин. Квадрат зліва має всі 9 штук затінені. Квадрат праворуч має 2 шматки затінені.
    3. У частині «а» показано 3 кола. Кожну розділити на 4 рівні частини. Перші два кола мають всі 4 штуки затінені. Третє коло має 3 штуки затінені. У частині «б» показано 3 кола. Кожну розділити на 8 рівних частин. Перші два кола мають всі 8 штук затінені. Третє коло має 3 штуки затінені.

    У наступних вправах намалюйте кола дробу для моделювання заданого дробу.

    1. \(\dfrac{3}{3}\)
    2. \(\dfrac{4}{4}\)
    3. \(\dfrac{7}{4}\)
    4. \(\dfrac{5}{3}\)
    5. \(\dfrac{11}{6}\)
    6. \(\dfrac{13}{8}\)
    7. \(\dfrac{10}{3}\)
    8. \(\dfrac{9}{4}\)

    У наступних вправах перепишіть неправильний дріб як змішане число.

    1. \(\dfrac{3}{2}\)
    2. \(\dfrac{5}{3}\)
    3. \(\dfrac{11}{4}\)
    4. \(\dfrac{13}{5}\)
    5. \(\dfrac{25}{6}\)
    6. \(\dfrac{28}{9}\)
    7. \(\dfrac{42}{13}\)
    8. \(\dfrac{47}{15}\)

    У наступних вправах перепишіть змішане число як неправильний дріб.

    1. \(1 \dfrac{2}{3}\)
    2. \(1 \dfrac{2}{5}\)
    3. \(2 \dfrac{1}{4}\)
    4. \(2 \dfrac{5}{6}\)
    5. \(2 \dfrac{7}{9}\)
    6. \(2 \dfrac{5}{7}\)
    7. \(3 \dfrac{4}{7}\)
    8. \(3 \dfrac{5}{9}\)

    У наступних вправах використовуйте дробові плитки або намалюйте фігуру, щоб знайти еквівалентні дроби.

    1. Скільки шістдесятих дорівнює третині?
    2. Скільки дванадцятих дорівнює третині?
    3. Скільки восьмих дорівнює трьом четвертам?
    4. Скільки дванадцятих дорівнює трьом четвертим?
    5. Скільки четвертих дорівнює трьом половинам?
    6. Скільки шістдесятих дорівнює трьом половинам?

    У наступних вправах знайдіть три дроби, еквівалентні заданому дробу. Покажіть свої роботи, використовуючи цифри або алгебру.

    1. \(\dfrac{1}{4}\)
    2. \(\dfrac{1}{3}\)
    3. \(\dfrac{3}{8}\)
    4. \(\dfrac{5}{6}\)
    5. \(\dfrac{2}{7}\)
    6. \(\dfrac{5}{9}\)

    У наступних вправах нанесіть цифри на числовій лінії.

    1. \(\dfrac{2}{3}, \dfrac{5}{4}, \dfrac{12}{5}\)
    2. \(\dfrac{1}{3}, \dfrac{7}{4}, \dfrac{13}{5}\)
    3. \(\dfrac{1}{4}, \dfrac{9}{5}, \dfrac{11}{3}\)
    4. \(\dfrac{7}{10}, \dfrac{5}{2}, \dfrac{13}{8}, 3\)
    5. \(2 \dfrac{1}{3}, −2 \dfrac{1}{3}\)
    6. \(1 \dfrac{3}{4}, −1 \dfrac{3}{5}\)
    7. \(\dfrac{3}{4}, − \dfrac{3}{4}, 1 \dfrac{2}{3}, −1 \dfrac{2}{3}, \dfrac{5}{2}, − \dfrac{5}{2}\)
    8. \(\dfrac{2}{5}, − \dfrac{2}{5}, 1 \dfrac{3}{4}, −1 \dfrac{3}{4}, \dfrac{8}{3}, − \dfrac{8}{3}\)

    У наступних вправах замовте кожну з наступних пар чисел, використовуючи < or >.

    1. −1__\(− \dfrac{1}{4}\)
    2. −1__\(− \dfrac{1}{3}\)
    3. \(−2 \dfrac{1}{2}\)__− 3
    4. \(−1 \dfrac{3}{4}\)__− 2
    5. \(− \dfrac{5}{12}\)__\(− \dfrac{7}{12}\)
    6. \(− \dfrac{9}{10}\)__\(− \dfrac{3}{10}\)
    7. −3__\(− \dfrac{13}{5}\)
    8. −4__\(− \dfrac{23}{6}\)

    Щоденна математика

    1. Музичні заходи Хореографічний танець розбивається на рахунки. \(\dfrac{1}{1}\)Лічильник має один крок у підрахунку,\(\dfrac{1}{2}\) підрахунок має два кроки в підрахунку, а 1 3 - три кроки в підрахунку. Скільки кроків було б у\(\dfrac{1}{5}\) підрахунку? Який тип підрахунку має чотири кроки в ньому?
    2. Музичні заходи Дроби часто використовуються в музиці. У 4 4 рази є чотири чверті купюри в одному заході.
      1. Скільки заходів зробили б вісім квартальних нот?
      2. Пісня «З Днем Народження тобі» має 25 квартальних нот. Скільки заходів є в «З Днем Народження тебе?»
    3. Випічка Ніна робить п'ять каструлі помадки, щоб служити після музичного концерту. На кожну каструлю їй потрібно 1 2 склянки волоських горіхів.
      1. Скільки чашок волоських горіхів їй потрібно на п'ять каструль помадки?
      2. Як ви вважаєте, простіше виміряти цю суму, коли ви використовуєте неправильний дріб або змішане число? Чому?

    Письмові вправи

    1. Наведіть приклад зі свого життєвого досвіду (поза школою), де важливо було розуміти фракції.
    2. Поясніть, як ви знаходите неправильний дріб\(\dfrac{21}{4}\) на числовому рядку, на якому позначені лише цілі числа від 0 до 10.

    Самостійна перевірка

    (а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

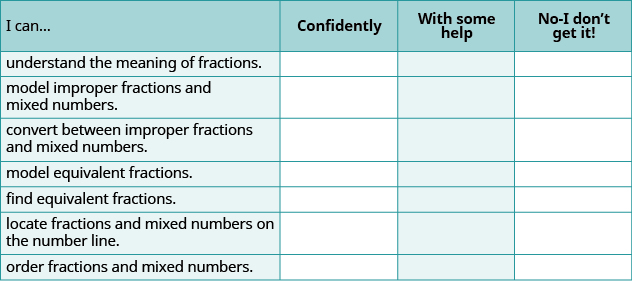
    (b) Якщо більшість ваших перевірок були:

    ... впевнено. Вітаємо! Ви досягли цілей у цьому розділі. Подумайте про навички навчання, які ви використовували, щоб ви могли продовжувати їх використовувати. Що ви зробили, щоб стати впевненим у своїй здатності робити ці речі? Будьте конкретні.

    ... з деякою допомогою. Це потрібно вирішувати швидко, оскільки теми, які ви не освоюєте, стають вибоїнами на вашому шляху до успіху. У математиці кожна тема будується на попередній роботі. Важливо переконатися, що у вас міцний фундамент, перш ніж рухатися далі. До кого можна звернутися за допомогою? Ваші колеги-однокласники та інструктор - хороші ресурси. Чи є в кампусі місце, де доступні репетитори з математики? Чи можна вдосконалити свої навички навчання?

    ... Ні—я цього не розумію! Це попереджувальний знак, і ви не повинні його ігнорувати. Ви повинні отримати допомогу відразу ж, інакше ви швидко будете перевантажені. Зверніться до інструктора, як тільки зможете обговорити вашу ситуацію. Разом ви можете придумати план, щоб отримати вам необхідну допомогу.

    Автори та атрибуція