11.2: Теорія біфуркації

Біфуркація відбувається в нелінійному диференціальному рівнянні, коли невелика зміна параметра призводить до якісної зміни тривалого розв'язку. Прикладами біфуркацій є те, коли нерухомі точки створюються або руйнуються, або змінюють свою стійкість.

(а)

(б)

Малюнок 11.2: Біфуркація сідлового вузла. (а)\(\dot{x}\) проти діаграми\(x ;(b)\) біфуркації.

Розглянуто чотири класичні біфуркації одновимірних нелінійних диференціальних рівнянь: біфуркація сідлових вузлів, транскритична біфуркація, надкритична біфуркація вил та докритична біфуркація вил. Відповідне диференціальне рівняння буде записано як

\[\dot{x}=f_{r}(x), \nonumber \]

де індекс\(r\) представляє параметр, який призводить до біфуркації при зміні на нуль. Найпростіші диференціальні рівняння, які демонструють ці біфуркації, називаються нормальними формами і відповідають локальному аналізу (тобто розширенню рядів Тейлора) більш загальних диференціальних рівнянь навколо фіксованої точки разом з можливим масштабуванням\(x\).

11.2.1. Сідлово-вузол роздвоєння

Переглянути підручник на YouTube

Біфуркація сідлового вузла призводить до створення або руйнування нерухомих точок. Нормальна форма для сідлово-вузла біфуркації задається

\[\dot{x}=r+x^{2} . \nonumber \]

Фіксовані точки є\(x_{*}=\pm \sqrt{-r}\). Зрозуміло, що дві реальні фіксовані точки існують, коли\(r<0\) і не існує реальних фіксованих точок, коли\(r>0\). Стійкість нерухомих точок при\(r<0\) визначенні похідною від\(f(x)=r+x^{2}\), заданої\(f^{\prime}(x)=2 x\). Тому негативна фіксована точка стабільна, а позитивна фіксована точка нестабільна.

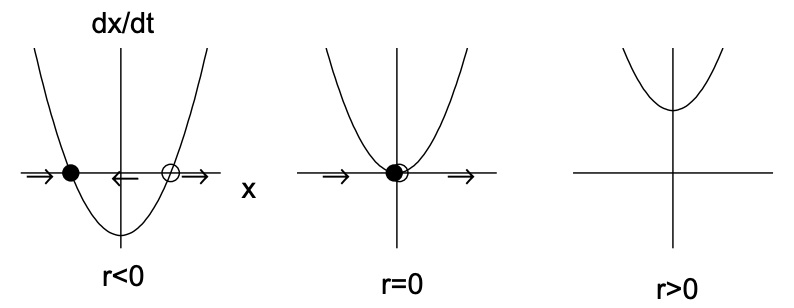
Графічно ми можемо проілюструвати це роздвоєння двома способами. Спочатку на рис. 11.2 (а) ми будуємо\(\dot{x}\) проти\(x\) трьох значень параметрів, що відповідають\(r<0, r=0\) і

(а)

(б)

Малюнок 11.3: Транскритична біфуркація. (а)\(\dot{x}\) проти\(x\); (б) діаграма біфуркації.

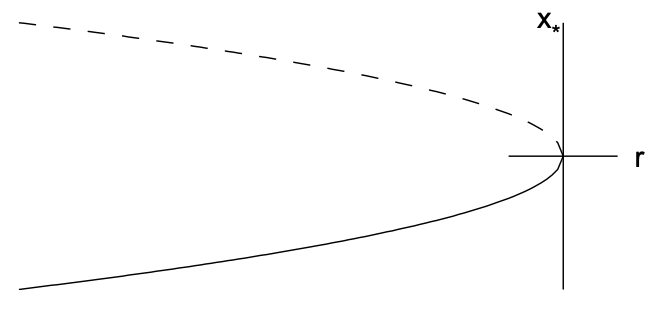
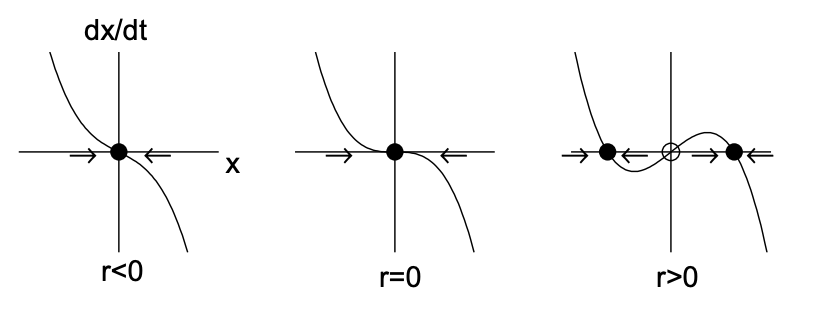
\(r>0\). Значення, при яких\(\dot{x}=0\) відповідають фіксованим точкам, і намальовані стрілки, що вказують на те, як\(x(t)\) розвивається рішення (праворуч якщо\(\dot{x}>0\) і ліворуч, якщо\(\dot{x}<0\)). Стабільна нерухома точка позначається заповненою окружністю, а нестійка фіксована точка - відкритим колом. Зверніть увагу\(r=0\), що коли, розчини сходяться до початку зліва, але розходяться з початком праворуч. По-друге, на рис. 11.2 (б) будуємо діаграму біфуркації, що ілюструє нерухому точку\(x_{*}\) проти параметра біфуркації\(r\). Стабільна фіксована точка позначається суцільною лінією, а нестійку фіксовану точку пунктирною лінією. Зверніть увагу, що дві фіксовані точки стикаються і знищуються\(r=0\), і немає фіксованих точок для\(r>0\).

11.2.2. транскритична біфуркація

Переглянути підручник на YouTube

Транскритична біфуркація виникає, коли відбувається обмін стійкістю між двома нерухомими точками. Нормальна форма для транскритичної біфуркації дається

\[\dot{x}=r x-x^{2} \nonumber \]

Фіксованими точками є\(x_{*}=0\) і\(x_{*}=r\). Похідна від правого боку є\(f^{\prime}(x)=r-2 x\), так що\(f^{\prime}(0)=r\) і\(f^{\prime}(r)=-r\). Тому для\(r<0, x_{*}=0\) стабільна і\(x_{*}=r\) нестабільна, тоді як для\(r>0, x_{*}=r\) стабільна і\(x_{*}=0\) нестабільна. Дві фіксовані точки таким чином обмінюються стабільністю, як\(r\) проходить через нуль. Транскритична біфуркація проілюстрована на рис.11.3.

(а)

(б)

Малюнок 11.4: Надкритична роздвоєння вил. (а)\(\dot{x}\) проти діаграми\(x ;(b)\) біфуркації.

11.2.3. Надкритична роздвоєння вил

Переглянути підручник на YouTube

Біфуркації вил відбуваються у фізичних моделям, де фіксовані точки з'являються і зникають попарно через деяку внутрішню симетрію проблеми. Вила біфуркації можуть бути одного з двох типів. При надкритичної біфуркації пара стійких нерухомих точок створюється в точці біфуркації (або критичної) і існують після (супер) біфуркації. У підкритичній біфуркації в точці біфуркації створюється пара нестійких нерухомих точок і існують перед (суб) біфуркацією.

Нормальну форму для надкритичної біфуркації вил задають

\[\dot{x}=r x-x^{3} . \nonumber \]

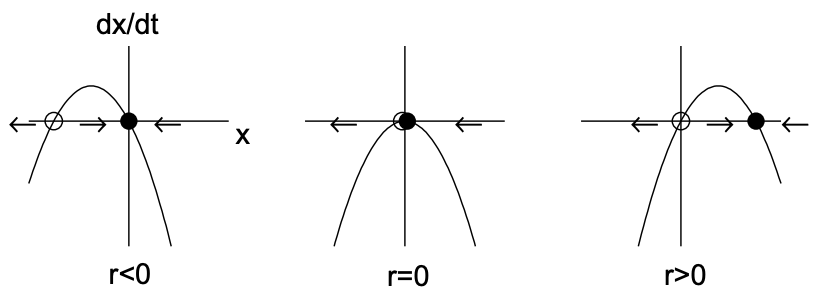
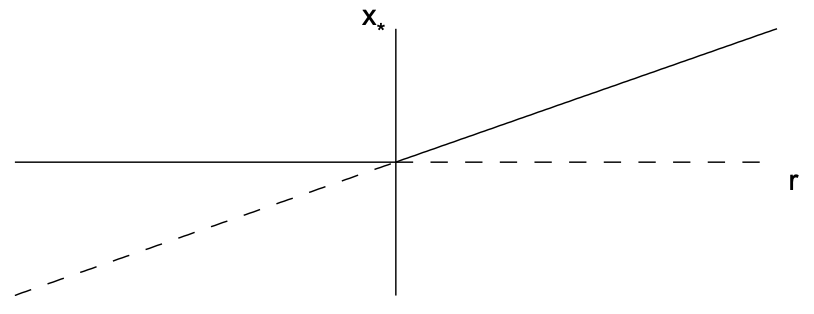
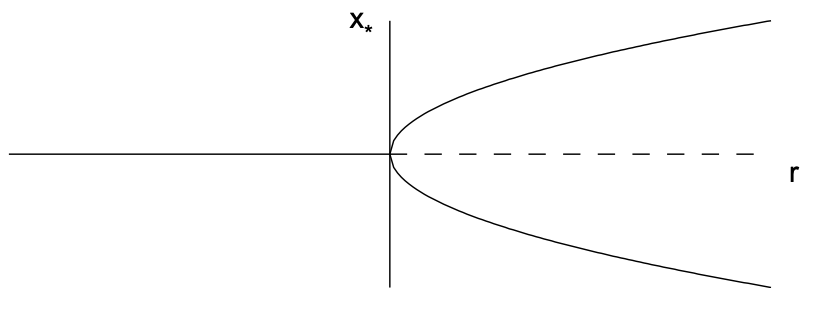
Зауважимо, що лінійний термін призводить до експоненціального зростання, коли\(r>0\) і нелінійний термін стабілізує це зростання. Фіксованими точками є\(x_{*}=0\) і\(x_{*}=\pm \sqrt{r}\), останні нерухомі точки існують тільки тоді, коли\(r>0\). Похідне\(f\) - це\(f^{\prime}(x)=r-3 x^{2}\) так, що\(f^{\prime}(0)=r\) і\(f^{\prime}(\pm \sqrt{r})=-2 r\). Тому\(x_{*}=0\) фіксована точка стабільна\(r<0\) і нестабільна на\(r>0\) той час як фіксовані точки\(x=\pm \sqrt{r}\) існують і стабільні для\(r>0\). Зверніть увагу, що фіксована точка\(x_{*}=0\) стає нестабільною, оскільки\(r\) перетинає нуль і народжуються дві нові стабільні\(x_{*}=\pm \sqrt{r}\) фіксовані точки. Надкритична біфуркація вил проілюстрована на рис.11.4.

11.2.4. Підкритична роздвоєння вил

Переглянути підручник на YouTube

Малюнок 11.5: Підкритична біфуркація вил.

У докритичному випадку кубічний термін є дестабілізуючим. Нормальна форма (на замовлення\(\left.x^{3}\right)\)

\[\dot{x}=r x+x^{3} . \nonumber \]

Фіксованими точками є\(x_{*}=0\) і\(x_{*}=\pm \sqrt{-r}\), останні нерухомі точки існують тільки тоді, коли\(r \leq 0\). Похідна від правого боку\(f^{\prime}(x)=r+3 x^{2}\) така, що\(f^{\prime}(0)=r\) і\(f^{\prime}(\pm \sqrt{-r})=-2 r\). Тому\(x_{*}=0\) фіксована точка стабільна\(r<0\) і нестабільна на\(r>0\) той час як нерухомі точки\(x=\pm \sqrt{-r}\) існують і нестабільні для\(r<0\). Немає стабільних фіксованих точок, коли\(r>0\).

Відсутність стійких фіксованих точок для\(r>0\) вказує на те, що нехтування термінами вищого порядку\(x^{3}\) в\(x\) порівнянні з нормальною формою може бути необґрунтованим. Зберігаючи внутрішню симетрію рівнянь (лише непарні сили\(x\)), можна додати стабілізуючий нелінійний член, пропорційний\(x^{5}\). Розширена нормальна форма (на замовлення\(x^{5}\))

\[\dot{x}=r x+x^{3}-x^{5}, \nonumber \]

і дещо складніше аналізувати. Фіксовані точки - це рішення

\[x\left(r+x^{2}-x^{4}\right)=0 \nonumber \]

Фіксована точка\(x_{*}=0\) існує для всіх\(r\), і чотири додаткові фіксовані точки можна знайти з розв'язків квадратного рівняння в\(x^{2}\):

\[x_{*}=\pm \sqrt{\frac{1}{2}(1 \pm \sqrt{1+4 r})} . \nonumber \]

Ці фіксовані точки існують тільки в\(x_{*}\) тому випадку, якщо вони реальні. Ясна річ, щоб внутрішній квадрат-корінь був справжнім,\(r \geq-1 / 4\). Також спостерігайте, що\(1-\sqrt{1+4 r}\) стає негативним для\(r>0\). Таким чином, ми маємо три інтервали,\(r\) щоб розглянути, і ці регіони та їх фіксовані точки

\[\begin{array}{cl} r<-\frac{1}{4}: & x_{*}=0 \quad \text { (one fixed point); } \\ -\frac{1}{4}<r<0: \quad x_{*}=0, \quad x_{*}=\pm \sqrt{\frac{1}{2}(1 \pm \sqrt{1+4 r})} \quad \text { (five fixed points); } \\ r>0: \quad x_{*}=0, \quad x_{*}=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad \text { (three fixed points). } \end{array} \nonumber \]

Стабільність визначається з\(f^{\prime}(x)=r+3 x^{2}-5 x^{4}\). Тепер,\(f^{\prime}(0)=r\) так\(x_{*}=0\) стабільно\(r<0\) і нестабільно для\(r>0\). Розрахунок для інших чотирьох коренів можна спростити, зазначивши, що\(x_{*}\) задовольняє\(r+x_{*}^{2}-x_{*}^{4}=0\), або\(x_{*}^{4}=r+x_{*}^{2}\). Тому,

\[\begin{aligned} f^{\prime}\left(x_{*}\right) &=r+3 x_{*}^{2}-5 x_{*}^{4} \\ &=r+3 x_{*}^{2}-5\left(r+x_{*}^{2}\right) \\ &=-4 r-2 x_{*}^{2} \\ &=-2\left(2 r+x_{*}^{2}\right) \end{aligned} \nonumber \]

З\(x_{*}^{2}=\frac{1}{2}(1 \pm \sqrt{1+4 r})\), у нас є

\[\begin{aligned} f^{\prime}\left(x_{*}\right) &=-2\left(2 r+\frac{1}{2}(1 \pm \sqrt{1+4 r})\right) \\ &=-((1+4 r) \pm \sqrt{1+4 r}) \\ &=-\sqrt{1+4 r}(\sqrt{1+4 r} \pm 1) \end{aligned} \nonumber \]

Зрозуміло, що плюс корінь завжди стабільний з\(f^{\prime}\left(x_{*}\right)<0\). Мінус корінь існує тільки для\(-\frac{1}{4}<r<0\) і є нестабільним з тих пір\(f^{\prime}\left(x_{*}\right)>0\). Підсумовуємо стійкість різних нерухомих точок:

\[\begin{aligned} & r<-\frac{1}{4}: \quad x_{*}=0 \quad(\text { stable }) \\ & -\frac{1}{4}<r<0: \quad x_{*}=0, \quad \text { (stable) } \\ & x_{*}=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad(\text { stable }) \\ & x_{*}=\pm \sqrt{\frac{1}{2}(1-\sqrt{1+4 r})} \text { (unstable); } \\ & r>0: \quad x_{*}=0 \quad \text { (unstable) } \\ & x_{*}=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad \text { (stable) } . \end{aligned} \nonumber \]

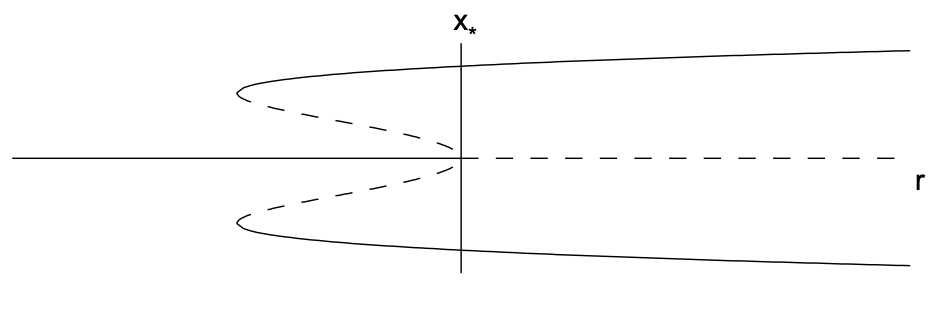
Діаграма біфуркації показана на рис. 11.5, і складається з докритичної біфуркації вил при\(r=0\) і двох сідлово-вузлових біфуркаціях при\(r=-1 / 4\). Ми можемо уявити, що відбувається із\(x\)\(r\) збільшенням негативних значень, припускаючи, що в системі є невеликий шум, який\(x=x(t)\) буде розходитися з нестабільними фіксованими точками. Для\(r<-1 / 4\),\(x\) рівноважне значення є\(x_{*}=0\). У міру\(r\) збільшення в діапазоні\(-1 / 4<r<0, x\) залишиться на\(x_{*}=0\). Однак катастрофа відбувається, як тільки\(r>0\). \(x_{*}=0\)Фіксована точка стає нестійкою, і рішення буде стрибати вгору (або вниз) до єдиної стійкої фіксованої точки. Така поведінка називається біфуркацією стрибка. Подібна катастрофа може трапитися у міру\(r\) зменшення від позитивних значень. При цьому стрибок відбувається відразу ж\(r<-1 / 4\).

Оскільки стабільне рівноважне значення\(x\) залежить від того, збільшуємо ми або\(r\) зменшуємо, ми говоримо, що система проявляє гістерезис. Існування підкритичної біфуркації вил може бути дуже небезпечним в інженерних додатках, оскільки невелика зміна параметрів задачі може призвести до великої зміни стану рівноваги. Фізично це може відповідати обваленню конструкції або виходу з ладу компонента.

11.2.5. Застосування: математична модель рибальства

Переглянути підручник на YouTube

Проілюструється корисність теорії біфуркації шляхом аналізу простої моделі рибного господарства. Ми використовуємо логістичне рівняння (див.\(\S 7.4 .6\)) для моделювання популяції риби за відсутності риболовлі. Для моделювання риболовлі ми припускаємо, що уряд встановив квоти на риболовлю, щоб не більше загальної кількості\(C\) риби на рік може бути виловлено. Ми припускаємо, що коли популяція риби знаходиться на вантажопідйомності навколишнього середовища, рибалка може зловити майже їх повну квоту. Коли популяція риби падає до нижчих значень, рибу може бути важче знайти, і рівень вилову може впасти нижче\(C\), врешті-решт збирається до нуля, оскільки популяція риби зменшується. Поєднуючи логістичне рівняння разом з простою моделлю риболовлі, запропоновано математичну модель

\[\frac{d N}{d t}=r N\left(1-\frac{N}{K}\right)-\frac{C N}{A+N} \nonumber \]

де\(N\) - чисельність популяції риби,\(t\) час,\(r\) - це максимальний потенційний темп зростання популяції риби,\(K\) це вантажопідйомність навколишнього середовища,\(C\) це максимальна швидкість, з якою риба може бути спійманий, і\(A\) є постійним задовольняє\(A<K\), що використовується для моделювання ідеї, що риби стає важче ловити, коли дефіцит.

Ми нерозміреніалізуємо рівняння\ ref {11.4} за допомогою\(x=N / K, \tau=r t, c=C / r K, \alpha=A / K\):

\[\frac{d x}{d \tau}=x(1-x)-\frac{c x}{\alpha+x} . \nonumber \]

Зверніть увагу, що\(0 \leq x \leq 1, c>0\) і\(0<\alpha<1\). Бажаємо якісно описати рівноважні розв'язки рівняння\ ref {11.5} та біфуркації, які можуть виникнути при\(c\) збільшенні швидкості невимірного улову від нуля. Практично, уряд хотів би щороку видавати якомога більшу квоту на вилов, не впливаючи негативно на кількість риби, яка може бути виловлена в наступні роки.

Фіксовані точки рівняння\ ref {11.5} є\(x_{*}=0\) дійсними для всіх\(c\), а розв'язки\(x^{2}-\)\((1-\alpha) x+(c-\alpha)=0\), або

\[x_{*}=\frac{1}{2}\left[(1-\alpha) \pm \sqrt{(1+\alpha)^{2}-4 c}\right] . \nonumber \]

Фіксовані точки, задані Equation\ ref {11.6}, є дійсними, лише якщо\(c<\frac{1}{4}(1+\alpha)^{2}\). Крім того, мінус корінь більше нуля, тільки якщо\(c>\alpha\). Тому нам потрібно розглянути три інтервали, протягом яких існують такі фіксовані точки:

\[\begin{aligned} 0 \leq c \leq \alpha: & x_{*}=0, \quad x_{*}=\frac{1}{2}\left[(1-\alpha)+\sqrt{(1+\alpha)^{2}-4 c}\right] \\ \alpha<c<\frac{1}{4}(1+\alpha)^{2}: & x_{*}=0, \quad x_{*}=\frac{1}{2}\left[(1-\alpha) \pm \sqrt{(1+\alpha)^{2}-4 c}\right] \\ c>\frac{1}{4}(1+\alpha)^{2}: & x_{*}=0 . \end{aligned} \nonumber \]

Стабільність нерухомих точок можна визначити зі строгістю аналітично або графічно. Тут ми просто застосовуємо біологічну інтуїцію разом зі знанням видів одновимірних біфуркацій. Інтуїтивно зрозумілий аргумент робиться простіше, якщо розглядати\(c\) зменшення від великих значень. Коли\(c\) велика, тобто\(c>\frac{1}{4}(1+\alpha)^{2}\) виловлюється занадто багато риби і наша інтуїція говорить про те, що популяція риби вимерла. Тому в цьому інтервалі єдина нерухома точка\(x_{*}=0\) повинна бути стійкою. Як

Малюнок 11.6: Діаграма біфуркації рибного господарства.

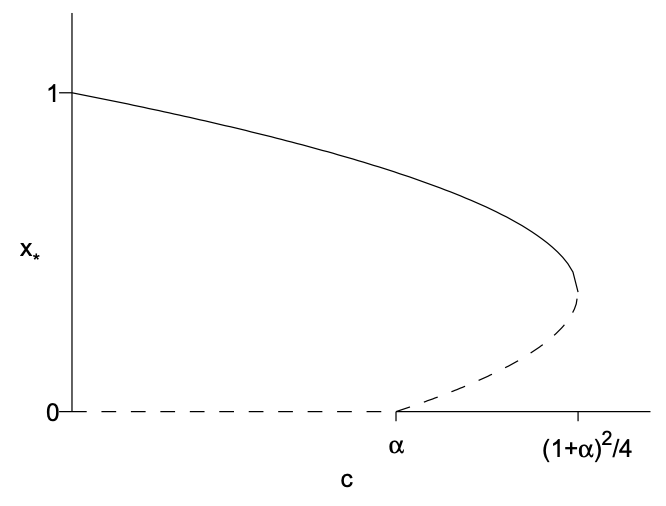
\(c\)зменшується, відбувається біфуркація при\(c=\frac{1}{4}(1+\alpha)^{2}\) введенні двох додаткових нерухомих точок при\(x_{*}=(1-\alpha) / 2\). Тип одновимірної біфуркації, в якій дві нерухомі точки створюються як квадратний корінь, стає реальним, - це сідловудове біфуркація, і одна з нерухомих точок буде стабільною, а інша нестійкою. Слідуючи цим фіксованим точкам\(c \rightarrow 0\), як, ми спостерігаємо, що плюс корінь переходить до одного, який є відповідною стійкою фіксованою точкою, коли немає риболовлі. Тому робимо висновок, що плюсовий корінь стабільний, а мінус - нестабільний. Як\(c\) зменшується далі від цього біфуркації, мінус корінь стикається з фіксованою точкою\(x_{*}=0\) в\(c=\alpha\). Це, здається, транскритична біфуркація, і припускаючи, що відбувається обмін стабільністю, ми повинні мати фіксовану точку, яка\(x_{*}=0\) стає нестабільною для\(c<\alpha\). Отримана діаграма біфуркації показана на рис.11.6.

Мета простих математичних моделей, що застосовуються до складних екологічних проблем, полягає в тому, щоб запропонувати деяке розуміння. Тут ми дізналися, що перелов риби (в моделі\(\left.c>\frac{1}{4}(1+\alpha)^{2}\right)\) протягом одного року потенційно може призвести до раптового краху вилову риби в наступні роки, так що урядам потрібно бути особливо обережними при розгляді збільшення квот на риболовлю.