4: Поведінка поблизу траєкторій - лінеаризація

Тепер ми обговоримо метод аналізу стабільності, який використовує лінеаризацію про об'єкт, стійкість якого представляє інтерес. На даний момент «об'єктами інтересу» є специфічні розв'язки векторного поля. Структура розв'язків лінійних систем постійних коефіцієнтів висвітлена в багатьох підручниках ОДА. Моя улюблена книга Хірша та співав.1. Він охоплює всю лінійну алгебру, необхідну для аналізу лінійних ОД, які ви, ймовірно, не охоплювали у своєму курсі лінійної алгебри. Книга Арнольда також дуже хороша, але презентація більш компактна, з меншою кількістю прикладів.

Почнемо з розгляду загального неавтономного векторного поля:

$$\dot{x} = f(x, t), x \in \mathbb{R}^n, \label{4.1}$$

і ми вважаємо, що

$$\bar{x}(t, t_{0}, x_{0}), \label{4.2}$$

це розв'язок Equation\ ref {4.1}, для якого ми хочемо визначити його властивості стійкості. Коли ми ввели визначення стійкості, ми продовжуємо локалізацію векторного поля про цікавить рішення. Робимо це, вводячи зміну координат.

$x = y+\bar{x}$

для Рівняння\ ref {4.1} наступним чином:

$\dot{x} = \dot{y}+\dot{\bar{x}} = f(y+\bar{x}, t)$,

або

$\dot{y} = f(y+\bar{x}, t)\dot{\bar{x}}$,

$$= f(y+\bar{x}, t)f(\bar{x}, t), \label{4.3}$$

де опускаємо аргументи$\bar{x}(t, t_{0}, x_{0})$ заради менш громіздкого позначення. Далі ми Тейлор$f(y+\bar{x}, t)$ розширюємо$y$ про рішення$\bar{x}$, але ми вимагатимемо лише провідні терміни замовлення явно

$$f(y+\bar{x}, t) = f(\bar{x}, t)+Df(\bar{x},t)y+\mathbb{O}(|y|^2), \label{4.4}$$

де$Df$ позначає похідну (тобто якобійську матрицю) векторної функції f і$\mathbb{O}(|y|^2)$ позначає члени вищого порядку в розширенні Тейлора, які нам не знадобляться в явному вигляді. Підставляючи це в рівняння\ ref {4.4} дає:

$\dot{y} = f(y+\bar{x}, t) - f(\bar{x}, t)$,

$= f(\bar{x}, t)+Df(\bar{x}, t)y+\mathbb{O}(|y|^2)f(\bar{x}, t)$,

$$= Df(\bar{x}, t)y+\mathbb{O}(|y|^2). \label{4.5}$$

Майте на увазі, що нас цікавить поведінка рішень поруч$\bar{x}(t, t_{0}, x_{0})$, тобто для$y$ малих. Тому в цій ситуації здається розумним, що нехтування рівнянням\ ref {4.5} буде наближенням, яке надало б нам конкретну інформацію, яку ми шукаємо.$\mathbb{O}(|y|^2)$ Наприклад, чи надасть нам достатньо інформації для стримування стабільності шахт? Зокрема,

$$\dot{y} = Df(\bar{x}, t)y, \label{4.6}$$

називається лінеаризацією векторного поля$\dot{x} = f (x, t)$ про розв'язку$\bar{x}(t, t_{0}, x_{0})$.

Перш ніж відповісти на питання про те, чи дає Equation\ ref {4.1} адекватне наближення до розв'язків Equation\ ref {4.5} для y «small», ми спочатку вивчимо лінійні векторні поля самостійно.

Лінійні векторні поля також можна класифікувати як неавтономні або автономні. Неавтономні лінійні векторні поля отримані шляхом лінеаризації неавтономного векторного поля навколо розв'язку (і збереження лише лінійних членів). Вони мають загальний вигляд:

$$\dot{y} = A(t)y, y(0) = y_{0}, \label{4.7}$$

де

$$A(t) \equiv Df(\bar{x}(t, t_{0}, x_{0}), t) \label{4.8}$$

являє собою$n \times n$ матрицю. Їх також можна отримати шляхом лінеаризації автономного векторного поля про залежне від часу розв'язку.

Автономне лінійне векторне поле отримують лінеаризацією автономного векторного поля навколо точки рівноваги. Точніше, давайте$\dot{x} = f(x)$ позначимо автономне векторне поле і нехай$x = x_{0}$ позначимо точку рівноваги, т$f(x_{0}) = 0$. Лінеаризоване автономне векторне поле навколо цієї точки рівноваги має вигляд:

$$\dot{y} = Df(x_{0})y, y(0) = y_{0}, \label{4.9}$$

або

$$\dot{y} = Ay, y(0) = y_{0}, \label{4.10}$$

де$A \equiv Df(x_{0})$ -$n \times n$ матриця дійсних чисел. Це важливо, оскільки (4.10) можна вирішити за допомогою методів лінійної алгебри, але Equation\ ref {4.7}, як правило, не може бути вирішено таким чином. Отже, ми зараз опишемо загальне рішення (4.10).

Загальний розв'язок рівняння\ ref {4.10} задається:

$$y(t) = e^{At}y_{0}. \label{4.11}$$

Для того, щоб переконатися, що це рішення, нам просто потрібно замінити в праву сторону і ліву сторону (4.10) і показати, що рівність тримається. Однак спочатку потрібно пояснити, що таке,$e^{At}$ тобто експоненціальна$n \times n$ матриця A (вивчивши Equation\ ref {4.11}, має бути зрозуміло, що якщо Equation\ ref {4.11} має сенс математично, то вона$e^{At}$ повинна бути$n times n$ матрицею).

Так само, як експоненціальна скаляра, експоненціальна матриця визначається через експоненціальний ряд наступним чином:

$e^{At} \equiv \mathbb{I}+At+\frac{1}{2!}A^{2}t^{2}+···+\frac{1}{n!}A^{n}t^{n}+\cdots$,

$$= \sum_{i=0}^{n}\frac{1}{i!}A^{i}t^{i}, \label{4.12}$$

де$\mathbb{I}$ позначає матрицю$n \times n$ ідентичності. Але ми все одно повинні відповісти на питання: «чи має цей експоненціальний ряд із добутками матриць математичний сенс»? Звичайно, ми можемо обчислити добуток матриць і помножити їх на скаляри. Але ми повинні надати сенс нескінченній сумі таких математичних об'єктів. Ми робимо це, визначаючи норму матриці, а потім розглядаючи збіжність ряду в нормі. Коли це робиться, «проблема збіжності» точно така ж, як і експоненціальна скаляра. Тому експоненціальний ряд для матриці сходиться абсолютно для всіх t, і тому його можна диференціювати щодо t за терміном, а отриманий ряд похідних також абсолютно збігається.

Далі ми повинні стверджувати, що Equation\ ref {4.11} є розв'язком Рівняння\ ref {4.10}. Якщо диференціювати термін ряду (4.12) за терміном, ми отримаємо, що:

$$\frac{d}{dt}e^{At} = Ae^{At} = e^{At}A, \label{4.13}$$

де ми використовували той факт, що матриці A і$e^{At}$ коммутіруют (це легко вивести з того, що A комутує з будь-якою потужністю А) Потім з цього розрахунку випливає, що:

$$\dot{y} = \frac{d}{dt}e^{At}y_{0} = Ae^{At}y_{0} = Ay. \label{4.14}$$

Тому загальна задача розв'язання (4.10) еквівалентна обчислювальної$e^{At}$, і ми зараз звернемо свою увагу на це завдання.

По-перше, припустимо, що$A$ це діагональна матриця, скажімо

$$A = \begin{pmatrix} {\lambda_{1}}&{0}&{\cdots}&{0}\\ {0}&{\lambda_{2}}&{\cdots}&{0}\\ {0}&{0}&{\cdots}&{0}\\ {0}&{0}&{\cdots}&{\lambda_{n}} \end{pmatrix} \label{4.15}$$

Тоді легко побачити, підставивши A в експоненціальний ряд (4.12), що:

$$e^{At} = \begin{pmatrix} {e^{\lambda_{1}t}}&{0}&{\cdots}&{0}\\ {0}&{e^{\lambda_{2}t}}&{\cdots}&{0}\\ {0}&{0}&{\cdots}&{0}\\ {0}&{0}&{\cdots}&{e^{\lambda}t} \end{pmatrix} \label{4.16}$$

Тому наша стратегія буде полягати в перетворенні координат так, щоб в нових координатах А стала діагональною (або максимально «наближеною» до діагоналі, що ми пояснимо найближчим часом). Тоді$e^{At}$ буде легко обчислюватися в цих координатах. Після того, як це буде досягнуто, ми використовуємо зворотне перетворення, щоб перетворити рішення назад до вихідної системи координат.

Тепер ми робимо ці ідеї точними. Ми пускаємо

$$y = Tu, u \in \mathbb{R}^n, y \in \mathbb{R}^n, \label{4.17}$$

де T -$n \times n$ матриця, точні властивості якої будуть розроблені в наступному.

Це типовий підхід в ОДУ. Ми пропонуємо загальне координатне перетворення ОДА, а потім будуємо його таким чином, що дає властивості ОДА, які ми бажаємо. Заміна (4.17) на (4.10) дає:

$$\dot{y} = T\dot{u} = Ay = ATu, \label{4.18}$$

T буде побудована таким чином, що робить його оборотним, так що ми маємо:

$$\dot{u} = T^{-1}ATu, u(0) = T^{-1}y(0). \label{4.19}$$

Для спрощення позначення дозволимо:

$$T = T^{-1}AT, \label{4.20}$$

або

$$A = T^{-1}\Lambda T. \label{4.21}$$

Підстановка (4.21) в ряд для матричної експоненціальної (4.12) дає:

$e^{At} = e^{T\Lambda T^{-1}t}$,

$$= \mathbb{1}+ T\Lambda T^{-1}t+\frac{1}{2!}(T\Lambda T^{-1})^{2}t^2+\cdots+\frac{1}{n!}(T\Lambda T^{-1})^{n}t^n+\cdots \label{4.22}$$

Тепер зауважте, що для будь-якого натурального числа n ми маємо:

$(T\Lambda T^{-1})^{n} = \underbrace{(T\Lambda T^{-1})(T\Lambda T^{-1})\cdots (T\Lambda T^{-1})(T\Lambda T^{-1})}_{n factors}$

$$= T\Lambda^{n}T^{-1} \label{4.23}$$

Заміна цього в (4.22) дає:

$e^{At} = \sum_{n=0}^{\infty} \frac{1}{n!}(T\Lambda T^{-1})^{n}t^n$,

$= T(\sum_{n=0}^{\infty} \frac{1}{n!}\Lambda^{n}t^n)T^{-1}$,

$$= Te^{\Lambda t}T^{-1} \label{4.24}$$

або

$$e^{At} = Te^{\Lambda t}T^{-1} \label{4.25}$$

Тепер ми приходимо до нашого основного результату. Якщо Т побудований так, що

$$\Lambda = T^{-1}AT \label{4.26}$$

діагональ, то це випливає з (4.16) і (4.25), які завжди$e^{At}$ можна обчислити. Таким чином, задача ОДА розв'язання (4.10) стає задачею в лінійній алгебрі. Але чи завжди можна діагоналізувати загальну$n \times n$ матрицю А? Якщо у вас був курс лінійної алгебри, ви знаєте, що відповідь на це питання «ні». Існує теорія (реального), яка буде застосовуватися тут. Тим не менш, це призведе нас до занадто великої диверсії для цього курсу. Замість цього ми розглянемо три стандартних випадку для$2 \times 2$ матриць. Цього вистачить для введення основних ідей, не загрузши в лінійній алгебрі. Тим не менш, його не уникнути цілком. Вам потрібно буде вміти обчислювати власні значення і власні вектори$2 \times 2$ матриць, і розуміти їх значення.

Три випадки$2 \times 2$ матриць, які ми розглянемо, характеризуються їх власними значеннями:

• два реальних власних значення, діагональні A,
• два однакових власних значення, недіагональних A,
• складна сполучена пара власних значень.

У наведеній нижче таблиці ми підсумовуємо форму, в яку ці матриці можуть бути перетворені (іменовані як A) і результуючу експоненцію цієї канонічної форми.

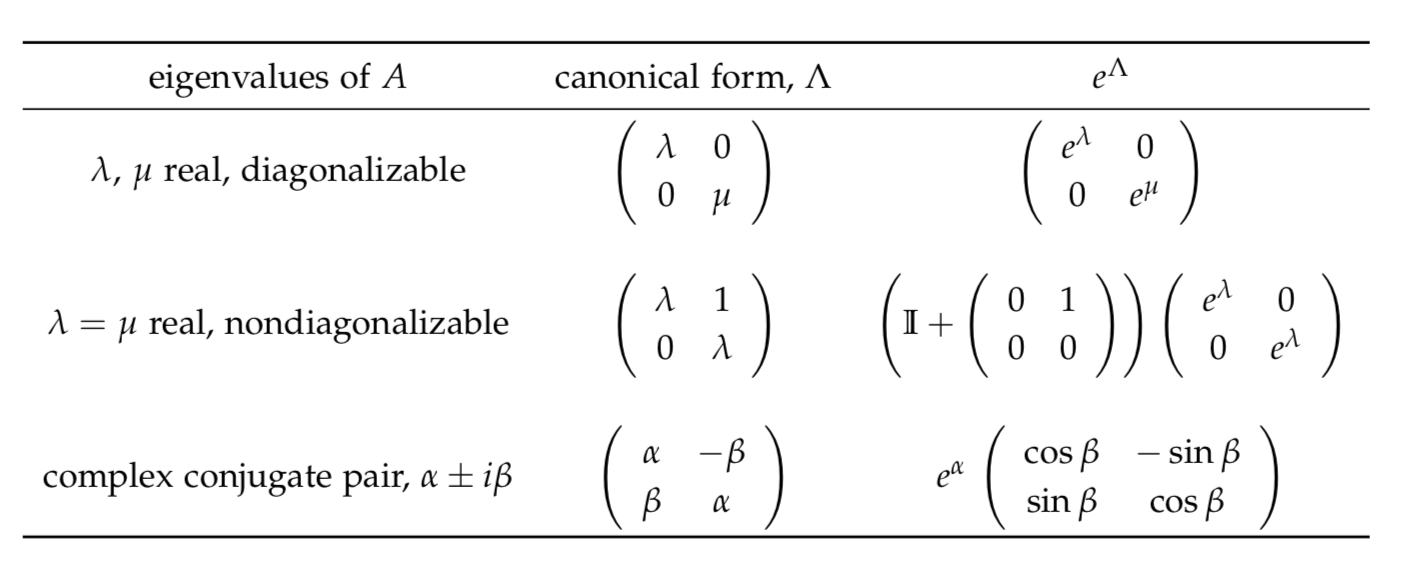
Після того, як трансформація буде$\Lambda$ здійснена, ми будемо використовувати ці результати для виведення$e^{\Lambda}$.