2.5: Точні рівняння
- Page ID
- 62327
У цьому розділі зручно писати диференціальні рівняння першого порядку у вигляді
\[\label{eq:2.5.1} M(x,y)\,dx+N(x,y)\,dy=0.\]
Це рівняння можна інтерпретувати як
\[\label{eq:2.5.2} M(x,y)+N(x,y)\,{dy\over dx}=0,\]
де\(x\) незалежна змінна і\(y\) є залежною змінною, або як
\[\label{eq:2.5.3} M(x,y)\,{dx\over dy}+N(x,y)=0,\]
де\(y\) - незалежна змінна і\(x\) є залежною змінною. Оскільки розв'язки рівняння\ ref {eq:2.5.2} та Equation\ ref {eq:2.5.3} часто доведеться залишати в неявній формі, ми скажемо, що\(F(x,y)=c\) це неявне рішення рівняння\ ref {eq:2.5.1}, якщо кожна диференційовна функція,\(y=y(x)\) яка задовольняє,\(F(x,y)=c\) є розв'язком рівняння\ ref {eq:2.5.2} і кожна диференційовна функція\(x=x(y)\), яка\(F(x,y)=c\) задовольняє, є розв'язком Рівняння\ ref {eq:2.5.3}
Ось кілька прикладів:
| Рівняння\ ref {еква:2.5.1} | Рівняння\ ref {еква:2.5.2} | Рівняння\ ref {еква:2.5.3} |
|---|---|---|
| \(3x^2y^2\,dx+2x^3y\,dy =0\) | \(3x^2y^2+2x^3y\, {dy\over dx} =0\) | \(3x^2y^2\, {dx\over dy}+2x^3y=0\) |
| \((x^2+y^2)\,dx +2xy\,dy=0\) | \((x^2+y^2)+2xy\, {dy\over dx}=0\) | \((x^2+y^2)\, {dx\over dy} +2xy=0\) |
| \(3y\sin x\,dx-2xy\cos x\,dy =0\) | \(3y\sin x-2xy\cos x\, {dy\over dx} =0\) | \(3y\sin x\, {dx\over dy}-2xy\cos x =0\) |
Зауважте, що роздільне рівняння можна записати як Equation\ ref {eq:2.5.1} як
\[M(x)\,dx+N(y)\,dy=0. \nonumber\]
ми розробимо метод розв'язання Equation\ ref {eq:2.5.1} за відповідними\(M\) припущеннями на\(N\) і. Цей метод є розширенням методу поділу змінних. Перш ніж заявити про це, розглянемо приклад.
Покажіть, що
\[\label{eq:2.5.4} x^4y^3+x^2y^5+2xy=c \]
є неявним рішенням
\[\label{eq:2.5.5} (4x^3y^3+2xy^5+2y)\,dx+(3x^4y^2+5x^2y^4+2x)\,dy=0. \]
Рішення
\(y\)Щодо функції\(x\) та диференціювання рівняння\ ref {eq:2.5.4} неявно щодо\(x\) прибутковості
\[(4x^3y^3+2xy^5+2y)+(3x^4y^2+5x^2y^4+2x)\,{dy\over dx}=0. \nonumber\]
Аналогічно,\(x\) щодо функції\(y\) та диференціювання рівняння\ ref {eq:2.5.4} неявно щодо\(y\) прибутковості
\[(4x^3y^3+2xy^5+2y){dx\over dy}+(3x^4y^2+5x^2y^4+2x)=0. \nonumber\]
Тому рівняння\ ref {eq:2.5.4} є неявним розв'язком Equation\ ref {eq:2.5.5} в будь-якій з двох можливих інтерпретацій.
Ви можете подумати, що приклад Template:index не має сенсу, оскільки створення диференціального рівняння, яке має задане неявне рішення, не особливо цікаво. Однак вона ілюструє наступну важливу теорему, яку ми доведемо за допомогою неявної диференціації, як у прикладі Template:index.
Якщо\(F=F(x,y)\) має суцільні часткові похідні\(F_x\) і\(F_y\), то
\[\label{eq:2.5.6} F(x,y)=c \]
(з\(c\) як константа) - неявне рішення диференціального рівняння
\[\label{eq:2.5.7} F_x(x,y)\,dx+F_y(x,y)\,dy=0.\]
- Доказ
-
\(y\)Щодо функції\(x\) та диференціювання рівняння\ ref {eq:2.5.6} неявно щодо\(x\) прибутковості
\[F_x(x,y)+F_y(x,y)\,{dy\over dx}=0. \nonumber\]
З іншого боку, щодо\(x\) функції\(y\) та диференціювання рівняння\ ref {eq:2.5.6} неявно щодо\(y\) прибутковості
\[F_x(x,y)\,{dx\over dy}+F_y(x,y)=0. \nonumber\]
Таким чином, Equation\ ref {eq:2.5.6} є неявним розв'язком Equation\ ref {eq:2.5.7} в будь-якій з двох можливих інтерпретацій.
Ми скажемо, що рівняння
\[\label{eq:2.5.8} M(x,y)\,dx+N(x,y)\,dy=0\]
є точним на відкритому\(R\) прямокутнику, якщо є функція\(F=F(x,y)\) такі\(F_x\) і\(F_y\) є безперервними, і
\[\label{eq:2.5.9} F_x(x,y)=M(x,y) \quad \text{and} \quad F_y(x,y)=N(x,y)\]
для всіх\((x,y)\) в\(R\). Це використання «exact» пов'язане з його використанням у обчисленні, де вираз
\[F_x(x,y)\,dx+F_y(x,y)\,dy\nonumber \]
(отримано шляхом підстановки рівняння\ ref {eq:2.5.9} в ліву частину Рівняння\ ref {eq:2.5.8}) є точним диференціалом\(F\).
Приклад Template:index показує, що легко вирішити Equation\ ref {eq:2.5.8}, якщо воно точне, і ми знаємо функцію\(F\), яка задовольняє Equation\ ref {eq:2.5.9}. Важливими питаннями є:
- Питання 1. З огляду на рівняння Equation\ ref {eq:2.5.8}, як ми можемо визначити, чи є воно точним?
- Питання 2. Якщо рівняння\ ref {eq:2.5.8} є точним, як знайти функцію, що\(F\) задовольняє рівняння\ ref {eq:2.5.9}?
Щоб знайти відповідь на питання 1, припустимо, що існує функція,\(F\) яка задовольняє Equation\ ref {eq:2.5.9} на деякому відкритому прямокутник\(R\), і, крім того, що\(F\) має безперервні змішані часткові похідні\(F_{xy}\) і\(F_{yx}\). Тоді теорема з числення передбачає, що\[\label{eq:2.5.10} F_{xy}=F_{yx}.\] Якщо\(F_x=M\) і\(F_y=N\), диференціюючи перше з цих рівнянь по відношенню до,\(y\) а друге по відношенню до\(x\) прибутковості
\[\label{eq:2.5.11} F_{xy}=M_y \quad \text{and} \quad F_{yx}=N_x.\]
З Рівняння\ ref {eq:2.5.10} і Equation\ ref {eq:2.5.11} ми робимо висновок, що необхідною умовою точності є те, що\(M_y=N_x\). Це мотивує наступна теорема, яку ми констатуємо без доказів.
Припустимо\(N\),\(M\) і є неперервними і мають неперервні часткові похідні\(M_y\) і\(N_x\) на відкритому прямокутнику\(R.\) Тоді
\[M(x,y)\,dx+N(x,y)\,dy=0\nonumber \]
точно,\(R\) якщо і тільки якщо
\[\label{eq:2.5.12} M_y(x,y)=N_x(x,y)\]
для всіх\((x,y)\) в\(R.\).
Щоб допомогти вам запам'ятати умову точності, зауважте, що коефіцієнти\(dx\) і\(dy\) диференційовані в Equation\ ref {eq:2.5.12} щодо «протилежних» змінних; тобто коефіцієнт диференційований відносно\(y\), тоді як коефіцієнт\(dx\) \(dy\)диференційовано по відношенню до\(x\).
Показати, що рівняння
\[3x^2y\,dx+4x^3\,dy=0\nonumber \]
не є точним на будь-якому відкритому прямокутнику.
Рішення
Тут
\[M(x,y)=3x^2y \quad \text{and} \quad N(x,y)=4x^3 \nonumber\]
тому
\[M_y(x,y)=3x^2 \quad \text{and} N_x(x,y)=12 x^2. \nonumber\]
Тому\(M_y=N_x\) на лінії\(x=0\), але не на будь-який відкритий прямокутник, так що немає\(F\) такої функції, що\(F_x(x,y)=M(x,y)\) і\(F_y(x,y)=N(x,y)\) для всіх\((x,y)\) на будь-який відкритий прямокутник.
Наступний приклад ілюструє два можливих методу знаходження функції\(F\), яка задовольняє умові\(F_x=M\) і\(F_y=N\) якщо\(M\,dx+N\,dy=0\) є точною.
Вирішити
\[\label{eq:2.5.13} (4x^3y^3+3x^2)\,dx+(3x^4y^2+6y^2)\,dy=0.\]
Рішення (Спосіб 1)
Тут\[M(x,y)=4x^3y^3+3x^2,\quad N(x,y)=3x^4y^2+6y^2,\nonumber \] і\[M_y(x,y)=N_x(x,y)=12 x^3y^2\nonumber \] для всіх\((x,y)\). Тому теорема Template:index означає, що існує\(F\) така функція, що
\[\label{eq:2.5.14} F_x(x,y)=M(x,y)=4x^3y^3+3x^2\]
і
\[\label{eq:2.5.15} F_y(x,y)=N(x,y)=3x^4y^2+6y^2\]
для всіх\((x,y)\). Щоб знайти\(F\), ми інтегруємо Equation\ ref {eq:2.5.14}\(x\) щодо отримання
\[\label{eq:2.5.16} F(x,y)=x^4y^3+x^3+\phi(y),\]
де\(\phi (y)\) «константа» інтеграції. (\(\phi\)Ось «константа» в тому\(x\), що вона не залежить від змінної інтеграції.) Якщо будь-яка\(\phi\) диференційовна функція,\(y\) то\(F\) задовольняє рівняння\ ref {eq:2.5.14}. Щоб визначити\(\phi\) так, що\(F\) також задовольняє Equation\ ref {eq:2.5.15}, припустимо, що\(\phi\) диференційовний і\(F\) диференційований по відношенню до\(y\). Це дає
\[F_y(x,y)=3x^4y^2+\phi'(y). \nonumber\]
Порівняння цього з рівнянням\ ref {eq:2.5.15} показує, що
\[\phi'(y)=6y^2. \nonumber\]
Ми інтегруємо це відносно\(y\) і приймаємо константу інтеграції рівною нулю, оскільки ми зацікавлені лише у пошуку деяких\(F\), які задовольняють Equation\ ref {eq:2.5.14} та Equation\ ref {eq:2.5.15}. Це дає
\[\phi (y)=2y^3. \nonumber\]
Підставляючи це в рівняння\ ref {eq:2.5.16} дає
\[\label{eq:2.5.17} F(x,y)=x^4y^3+x^3+2y^3.\]
Тепер теорема Template:index передбачає, що\[x^4y^3+x^3+2y^3=c\nonumber \] це неявне рішення рівняння\ ref {eq:2.5.13}. Рішення цього для\(y\) дає явне рішення
\[y=\left(c-x^3\over2+x^4\right)^{1/3}. \nonumber\]
Рішення (Спосіб 2)
Замість того, щоб спочатку інтегрувати Equation\ ref {eq:2.5.14} стосовно\(x\), ми могли б почати з інтеграції Equation\ ref {eq:2.5.15}\(y\) щодо отримання
\[\label{eq:2.5.18} F(x,y)=x^4y^3+2y^3+\psi (x),\]
де\(\psi\) - довільна функція\(x\). Щоб визначити\(\psi\), ми припускаємо, що\(\psi\) диференціюється і\(F\) диференціюється по відношенню до того\(x\), що дає
\[F_x(x,y)=4x^3y^3+\psi'(x). \nonumber\]
Порівняння цього з рівнянням\ ref {eq:2.5.14} показує, що
\[\psi'(x)=3x^2. \nonumber\]
Інтегруючи це і знову приймаючи константу інтеграції, щоб бути нульовою прибутковістю
\[\psi(x)=x^3. \nonumber\]
Підставляючи це в рівняння\ ref {eq:2.5.18} дає рівняння\ ref {eq:2.5.17}.
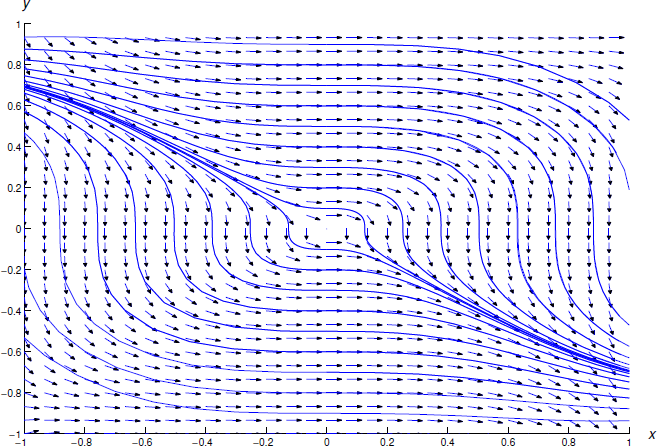
На малюнку Template:index показано поле напряму та деякі інтегральні криві Equation\ ref {eq:2.5.13}.
Ось короткий опис процедури, яка використовується в методі 1 цього прикладу. Ви повинні узагальнити процедуру, використану в способі 2.
- Крок 1. Переконайтеся, що рівняння\[\label{eq:2.5.19} M(x,y)\,dx+N(x,y)\,dy=0\] задовольняє умові точності\(M_y=N_x\). Якщо ні, не йдіть далі з цією процедурою.
- Крок 2. \[{\partial F(x,y)\over\partial x}=M(x,y)\nonumber \]Інтеграція щодо\(x\) отримання,\[\label{eq:2.5.20} F(x,y)=G(x,y)+\phi(y),\] де\(G\) є\(M\) антипохідним щодо\(x\), і\(\phi\) є невідомою функцією\(y\).
- Крок 3. Диференціювати рівняння\ ref {eq:2.5.20}\(y\) щодо отримання\[{\partial F(x,y)\over\partial y}={\partial G(x,y)\over\partial y}+\phi'(y). \nonumber\]
- Крок 4. Прирівняти праву частину цього рівняння до\(N\) і вирішити для\(\phi'\); таким чином,\[{\partial G(x,y)\over\partial y}+\phi'(y)=N(x,y), \quad \text{so} \quad \phi'(y)=N(x,y)-{\partial G(x,y)\over\partial y}. \nonumber\]
- Крок 5. \(\phi'\)Інтегруйте відносно\(y\), приймаючи константу інтеграції рівною нулю, і підставляйте результат в Equation\ ref {eq:2.5.20} для отримання\(F(x,y)\).
- Крок 6. Встановлено\(F(x,y)=c\) для отримання неявного розв'язку Рівняння\ ref {eq:2.5.19}. Якщо можливо,\(y\) вирішуйте для явно як функцію\(x\).
Поширеною помилкою є опущення кроку 6 у наведеній вище процедурі. Однак важливо включити цей крок, оскільки F сам по собі не є розв'язком Equation\ ref {eq:2.5.19}. Багато рівнянь можна зручно розв'язати будь-яким з двох методів, що використовуються в прикладі Template:index. Однак іноді інтеграція, необхідна в одному підході, складніше, ніж в іншому. У таких випадках ми обираємо підхід, який вимагає більш легкої інтеграції.
Розв'яжіть рівняння
\[\label{eq:2.5.21} \left( y e ^ { x y } \tan x + e ^ { x y } \sec ^ { 2 } x \right) d x + x e ^ { x y } \tan x \, dy = 0\]
Рішення
Ми залишаємо це вам, щоб перевірити, що\(M_y = N_x\) на будь-якому відкритому прямокутнику, де\(\tan x\) і\(\sec x\) визначені. Тут ми повинні знайти функцію F таку, що
\[\label{eq:2.5.22} F_x(x, y) = ye^{xy} \tan x + e^{xy} \sec^2 x\]
і
\[\label{eq:2.5.23} F_y(x, y) = xe^{xy} \tan x. \]
Важко інтегрувати Equation\ ref {eq:2.5.22} стосовно\(x\), але легко інтегрувати Equation\ ref {eq:2.5.23} стосовно\(y\). Це дає
\[\label{eq:2.5.24} F(x, y) = e^{xy} \tan x + \psi(x). \]
Диференціація цього щодо\(x\) врожайності
\[F_x(x, y) = y e^{xy} \tan x + e^{xy} \sec^2 x + \psi'(x). \nonumber\]
Порівняння цього з рівнянням\ ref {eq:2.5.22} показує, що\(\psi'(x) = 0\). Отже,\(\psi\) це константа, яку ми можемо прийняти рівною нулю в Equation\ ref {eq:2.5.24}, і
\[e^{xy} \tan x = c, \nonumber\]
є неявним розв'язком Рівняння\ ref {eq:2.5.21}.
Спроба застосувати нашу процедуру до диференціального рівняння, яке не є точним, призведе до невдачі на кроці 4, оскільки функція
\[N - \frac { \partial G } { \partial y } \nonumber\]
не буде незалежним від\(x\) if\(M_y \neq N_x\), і тому не може бути похідною від функції\(y\) поодинці. Приклад Template:index ілюструє це.
Переконайтеся, що рівняння
\[\label{eq:2.5.25} 3x^2y^2\,dx+6x^3y\,dy=0\]
не є точним, і показати, що процедура розв'язання точних рівнянь не вдається при застосуванні до Equation\ ref {eq:2.5.25}.
Рішення
Тут\[M_y(x,y)=6x^2y \quad \text{and} \quad N_x(x,y)=18x^2y,\nonumber \]
тому Рівняння\ ref {eq:2.5.25} не є точним. Проте, спробуємо знайти\(F\) таку функцію, яка
\[\label{eq:2.5.26} F_x(x,y)=3x^2y^2\]
і
\[\label{eq:2.5.27} F_y(x,y)=6x^3y.\]
Інтеграція рівняння\ ref {eq:2.5.26} щодо\(x\) прибутковості
\[F(x,y)=x^3y^2+\phi(y), \nonumber\]
і диференціювання цього щодо\(y\) врожайності
\[F_y(x,y)=2x^3y+\phi'(y). \nonumber\]
Щоб це рівняння відповідало рівнянню\ ref {eq:2.5.27},
\[6x^3y=2x^3y+\phi'(y), \nonumber\]
або
\[\phi'(y)=4x^3y. \nonumber\]
Це протиріччя, тому що\(\phi'\) повинен бути незалежним від\(x\). Тому процедура не вдається.
