2.2: Роздільні рівняння
- Page ID
- 62330
Диференціальне рівняння першого порядку відокремлюється, якщо його можна записати як
\[\label{eq:2.2.1} h(y)y'=g(x),\]
де ліва сторона є твором\(y'\) і функцією,\(y\) а права сторона є функцією\(x\). Перезапис відокремлюваного диференціального рівняння в такому вигляді називається поділом змінних. У розділі 2.1 ми використовували поділ змінних для розв'язання однорідних лінійних рівнянь. У цьому розділі ми застосуємо цей метод до нелінійних рівнянь.
Щоб побачити, як вирішити Equation\ ref {eq:2.2.1}, давайте спочатку припустимо, що\(y\) це рішення. Нехай\(G(x)\) і\(H(y)\) бути антипохідними\(g(x)\) і\(h(y)\); тобто,
\[\label{eq:2.2.2} H'(y)=h(y) \quad \text{and} \quad G'(x)=g(x).\]
Потім, з ланцюгового правила,
\[{d\over dx}H(y(x))=H'(y(x))y'(x)=h(y)y'(x).\nonumber \]
Тому рівняння\ ref {eq:2.2.1} еквівалентно
\[{d\over dx}H(y(x))={d\over dx}G(x).\nonumber \]
Інтеграція обох сторін цього рівняння та об'єднання констант інтеграції дає
\[\label{eq:2.2.3} H(y(x))=G(x)+c.\]
Хоча ми вивели це рівняння на припущенні, що\(y\) є розв'язком Equation\ ref {eq:2.2.1}, тепер ми можемо розглядати його по-іншому: Будь-яка диференційовна функція,\(y\) яка задовольняє Equation\ ref {eq:2.2.3} для деякої константи,\(c\) є розв'язком Рівняння\ ref {eq:2.2.1}. Щоб побачити це, ми диференціюємо обидві сторони Equation\ ref {eq:2.2.3}, використовуючи правило ланцюга зліва, щоб отримати
\[H'(y(x))y'(x)=G'(x), \nonumber \]
що еквівалентно
\[h(y(x))y'(x)=g(x) \nonumber \]
через рівняння\ ref {eq:2.2.2}.
На закінчення, для розв'язання Equation\ ref {eq:2.2.1} достатньо знайти функції\(G=G(x)\)\(H=H(y)\), які задовольняють Equation\ ref {eq:2.2.2}. Тоді будь-яка диференційовна функція\(y=y(x)\), яка задовольняє Рівняння\ ref {eq:2.2.3}, є розв'язком Рівняння\ ref {eq:2.2.1}.
Вирішити рівняння
\[y'=x(1+y^2). \nonumber \]
Рішення
Поділ змінних дає
\[{y'\over 1+y^2}=x. \nonumber \]
Інтеграція врожайності
\[\tan^{-1}y={x^2\over2}+c \nonumber \]
Тому
\[y=\tan\left({x^2\over2}+c\right). \nonumber \]
- Розв'яжіть рівняння\[\label{eq:2.2.4} y'=-{x\over y}.\]
- Вирішити початкову задачу значення\[\label{eq:2.2.5} y'=-{x\over y}, \quad y(1)=1.\]
- Вирішити початкову задачу значення\[\label{eq:2.2.6} y'=-{x\over y}, \quad y(1)=-2.\]
Рішення a
Розділення змінних у рівнянні\ ref {eq:2.2.4} дає
\[yy'=-x. \nonumber \]
Інтеграція врожайності
\[{y^2\over2}=-{x^2\over2}+c, \quad \text{or equivalently} \quad x^2+y^2=2c. \nonumber \]
Останнє рівняння показує, що\(c\) має бути додатним, якщо\(y\) має бути розв'язком Equation\ ref {eq:2.2.4} на відкритому інтервалі. Тому давайте\(2c=a^2\) (з\(a > 0\)) і перепишемо останнє рівняння як
\[\label{eq:2.2.7} x^2+y^2=a^2.\nonumber\]
Це рівняння має два диференційовних\(y\) розв'язку для\(x\):
\[\label{eq:2.2.8} y=\phantom{-} \sqrt{a^2-x^2}, \quad -a < x < a,\nonumber\]
і
\[\label{eq:2.2.9} y= - \sqrt{a^2-x^2}, \quad -a < x < a.\]
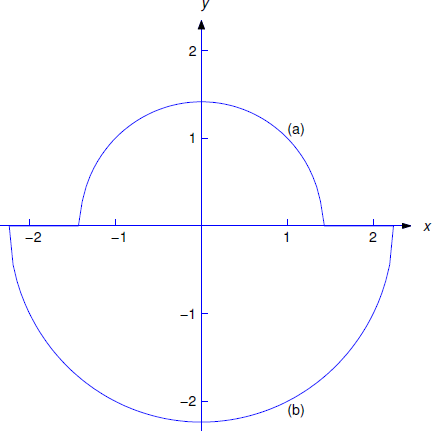
Криві розв'язку, визначені Equation\ ref {eq:2.2.8}, є півколами над\(x\) віссю -і ті, що визначені Equation\ ref {eq:2.2.9}, є півколами нижче\(x\) -осі (Рисунок Template:index).
Рішення б
Розв'язок Рівняння\ ref {eq:2.2.5} є додатним, коли\(x=1\); отже, воно має вигляд Equation\ ref {eq:2.2.8}. Заміна\(x=1\) і\(y=1\) в рівняння\ ref {eq:2.2.7} для задоволення початкової умови дає\(a^2=2\); отже, розв'язок Рівняння\ ref {eq:2.2.5} є
\[y=\sqrt{2-x^2}, \quad - \sqrt{2}< x < \sqrt{2}. \nonumber \]
Рішення c
Розв'язок Рівняння\ ref {eq:2.2.6} є від'ємним, коли\(x=1\) і, отже, має вигляд Рівняння\ ref {eq:2.2.9}. Заміна\(x=1\) і\(y=-2\) в рівняння\ ref {eq:2.2.7} для задоволення початкової умови дає\(a^2=5\). Отже, розв'язок рівняння\ ref {eq:2.2.6} є
\[y=- \sqrt{5-x^2}, \quad -\sqrt{5} < x < \sqrt{5}. \nonumber \]
Неявні розв'язки роздільних рівнянь
У прикладах Template:index та Template:index нам вдалося\(H(y)=G(x)+c\) розв'язати рівняння для отримання явних формул для розв'язків заданих відокремлених диференціальних рівнянь. Як ми побачимо в наступному прикладі, це не завжди можливо. У цій ситуації ми повинні розширити наше визначення розв'язку відокремлюваного рівняння. Наступна теорема дає підставу для цієї модифікації. Опускаємо доказ, який вимагає результату від розширеного числення, що називається теоремою неявної функції.
Припустимо,\(g=g(x)\) є безперервним на\((a,b)\) і\(h=h(y)\) є безперервним на\((c,d).\)\(G\) Дозволяти бути антипохідним від\(g\) on\((a,b)\) і нехай\(H\) бути антипохідним від\(h\) на\((c,d).\)\(x_0\) Дозволяти бути довільною точкою в\((a,b),\) нехай\(y_0\) бути a вказують на\((c,d)\) таке, що\(h(y_0)\ne0,\) і визначити
\[\label{eq:2.2.10} c=H(y_0)-G(x_0).\]
Тоді є функція,\(y=y(x)\) визначена на деякому відкритому інтервалі,\((a_1,b_1),\) де\(a\le a_1<x_0<b_1\le b,\) такі, що\(y(x_0)=y_0\) і
\[\label{eq:2.2.11} H(y)=G(x)+c\]
для\(a_1<x<b_1\). Тому\(y\) є розв'язком початкової задачі значення.
\[\label{eq:2.2.12} h(y)y'=g(x),\quad y(x_0)=y_0.\]
Зручно сказати, що Equation\ ref {eq:2.2.11} з\(c\) довільним є неявним рішенням\(h(y)y'=g(x)\). Криві, визначені рівнянням\ ref {eq:2.2.11}, є інтегральними кривими\(h(y)y'=g(x)\). Якщо\(c\) відповідає рівнянню\ ref {eq:2.2.10}, скажемо, що Equation\ ref {eq:2.2.11} є неявним розв'язком початкової задачі Equation\ ref {eq:2.2.12}. Однак майте на увазі ці моменти:
- Для деяких варіантів може не бути жодних диференційовних\(c\) функцій\(y\), які задовольняють Equation\ ref {eq:2.2.11}.
- Функція\(y\) в Equation\ ref {eq:2.2.11} (не рівняння\ ref {eq:2.2.11} власне) є розв'язком\(h(y)y'=g(x)\).
- Знайти неявні рішення\[\label{eq:2.2.13} y'={2x+1\over5y^4+1}.\]
- Знайдіть неявне рішення\[\label{eq:2.2.14} y'={2x+1\over5y^4+1},\quad y(2)=1.\]
Рішення a
Поділ змінних дає
\[(5y^4+1)y'=2x+1. \nonumber \]
Інтеграція дає неявне рішення
\[\label{eq:2.2.15} y^5+y=x^2+x+ c. \]
рівняння\ ref {еква:2.2.13}.
Рішення б
Накладення початкової умови\(y(2)=1\) в Equation\ ref {eq:2.2.15} дає\(1+1=4+2+c\), отже\(c=-4\). Тому
\[y^5+y=x^2+x-4 \nonumber \]
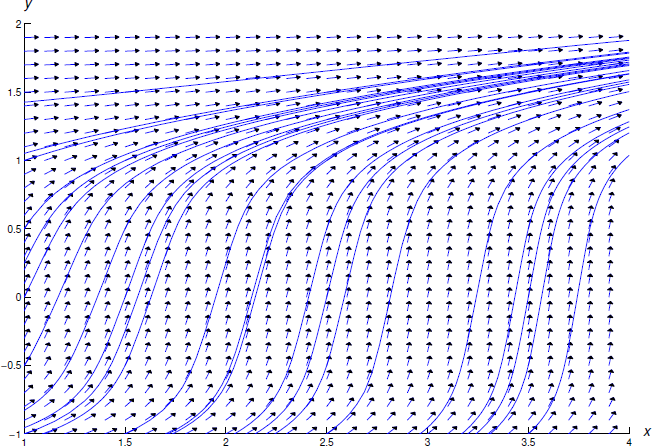
є неявним розв'язком початкової задачі Рівняння\ ref {eq:2.2.14}. Хоча більше однієї диференційовної функції\(y=y(x)\) задовольняє Equation\ ref {eq:2.2.13} поблизу\(x=1\), можна показати, що існує лише одна така функція, яка задовольняє початковій умові\(y(1)=2\). На малюнку Template:index показано поле напряму та деякі інтегральні криві для Equation\ ref {eq:2.2.13}.
Постійні розв'язки роздільних рівнянь
Рівняння форми
\[y'=g(x)p(y) \nonumber \]
є відокремлюваним, оскільки його можна переписати як
\[{1\over p(y)}y'=g(x). \nonumber \]
Однак поділ на не\(p(y)\) є законним, якщо\(p(y)=0\) для деяких значень\(y\). Наступні два приклади показують, як боротися з цією проблемою.
Знайти всі рішення
\[\label{eq:2.2.16} y'=2xy^2.\]
Рішення
Тут ми повинні\(p(y)=y^2\) розділити на окремі змінні. Це не є законним, якщо\(y\) це рішення рівняння\ ref {eq:2.2.16}, що дорівнює нулю для деякого значення\(x\). Одне з таких рішень можна знайти при огляді:\(y \equiv 0\). Тепер припустимо,\(y\) це рішення рівняння\ ref {eq:2.2.16}, яке не однаково нуль. Оскільки\(y\) є безперервним, повинен бути інтервал, на якому ніколи не\(y\) дорівнює нулю. Оскільки ділення на\(y^2\) є законним для\(x\) цього інтервалу, ми можемо розділити змінні в Equation\ ref {eq:2.2.16} для отримання
\[{y'\over y^2}=2x. \nonumber \]
Інтеграція цієї врожайності
\[-{1\over y}=x^2+c, \nonumber \]
що еквівалентно
\[\label{eq:2.2.17} y=-{1\over x^2+c}.\]
Тепер ми показали, що якщо\(y\) це рішення рівняння\ ref {eq:2.2.16}, яке не є однаковим нулем, то\(y\) має бути вигляду Equation\ ref {eq:2.2.17}. Підставивши рівняння\ ref {eq:2.2.17} на рівняння\ ref {eq:2.2.16}, ви можете переконатися, що рівняння\ ref {eq:2.2.17} є розв'язком рівняння\ ref {eq:2.2.16}. Таким чином, розв'язками Рівняння\ ref {eq:2.2.16} є\(y\equiv0\) і функції виду Рівняння\ ref {eq:2.2.17}. Зауважте, що рішення\(y\equiv0\) не має вигляду Equation\ ref {eq:2.2.17} для будь-якого значення\(c\).
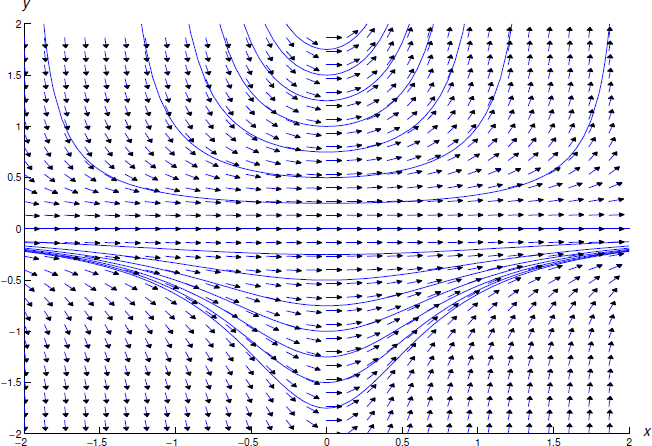
На малюнку Template:index показано поле напряму та деякі інтегральні криві для Рівняння\ ref {eq:2.2.16}
Знайти всі рішення
\[\label{eq:2.2.18} y'={1\over2}x(1-y^2). \]
Тут ми повинні\(p(y)=1-y^2\) розділити на окремі змінні. Це не є законним, якщо\(y\) є розв'язком рівняння\ ref {eq:2.2.18}, що дорівнює\(\pm1\) деякому значенню\(x\). Два таких рішення можна знайти при огляді:\(y \equiv 1\) і\(y\equiv-1\). Тепер припустимо,\(y\) це рішення рівняння\ ref {eq:2.2.18} таке, що\(1-y^2\) не однаково нуль. Оскільки\(1-y^2\) є безперервним, повинен бути інтервал, на якому ніколи не\(1-y^2\) дорівнює нулю. Оскільки ділення на\(1-y^2\) є законним для\(x\) цього інтервалу, ми можемо розділити змінні в Equation\ ref {eq:2.2.18} для отримання
\[{2y'\over y^2-1}=-x. \nonumber \]
Часткове розширення фракції на ліву врожайність
\[\left[{1\over y-1}-{1\over y+1}\right]y'=-x, \nonumber \]
та інтеграція врожайності
\[\ln\left|{y-1\over y+1}\right|=-{x^2\over2}+k; \nonumber \]
отже,
\[\left|{y-1\over y+1}\right|=e^ke^{-x^2/2}. \nonumber \]
Оскільки\(y(x)\ne\pm1\)\(x\) на обговорюваному інтервалі кількість\((y-1)/(y+1)\) не може змінити знак у цьому інтервалі. Тому ми можемо переписати останнє рівняння як
\[{y-1\over y+1}=ce^{-x^2/2}, \nonumber \]
де\(c=\pm e^k\), в залежності від знака\((y-1)/(y+1)\) про інтервал. Рішення для\(y\) врожайності
\[\label{eq:2.2.19} y={1+ce^{-x^2/2}\over 1-ce^{-x^2/2}}. \]
Тепер ми показали, що якщо\(y\) це рішення рівняння\ ref {eq:2.2.18}, яке не однаково дорівнює\(\pm1\), то\(y\) має бути таким, як у Equation\ ref {eq:2.2.19}. Підставивши рівняння\ ref {eq:2.2.19} на рівняння\ ref {eq:2.2.18}, ви можете переконатися, що рівняння\ ref {eq:2.2.19} є розв'язком рівняння\ ref {eq:2.2.18}. Таким чином, розв'язками Рівняння\ ref {eq:2.2.18} є\(y\equiv1\)\(y\equiv-1\) і функції виду Equation\ ref {eq:2.2.19}. Зверніть увагу, що постійний розчин\(y \equiv 1\) можна отримати з цієї формули, взявши\(c=0\); однак інший\(y \equiv -1\) постійний розчин не може бути отриманий таким чином.
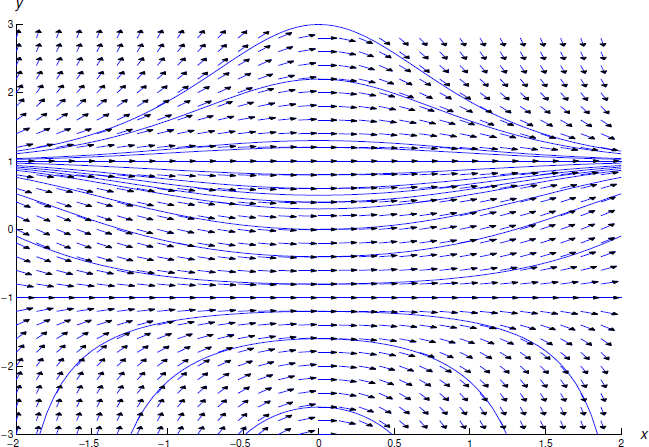
На малюнку Template:index показано поле напряму та деякі інтеграли для Equation\ ref {eq:2.2.18}.
Відмінності між лінійними та нелінійними рівняннями
Теорема 2.1.2 стверджує, що якщо\(p\) і\(f\) є неперервними,\((a,b)\) то кожне розв'язання
\[y'+p(x)y=f(x) \nonumber \]
on\((a,b)\) можна отримати, вибравши значення для константи\(c\) в загальному розв'язку, а якщо\(x_0\) будь-яка точка в\((a,b)\) і\(y_0\) є довільною, то початкова задача значення
\[y'+p(x)y=f(x),\quad y(x_0)=y_0 \nonumber \]
має рішення на\((a,b)\).
Невірно для нелінійних рівнянь. По-перше, ми побачили в прикладах Template:index} та Template:index, що нелінійне рівняння може мати розв'язки, які неможливо отримати шляхом вибору конкретного значення константи, що з'являється в однопараметричному сімействі розв'язків. По-друге, взагалі неможливо визначити інтервал валідності розв'язку задачі початкового значення для нелінійного рівняння простим дослідженням рівняння, оскільки інтервал валідності може залежати від початкової умови. Наприклад, у прикладі Template:index ми побачили, що рішення
\[{dy\over dx}=-{x\over y},\quad y(x_0)=y_0 \nonumber \]
діє на\((-a,a)\), де\(a=\sqrt{x_0^2+y_0^2}\).
Вирішити початкову задачу значення
\[y'=2xy^2, \quad y(0)=y_0 \nonumber \]
і визначити інтервал дії розчину.
Рішення
Спочатку припустимо\(y_0\ne0\). З Прикладу Template:index, ми знаємо, що\(y\) має бути форми
\[\label{eq:2.2.20} y=-{1\over x^2+c}.\]
Накладення початкової умови показує, що\(c=-1/y_0\). Підставляючи це на рівняння\ ref {eq:2.2.20} і перестановка термінів дає рішення
\[y= {y_0\over 1-y_0x^2}. \nonumber \]
Це також рішення, якщо\(y_0=0\). Якщо\(y_0<0\), знаменник не дорівнює нулю для будь-якого значення\(x\), отже, рішення є дійсним\((-\infty,\infty)\). Якщо\(y_0>0\), рішення діє тільки на\((-1/\sqrt{y_0},1/\sqrt{y_0})\).
