8.2: Одновимірні біфуркації
- Page ID
- 61303
Біфуркація відбувається в нелінійному диференціальному рівнянні, коли невелика зміна параметра призводить до якісної зміни тривалого розв'язку. Прикладами біфуркацій є те, коли нерухомі точки створюються або руйнуються, або змінюють свою стійкість.
Розглянуто чотири класичні біфуркації одновимірних нелінійних диференціальних рівнянь: біфуркація сідлових вузлів, транскритична біфуркація, надкритична біфуркація вил та докритична біфуркація вил. Відповідне диференціальне рівняння буде записано так,\[\overset{.}{x}=f_r(x),\nonumber\] де індекс\(r\) представляє параметр, який призводить до біфуркації при зміні через нуль. Найпростіші диференціальні рівняння, які демонструють ці біфуркації, називаються нормальними формами і відповідають локальному аналізу (тобто розширенню рядів Тейлора) більш загальних диференціальних рівнянь навколо фіксованої точки разом з можливим масштабуванням\(x\).
Сідло-вузол роздвоєння
Переглянути підручник на YouTube
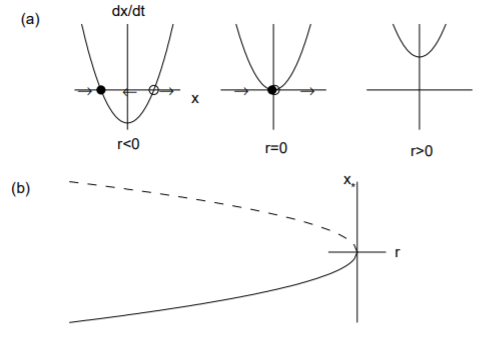
Біфуркація сідлового вузла призводить до створення або руйнування нерухомих точок. Нормальна форма для сідлово-вузла біфуркації дається шляхом\[\overset{.}{x}=r+x^2.\nonumber\]
Фіксовані точки є\(x_* = ±\sqrt{-r}\). Зрозуміло, що дві реальні фіксовані точки існують, коли\(r < 0\) і не існує реальних фіксованих точок, коли\(r > 0\). Стійкість нерухомих точок при\(r < 0\) визначенні похідною від\(f(x) = r + x^2\), заданої\(f' (x) = 2x\). Тому негативна фіксована точка стабільна, а позитивна фіксована точка нестабільна.
Графічно ми можемо проілюструвати це роздвоєння двома способами. По-перше, на рис. \(\PageIndex{1}\)(a), ми будуємо\(\overset{.}{x}\) проти\(x\) для трьох значень параметрів, що відповідають\(r < 0\),\(r = 0\) і\(r > 0\). Значення, при яких\(\overset{.}{x} = 0\) відповідають фіксованим точкам, і намальовані стрілки, що вказують на те, як\(x(t)\) розвивається рішення (праворуч якщо\(\overset{.}{x}> 0\) і ліворуч, якщо\(\overset{.}{x}< 0\)). Стабільна нерухома точка позначається заповненою окружністю, а нестійка фіксована точка - відкритим колом. Зверніть увагу\(r = 0\), що коли, розчини сходяться до початку зліва, але розходяться з початком праворуч. По-друге, на рис. \(\PageIndex{1}\)(б) ми будуємо діаграму біфуркації, що ілюструє фіксовану точку\(x_*\) проти параметра біфуркації\(r\). Стабільна фіксована точка позначається суцільною лінією, а нестійку фіксовану точку пунктирною лінією. Зверніть увагу, що дві фіксовані точки стикаються і знищуються\(r = 0\), і немає фіксованих точок для\(r > 0\).
Транскритична біфуркація
Переглянути підручник на YouTube
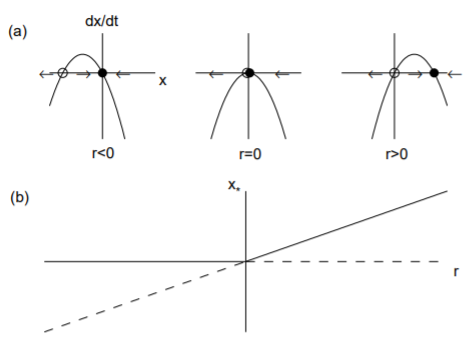
Транскритична біфуркація виникає, коли відбувається обмін стійкістю між двома нерухомими точками. Нормальна форма для транскритичної біфуркації дається шляхом\[\overset{.}{x}=rx-x^2.\nonumber\]
Фіксованими точками є\(x_* = 0\) і\(x_* = r\). Похідна від правого боку є\(f' (x) = r − 2x\), так що\(f' (0) = r\) і\(f ' (r) = −r\). Тому для\(r < 0\),\(x_* = 0\) є стабільним і\(x_* = r\) нестабільним, в той час як для\(r > 0\),\(x_* = r\) є стабільним і\(x_* = 0\) нестабільним. Дві фіксовані точки таким чином обмінюються стабільністю, як\(r\) проходить через нуль. Транскритична біфуркація проілюстрована на рис. \(\PageIndex{2}\).
Надкритичне роздвоєння вил
Переглянути підручник на YouTube
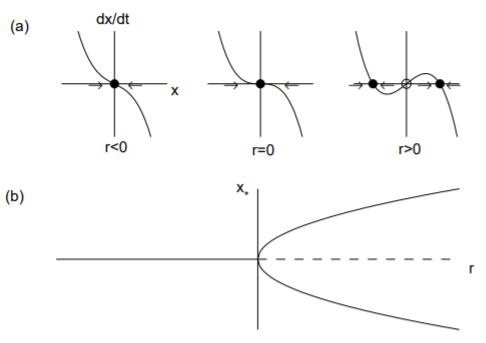
Біфуркації вил відбуваються у фізичних моделям, де фіксовані точки з'являються і зникають попарно через деяку внутрішню симетрію проблеми. Вила біфуркації можуть бути одного з двох типів. При надкритичної біфуркації пара стійких нерухомих точок створюється в точці біфуркації (або критичної) і існують після (супер) біфуркації. У підкритичній біфуркації в точці біфуркації створюється пара нестійких нерухомих точок і існують перед (суб) біфуркацією.
Нормальна форма для надкритичного роздвоєння вил дається шляхом\[\overset{.}{x}=rx-x^3.\nonumber\]
Зауважимо, що лінійний термін призводить до експоненціального зростання, коли\(r > 0\) і нелінійний термін стабілізує це зростання. Фіксованими точками є\(x_* = 0\) і\(x_* = ±\sqrt{r}\), останні нерухомі точки існують тільки тоді, коли\(r > 0\). Похідна\(f\) - це\(f' (x) = r − 3x^2\) так, що\(f' (0) = r\) і\(f' (±\sqrt{r}) = −2r\). Тому\(x_* = 0\) фіксована точка стабільна\(r < 0\) і нестабільна на\(r > 0\) той час як фіксовані точки\(x = ±\sqrt{r}\) існують і стабільні для\(r > 0\). Зверніть увагу, що фіксована точка\(x_* = 0\) стає нестабільною, оскільки\(r\) перетинає нуль і народжуються дві нові стабільні\(x_* = ±\sqrt{r}\) фіксовані точки. Надкритична біфуркація вил проілюстрована на рис. \(\PageIndex{3}\).
Надкритичне роздвоєння вил
Переглянути підручник на YouTube
У докритичному випадку кубічний термін є дестабілізуючим. Нормальна форма (на замовлення\(x^3\)) - це\[\overset{.}{x}=rx+x^3.\nonumber\]
Фіксованими точками є\(x_* = 0\) і\(x_* = ±\sqrt{-r}\), останні нерухомі точки існують тільки тоді, коли\(r ≤ 0\). Похідна від правого боку\(f' (x) = r +3x^2\) така, що\(f' (0) = r\) і\(f' (±\sqrt{-r}) = −2r\). Тому\(x_* = 0\) фіксована точка стабільна\(r < 0\) і нестабільна на\(r > 0\) той час як нерухомі точки\(x = ±\sqrt{-r}\) існують і нестабільні для\(r < 0\). Немає стабільних фіксованих точок, коли\(r > 0\).
Відсутність стійких фіксованих точок для\(r > 0\) вказує на те, що нехтування термінами вищого порядку\(x^3\) в\(x\) порівнянні з нормальною формою може бути необґрунтованим. Зберігаючи внутрішню симетрію рівнянь (лише непарні сили\(x\)), можна додати стабілізуючий нелінійний член, пропорційний\(x^5\). Розширена нормальна форма (на замовлення\(x^5\)) є\[\overset{.}{x}=rx+x^3-x^5,\nonumber\] і дещо складніше аналізувати. Фіксовані точки - це рішення\[x(r+x^2-x^4)=0.\nonumber\]
Фіксована точка\(x_* = 0\) існує для всіх\(r\), і чотири додаткові фіксовані точки можна знайти з розв'язків квадратного рівняння в\(x^2\):
\[x_*=\pm\sqrt{\frac{1}{2}(1\pm\sqrt{1+4r})}.\nonumber\]
Ці фіксовані точки існують тільки в\(x_*\) тому випадку, якщо вони реальні. Ясна річ, щоб внутрішній квадрат-корінь був справжнім,\(r ≥ −1/4\). Також спостерігайте, що\(1 −\sqrt{1+4r}\) стає негативним для\(r > 0\). Таким чином, ми маємо три інтервали,\(r\) щоб розглянути, і ці регіони та їх фіксовані точки\[\begin{array}{rlll} r<-\frac{1}{4}: & x_*=0 &\text{(one fixed point);} \\ -\frac{1}{4}<r<0: & x_*=0, &x_*=\pm\sqrt{\frac{1}{2}(1\pm\sqrt{1+4r})} &\text{(five fixed points);} \\ r>0: &x_*=0, &x_*=\pm\sqrt{\frac{1}{2}(1+\sqrt{1+4r})} &\text{(three fixed points).}\end{array}\nonumber\]
Стабільність визначається з\(f' (x) = r + 3x^2 − 5x^4\). Тепер,\(f' (0) = r\) так\(x_* = 0\) стабільно\(r < 0\) і нестабільно для\(r > 0\). Розрахунок для інших чотирьох коренів можна спростити, зазначивши, що\(x_*\) задовольняє\(r + x_*^2 − x_*^4 = 0\), або\(x_*^4 = r + x_*^2\). Тому,\[\begin{aligned}f'(x_*)&=r+3x_*^2-5x_*^4 \\ &=r+3x_*^2-5(r+x_*^2) \\ &=-4r-2x_*^2 \\ &=-2(2r+x_*^2).\end{aligned}\]
З\(x_*^2=\frac{1}{2}(1\pm\sqrt{1+4r})\), у нас є\[\begin{aligned} f'(x_*)&=-2\left(2r+\frac{1}{2}(1\pm\sqrt{1+4r})\right) \\ &=-\left( (1+4r)\pm\sqrt{1+4r}\right) \\ &=-\sqrt{1+4r}\left(\sqrt{1+4r}\pm 1\right).\end{aligned}\]
Зрозуміло, що плюс корінь завжди стабільний з\(f' (x_*) < 0\). Мінус корінь існує тільки для\(−\frac{1}{4}< r < 0\) і є нестабільним з тих пір\(f' (x_*) > 0\). Підсумовуємо стійкість різних нерухомих точок:
\[\begin{array}{rll} r<-\frac{1}{4}:&x_*=0&\text{(stable);} \\ -\frac{1}{4}<r<0:&x_*=0,&\text{(stable)} \\ &x_*=\pm\sqrt{\frac{1}{2}(1+\sqrt{1+4r})}&\text{(stable);} \\ &x_*=\pm\sqrt{\frac{1}{2}(1-\sqrt{1+4r})}&\text{(unstable);} \\ r>0:&x_*=0&\text{(unstable)} \\ &x_*=\pm\sqrt{\frac{1}{2}(1+\sqrt{1+4r})}&\text{(stable).}\end{array}\nonumber\]
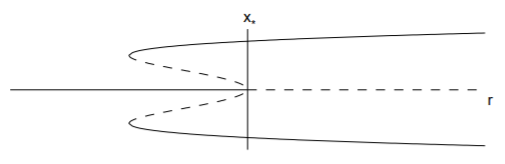
Схема роздвоєння показана на рис. \(\PageIndex{4}\), І складається з субкритичної вил біфуркації при\(r = 0\) і двох сідлово-вузлів біфуркацій при\(r = −1/4\). Ми можемо уявити, що відбувається із\(x\)\(r\) збільшенням негативних значень, припускаючи, що в системі є невеликий шум, який\(x = x(t)\) буде розходитися з нестабільними фіксованими точками. Для\(r < −1/4\),\(x\) рівноважне значення є\(x_* = 0\). У міру\(r\) збільшення діапазону\(−1/4 < r < 0\),\(x\) залишиться на\(x_* = 0\). Однак катастрофа відбувається відразу ж\(r > 0\). \(x_* = 0\)Фіксована точка стає нестійкою, і рішення буде стрибати вгору (або вниз) до єдиної стійкої фіксованої точки. Така поведінка називається роздвоєнням стрибка. Подібна катастрофа може статися у міру\(r\) зменшення від позитивних значень. При цьому стрибок відбувається відразу ж\(r < −1/4\).
Оскільки стабільне рівноважне значення\(x\) залежить від того, збільшуємо ми або\(r\) зменшуємо, ми говоримо, що система проявляє гістерезис. Існування підкритичної біфуркації вил може бути дуже небезпечним в інженерних додатках, оскільки невелика зміна параметрів задачі може призвести до великої зміни стану рівноваги. Фізично це може відповідати обваленню конструкції або виходу з ладу компонента.
