2.2: Теорема SAS

Last updated
Save as PDF

Page ID: 58823

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми говорили, що два трикутники є конгруентними, якщо всі їхні сторони і кути відповідають ing рівні, Однак в деяких випадках можна зробити висновок, що два трикутники є конгруентними, з лише частковою інформацією про їхні сторони та кути.

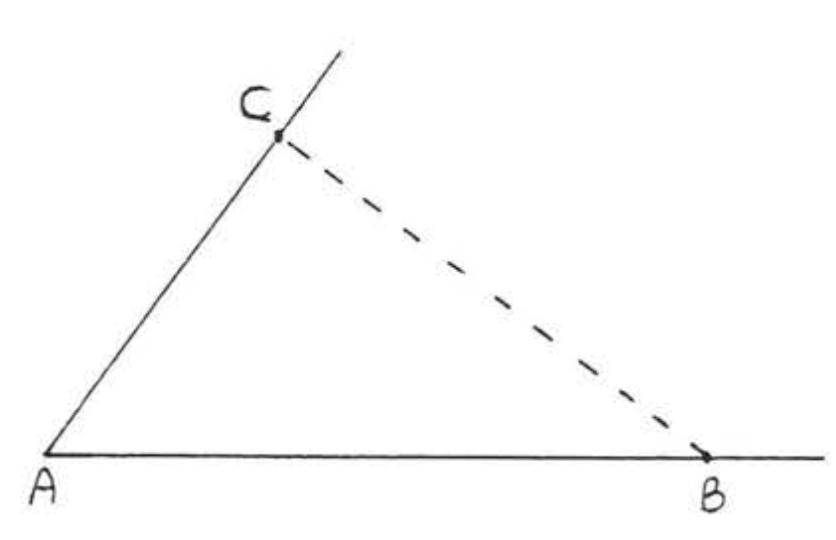
Припустимо, нам кажуть, що$\triangle ABC$ має$\angle A = 53^{\circ}$,$AB = 5$ дюйми та$AC = 3$ дюйми. Звернемося до ескізу$\triangle ABC$. Спочатку малюємо$53^{\circ}$ кутоміром кут і маркуємо його$\angle A$. Використовуючи лінійку, ми знаходимо точку 5 дюймів від вершини на одній стороні кута і позначити її$B$, На іншій стороні кута, ми знаходимо точку 3 дюймів від вершини і позначити її$C$, Див. Рисунок$\PageIndex{1}$, Зараз є тільки один спосіб для нас, щоб завершити наш ескіз$\triangle ABC$, і тобто з'єднати точки$B$ і$C$ з відрізком лінії, Ми могли б тепер виміряти$BC$$\angle B$, і$\angle C$ знайти інші частини трикутника.

2020-10-30 3.03.10.пнг — Малюнок$\PageIndex{1}$: Ескіз$\triangle ABC$.

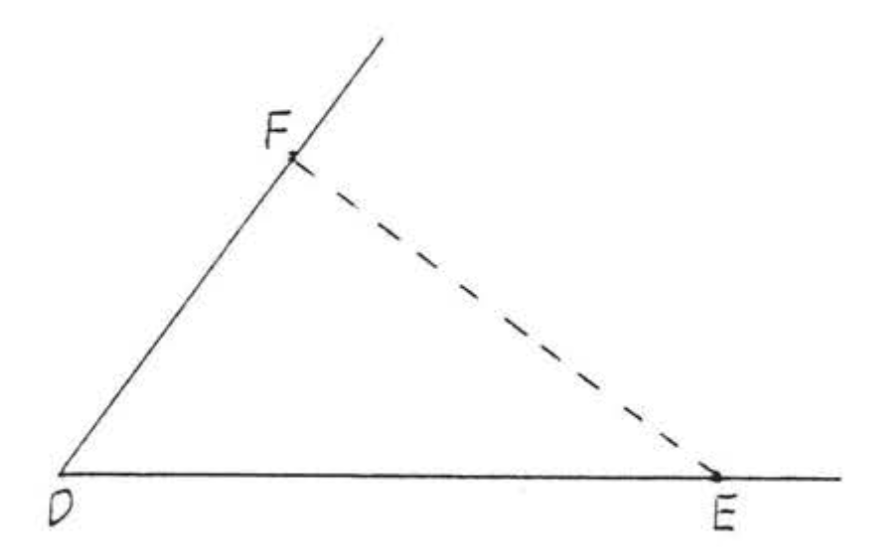
2020-10-30 3.04.09.пнг — Малюнок$\PageIndex{2}$: Ескіз$\triangle DEF$.

Припустимо, тепер$\triangle DEF$ були ще один трикутник$\angle D = 53^{\circ}$, з,$DE = 5$ дюйми, і$DF = 3$ дюйми. Ми могли б ескіз так$\triangle DEF$ само, як ми зробили$\triangle ABC$, а потім виміряти$EF$$\angle E$, і$\angle F$ (Рисунок$\PageIndex{2}$). Зрозуміло, що ми повинні мати$BC = EF$$\angle B = \angle E$, і$\angle C = \angle F$ тому обидва трикутника були намальовані абсолютно однаково. Тому$\triangle ABC \cong \triangle DEF$.

В$\triangle ABC$, ми говоримо, що$\angle A$ це кут, включений між сторонами$AB$ і$AC$.
В$\triangle DEF$, ми говоримо, що$\angle D$ це кут, включений між сторонами$DE$ і$DF$.

Наша дискусія передбачає наступну теорему:

Теорема$\PageIndex{1}$ (SAS or Side-Angle-Side Theorem)

Два трикутника є конгруентними, якщо дві сторони і включений кут однієї рівні відповідно двом сторонам, а включений кут інший,

На малюнку$\PageIndex{1}$ and $\PageIndex{2}$, $\triangle ABC \cong \triangle DEF$ because $AB, AC$, and $\angle A$ are equal respectively to $DE, DF$ and $\angle D$.

Іноді ми скорочуємо теорему$\PageIndex{1}$, просто пишемо$SAS = SAS$.

Приклад$\PageIndex{1}$

У$\triangle PQR$ назві кут, включений між сторонами

$PQ$і$QR$,
$PQ$і$PR$,
$PR$і$QR$,

Рішення

Зверніть увагу, що включений кут називається літерою, яка є спільною для обох сторін, Для (1) буква$Q$ "" є загальною для$PQ$$QR$ і тому$\angle Q$ включена між сторонами$PQ$ і$QR$. Аналогічно для (2) і (3).

Відповідь: (1)$\angle Q$, (2)$\angle P$, (3)$\angle R$.

Приклад$\PageIndex{2}$

Для двох трикутників на схемі

перерахуйте дві сторони і включений кут кожного трикутника, які відповідно рівні, використовуючи інфонацію, наведену на діаграмі,
написати заяву про конгруентність,

і (3) знайти,$x$ ідентифікуючи пару відповідних сторін конгруентних трикутників.

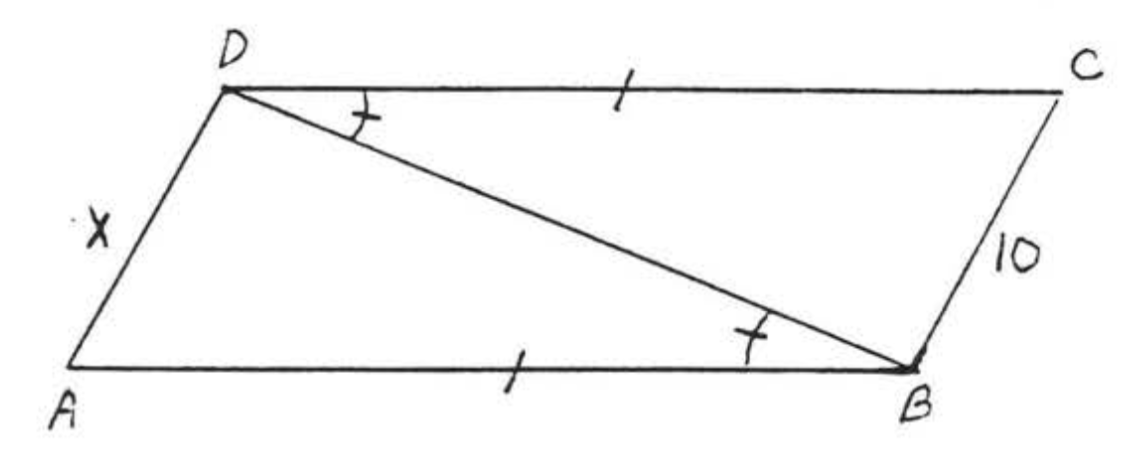
$2020-10-30 3.17.42.png$

Рішення

(1) Кути і сторони, які позначені однаково на діаграмі, приймаються рівними, Так$\angle B$ в$\triangle ABD$ дорівнює$\angle D$ в$\triangle BCD$. Тому «$B$" відповідає "$D$. У нас теж є$AB = CD$. Тому "$A$" має відповідати "$C$». Таким чином, якщо трикутники конгруентні, відповідність повинна бути

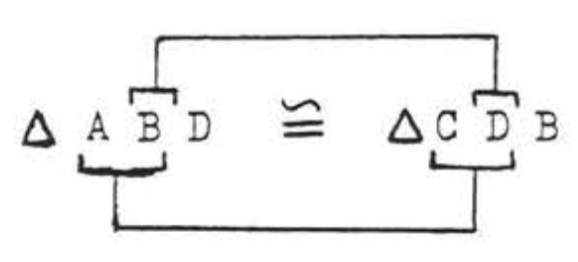
$2020-10-30 3.21.21.png$

Нарешті,$BD$ (так само, як$DB$) є стороною, спільною для обох трикутників, підсумовуючи,

$\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ABD}} & \ & {\underline{\triangle CDB}} & \ & {} \\ {\text{Side}} & \ & {AB} & = & {CD} & \ & {\text{(marked = in diagram)}} \\ {\text{Included Angle}} & \ & {\angle B} & = & {\angle D} & \ & {\text{(marked = in diagram)}} \\ {\text{Side}} & \ & {BD} & = & {DB} & \ & {\text{(common side)}} \end{array}$

(2)$\triangle ABD \cong \triangle CDB$ через теорему SAS ($SAS = SAS$).

(3)$x = AD = CB = 10$ тому що$AD$ і$CB$ є відповідними сторонами (перша та третя літери в заяві про конгруентність) a.~d відповідні сторони конгруентних трикутників рівні.

Відповідь:

(1)$AB$,$\angle B$,$BD$ з$\triangle ABD = CD$$\angle D$,$DB$ оф$\triangle CDB$.

(2)$\triangle ABD \cong \triangle CDB$.

(3)$x = AD = CB = 10$.

Приклад$\PageIndex{3}$

Для двох трикутників на схемі

перерахуйте дві сторони і включений кут кожного трикутника, які відповідно рівні, використовуючи інформацію, наведену на схемі.
написати заяву про конгруентність, і
знайти$x$ і$y$ шляхом ідентифікації пари відповідних сторін конгруентних трикутників.

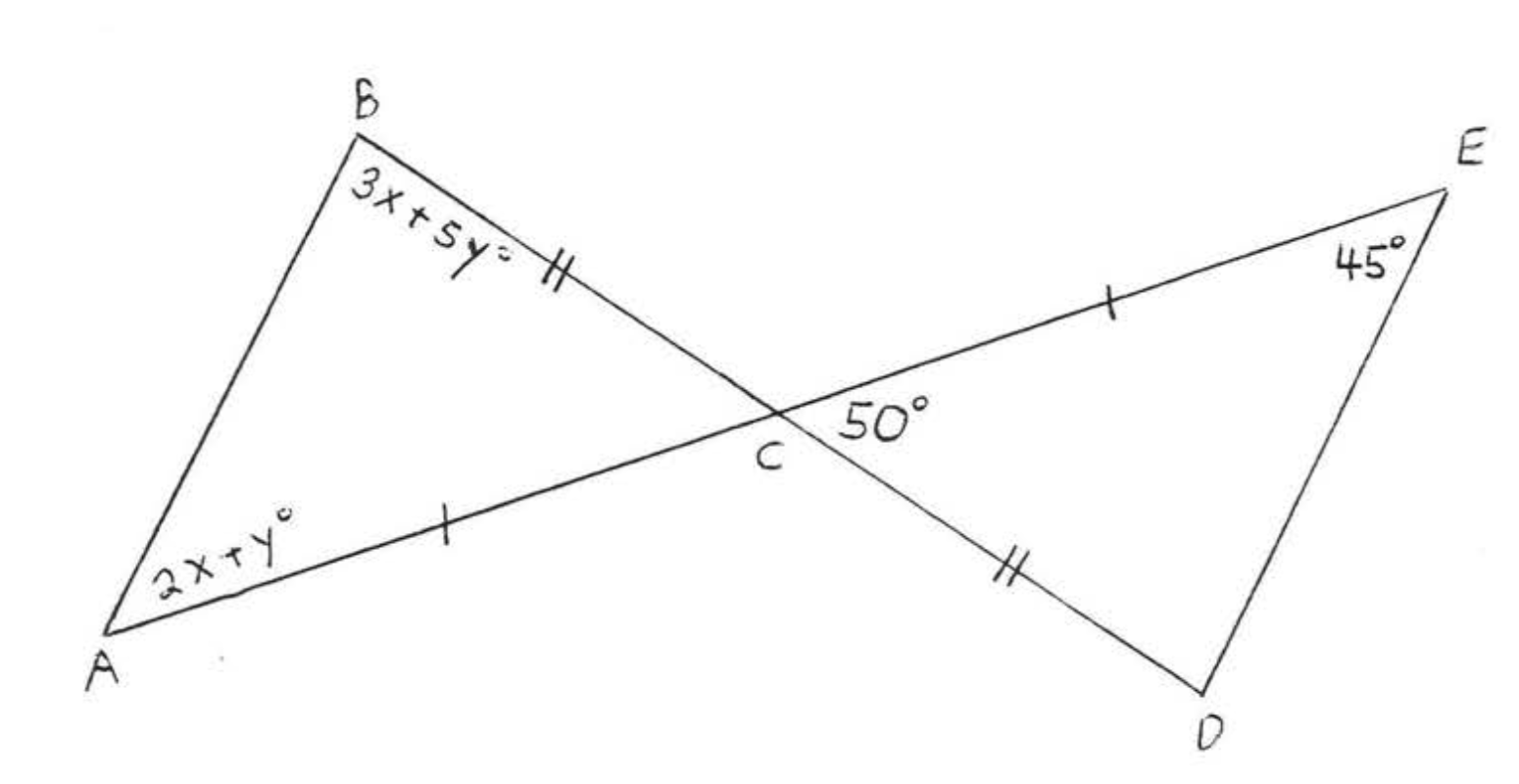
$2020-10-30 3.34.32.png$

Рішення

(1)$AC = CE$ і$BC = CD$ тому, що вони марні! ,; :ed так само. Ми також знаємо, що$\angle ACB = \angle ECD = 50^{\circ}$ тому, що вертикальні кути рівні. Тому "$C$" in$\triangle ABC$ відповідає "$C$" в$\triangle CDE$. Оскільки$AC = CE$ ми повинні мати, що$A$ "" in$\triangle ABC$ відповідає "$E$" в$\triangle CDE$. Таким чином, якщо трикутники конгруентні, відповідність повинна бути

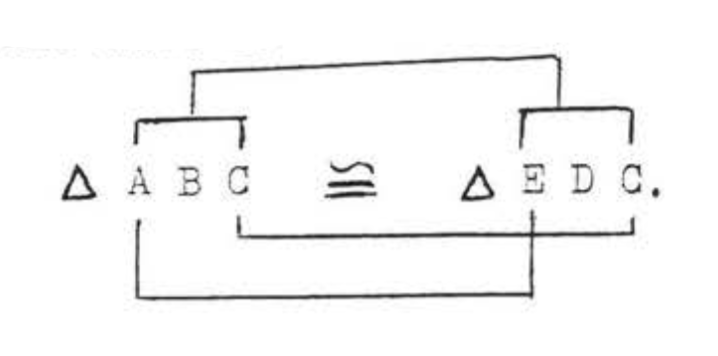
$2020-10-30 3.41.57.png$

Підсумовуємо:

$\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ABC}} & \ & {\underline{\triangle EDC}} & \ & {} \\ {\text{Side}} & \ & {AC} & = & {EC} & \ & {\text{(marked = in diagram)}} \\ {\text{Included Angle}} & \ & {\angle ACB} & = & {\angle ECD} & \ & {\text{(vertical angles are =)}} \\ {\text{Side}} & \ & {BC} & = & {DC} & \ & {\text{(marked = in diagram)}} \end{array}$

(2)$\triangle ABC \cong \triangle EDC$ через теорему SAS. ($SAS = SAS$)

(3)$\angle A = \angle E$ і$\angle B = \angle D$ тому, що вони є корелями:9onding кути конгруентних трикутників. $\angle D = 85^{\circ}$тому що сума кутів$\triangle EDC$ повинна бути$180^{\circ}$. ($\angle D = 180^{\circ} - (50^{\circ} + 45^{\circ}) = 180^{\circ} - 95^{\circ} = 85^{\circ}$). Отримаємо систему з двох рівнянь в двох невідомих$x$ і$y$:

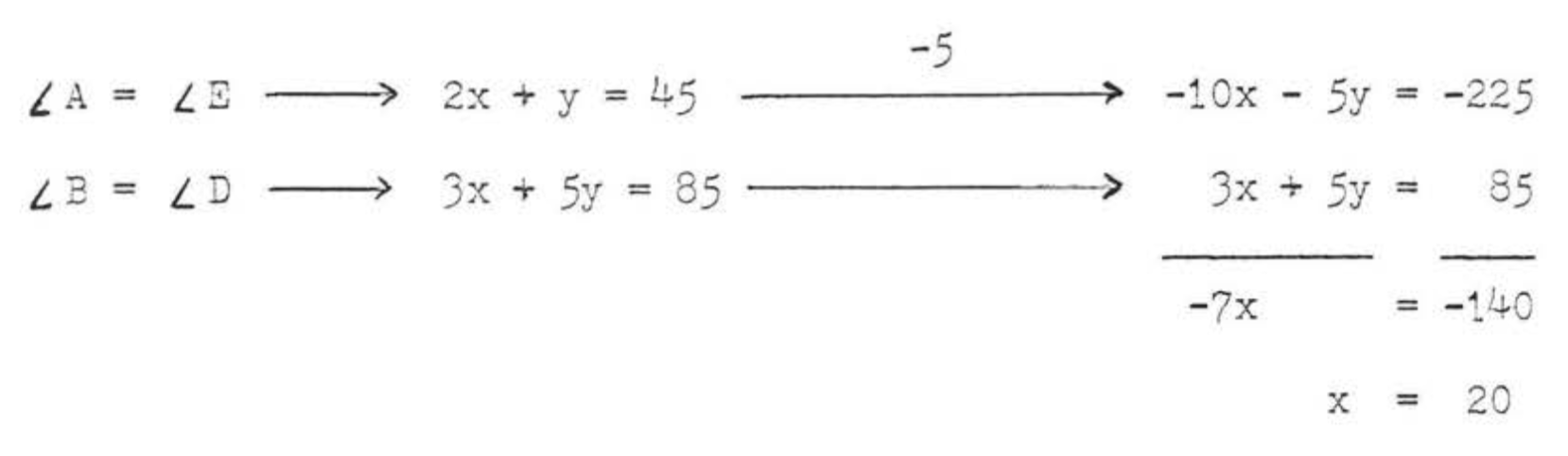
$2020-10-30 3.46.35.png$

Підставляючи$x$ в першому вихідному рівнянні,

\[\begin{array} {rcl} {2x + y} & = & {45} \\ {2(20) + y} & = & {45} \\ {40 + y} & = & {45} \\ {y} & = & {45- 40} \\ {y} & = & {5} \end{array}\]

Перевірка:

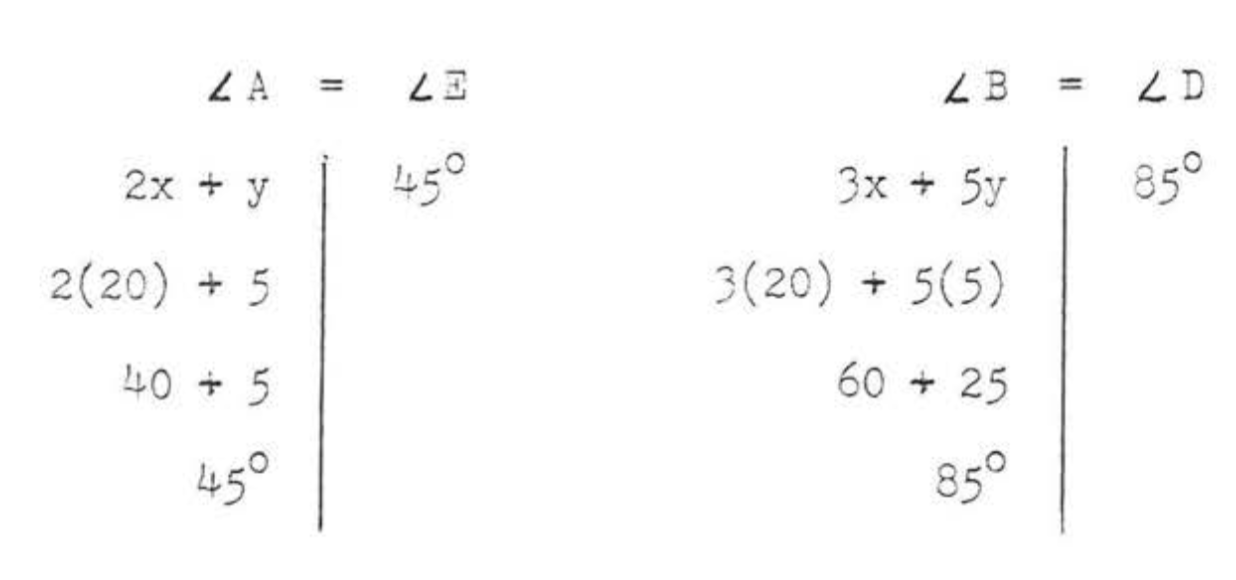
$2020-10-30 3.50.00.PNG$

Відповідь:

$AC$,$\angle ACB$,$BC$ з$\triangle ABC$ =$EC, \angle ECD, DC$ з$\triangle EDC$.
$\triangle ABC \cong \triangle EDC$.
$x = 20, y = 5$.

Приклад$\PageIndex{4}$

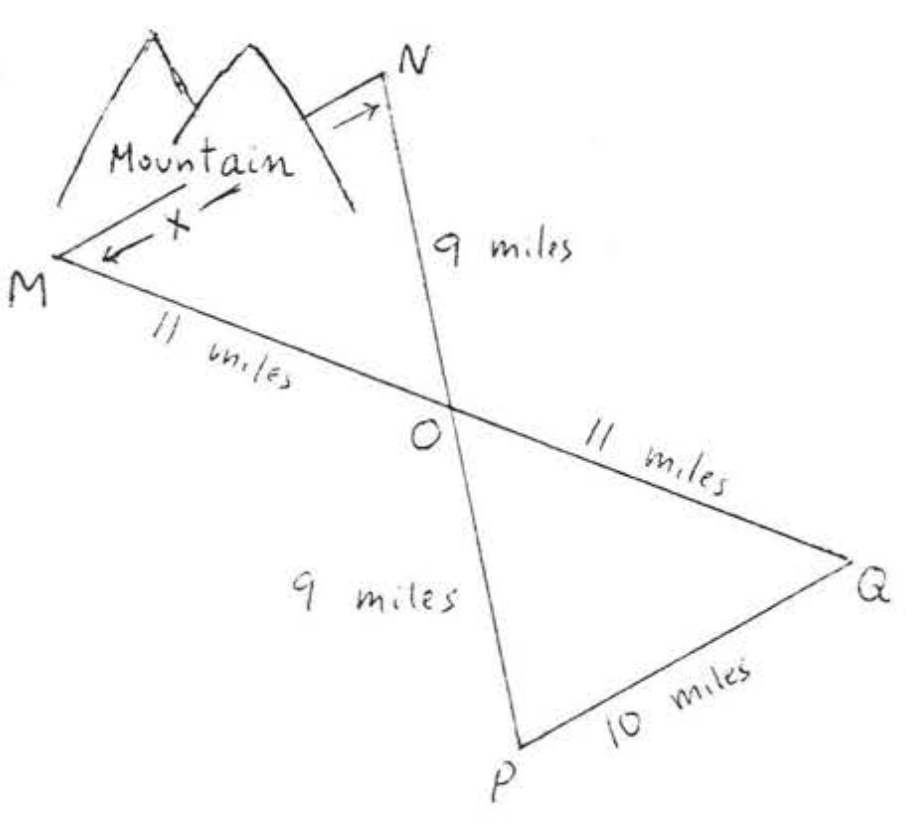
Наступна процедура була використана для вимірювання d.istance AB через ставок: З точки$C$,$AC$ і$BC$ були виміряні і виявилися 80 і 100 футів відповідно. Потім$AC$ був продовжений до$E$ так, що$AC = CE$ і$BC$ був продовжений$D$ так, що$BC = CD$. Нарешті,$DE$ ми виявили, що 110 футів.

Напишіть заяву про конгруентність.
Дайте привід для (1).
Знайти$AB$.

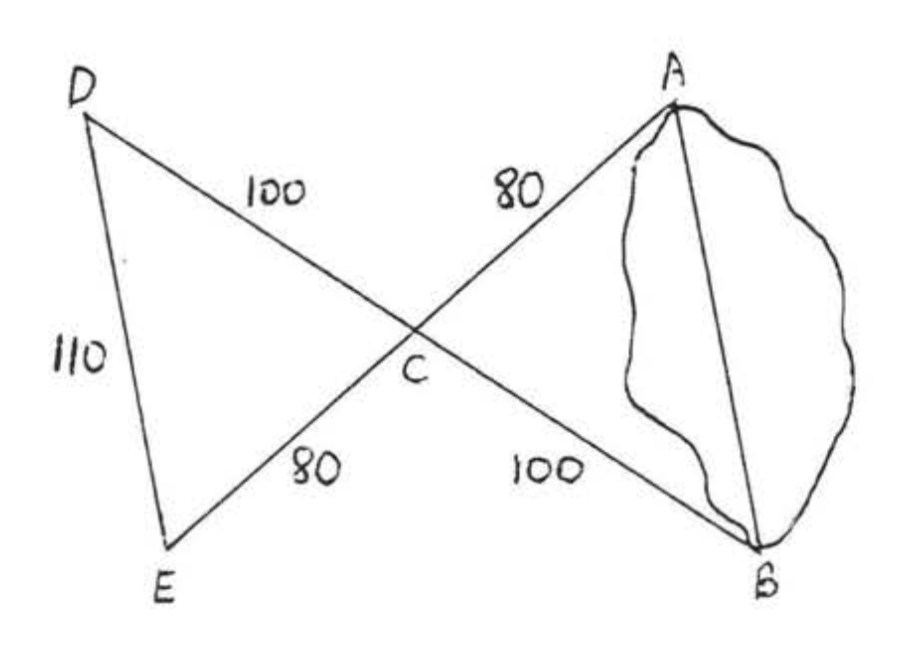
$2020-10-30 3.55.21.png$

Рішення

(1)$\angle ACB = \angle ECD$ тому що вертикальні кути рівні. Тому «$C$s» відповідають,$AC = EC$ тому$A$ повинні відповідати$E$. У нас є

$2020-10-30 3.56.25.png$

(2)$SAS = SAS$. $AC$Сторони$BC$, і$C$ включений$ABC$ кут дорівнює відповідно$EC, DC$, і$C$ включений кут$\angle EDC$.

(3)$AB = ED$ тому що вони є відповідними сторонами конгруентних трикутників, Оскільки$ED = 110$,$AB = 110$.

Відповідь

(1)$\triangle ABC \cong \triangle EDC$.

(2)$SAS = SAS$:$AC$,$\angle C$,$BC$ з$\triangle ABC = EC$,$\angle C$,$DC$ з$\triangle EDC$.

(3)$AB = 110 feet$.

Історична записка

Теорема SAS - це пропозиція 4 в елементах Евкліда. І наше обговорення, і доказ Сукліта теореми SAS явно використовують наступний принцип: Якщо геометрична конструкція повторюється в іншому місці (або те, що становить те ж саме, «переміщено» в інше місце), то розмір і форма фігури залишаються незмінними, Є докази того, що Евклід використовував цей принцип неохоче, і багато математиків з тих пір ставлять під сумнів його використання в офіційних доказах, Вони вважають, що це робить занадто сильним припущення про природу фізичного простору і є нижчою формою геометричних міркувань. Бертран Рассел (1872 - 1970), наприклад, припустив, що нам було б краще припустити теорему SAS як постулат, Це насправді зроблено в системі аксіом для евклідової геометрії, розробленої Девідом Гільбертом (1862 - 1943), система, яка отримала велику користь у сучасних математиків. Гільберт був провідним експонентом «формалістської школи», яка прагнула виявити, які саме припущення лежать в основі кожної галузі математики і усунути всі логічні неясності, система Гільберта, однак, занадто формальна для вступного курсу з геометрії,

Проблеми

1 - 4. Для кожного з наступних (1) намалюйте трикутник з двома сторонами та включеним кутом і (2) виміряйте решту сторони та кути:

1. $AB = 2$дюйми,$AC = 1$ дюйми,$\angle A = 60^{\circ}$.

2. $DE = 2$дюйми,$DF = 1$ дюйми,$\angle D = 60^{\circ}$.

3. $AB = 2$дюйми,$AC = 3$ дюйми,$\angle A = 40^{\circ}$.

4. $DE = 2$дюйми,$DF = 3$ дюйми,$\angle D = 40^{\circ}$.

5 - 8. Назвіть кут, включений між сторонами

5. $AB$і$BC$ в$\triangle ABC$.

6. $XY$і$YZ$ в$\triangle XYZ$.

7. $DE$і$DF$ в$\triangle DEF$.

8. $RS$і$TS$ в$\triangle RST$.

9 - 22. Для кожного з наступних.

(1) перерахуйте дві сторони та включений кут кожного трикутника, які відповідно рівні, використовуючи інформацію, наведену на діаграмі,

(2) написати заяву про конгруентність,

(3) знайти$x$, або$x$ і$y$.

Припустимо, що кути або сторони, позначені таким же чином, рівні.

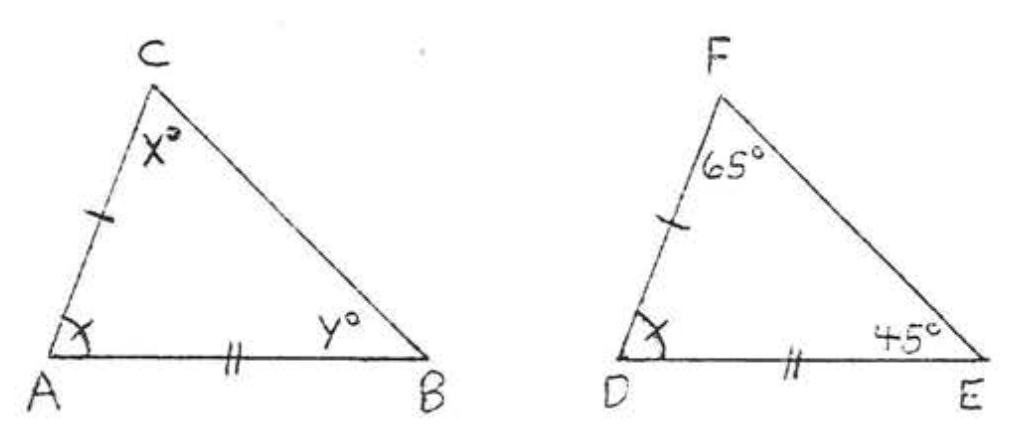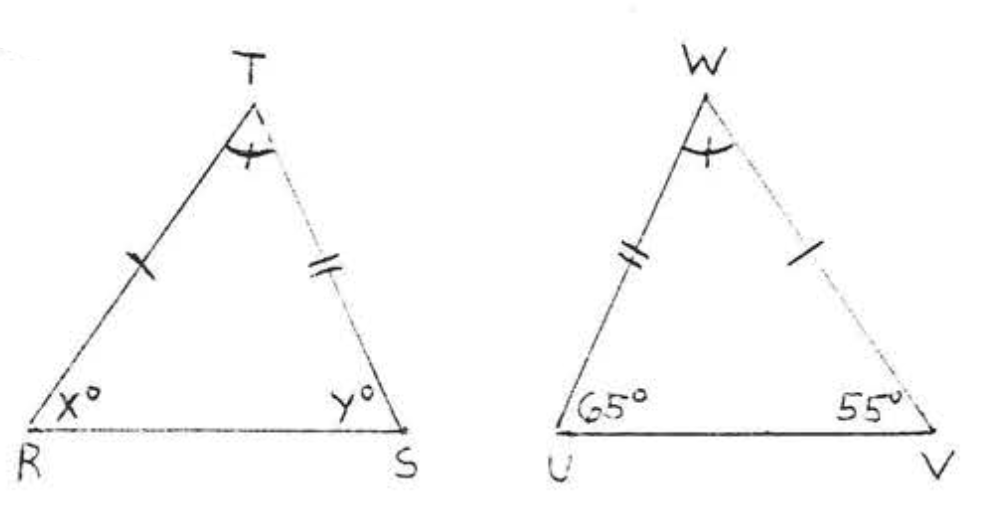
9. $Знімок екрана 2020-10-30 у 4.15.31 PM.png$ 10. $Знімок екрана 2020-10-30 у 4.15.53 PM.png$

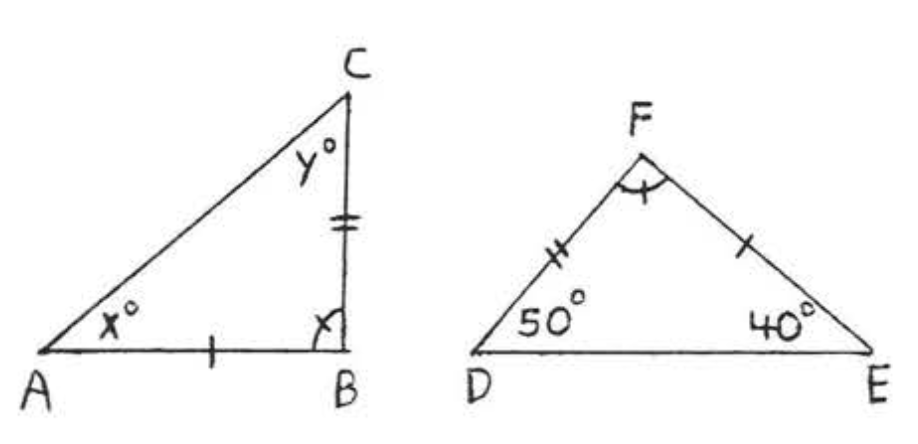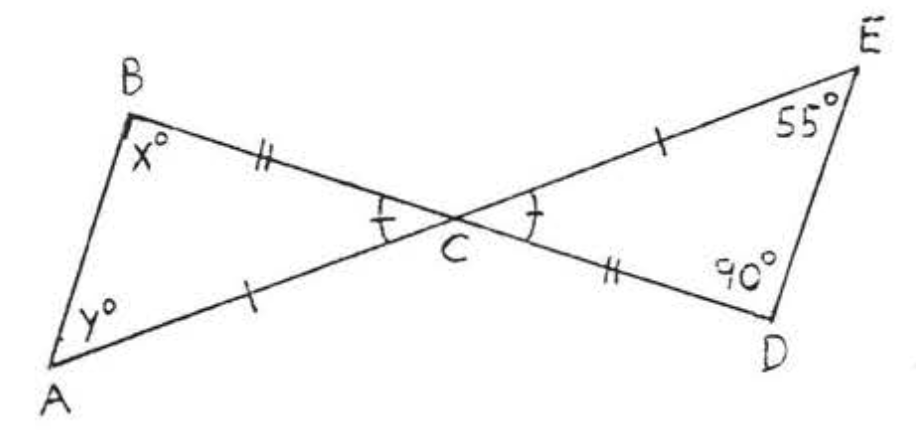
11. $Знімок екрана 2020-10-30 у 4.16.11 PM.png$ 12. $Знімок екрана 2020-10-30 у 4.16.32 PM.png$

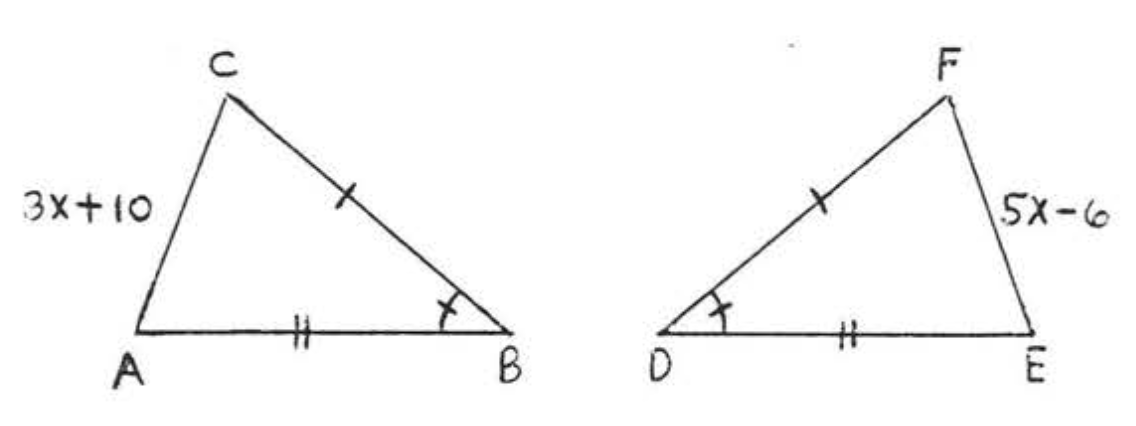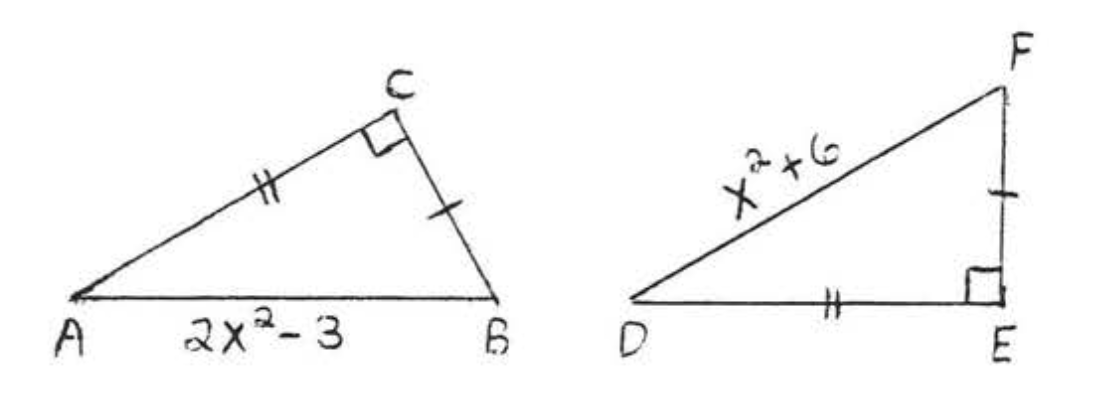
13. $Знімок екрана 2020-10-30 у 4.16.58 PM.png$ 14. $Знімок екрана 2020-10-30 у 4.17.13 PM.png$

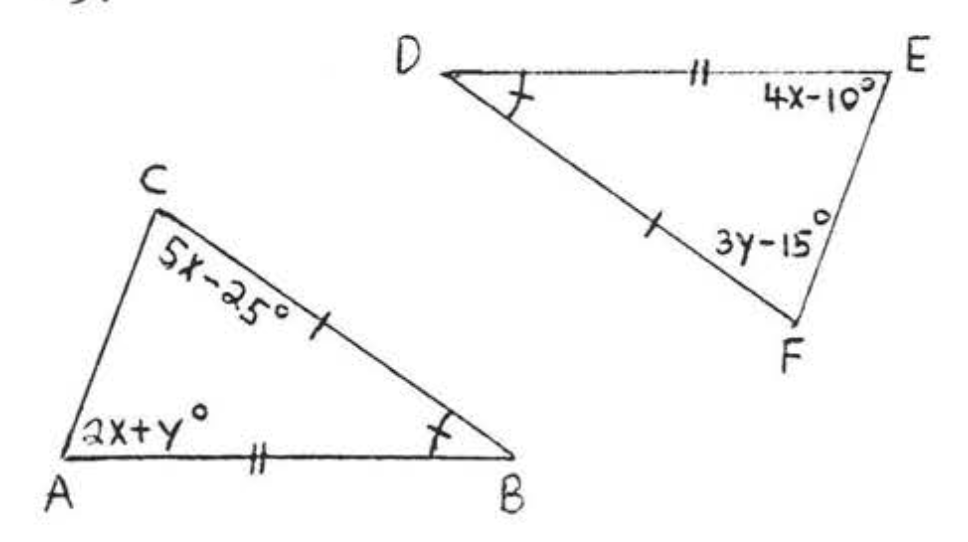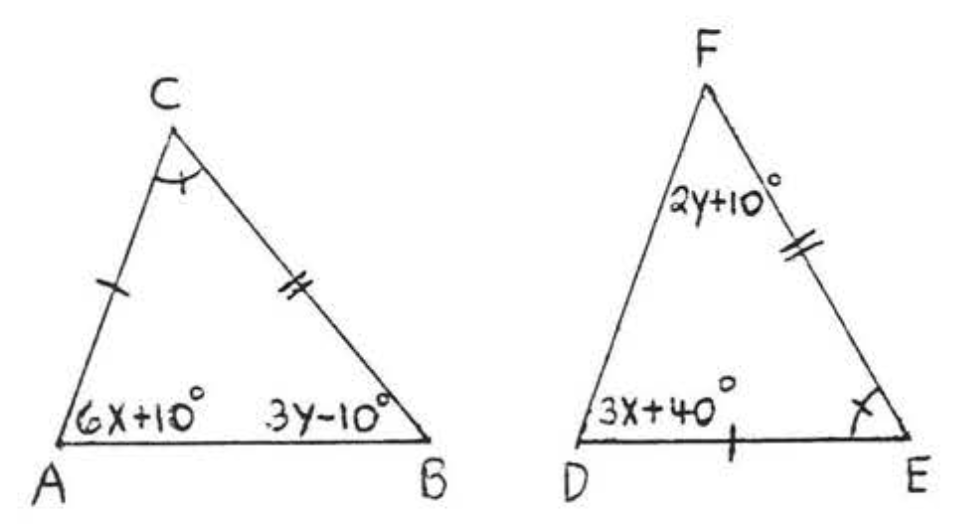
15. $Знімок екрана 2020-10-30 у 4.17.29 PM.png$ 16. $Знімок екрана 2020-10-30 у 4.17.50 PM.png$

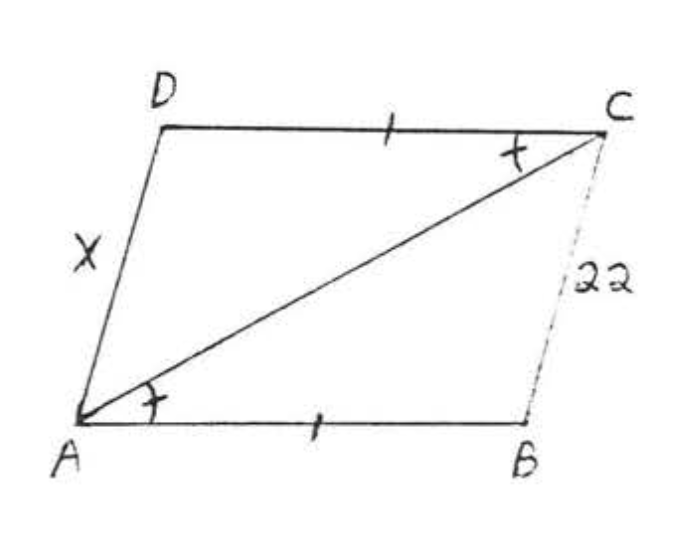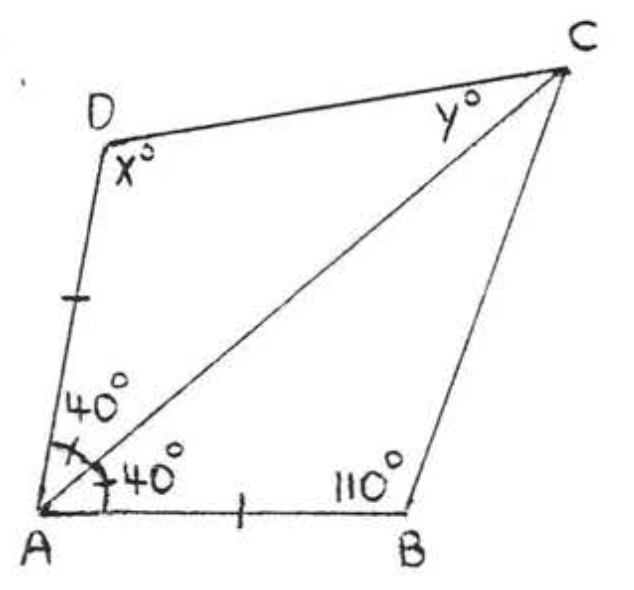
17. $Знімок екрана 2020-10-30 у 4.18.18 PM.png$ 18. $Знімок екрана 2020-10-30 у 4.18.32 PM.png$

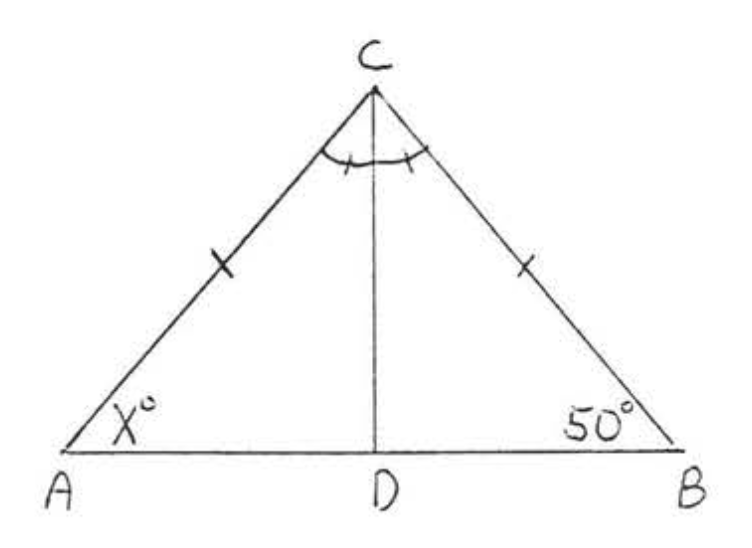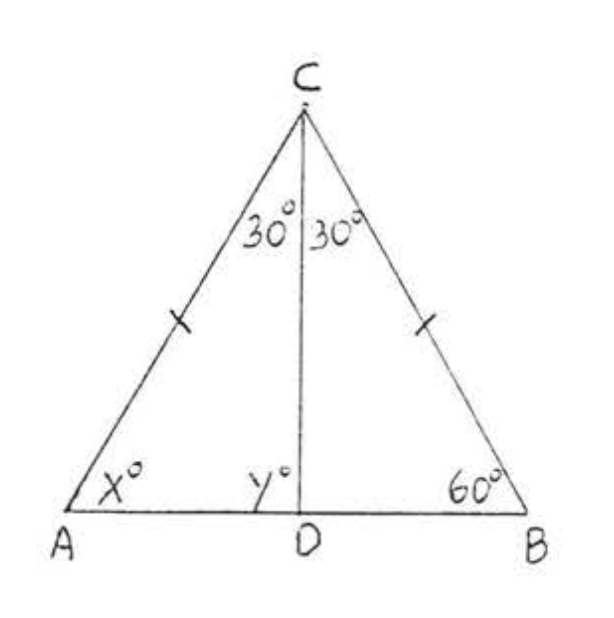
19. $Знімок екрана 2020-10-30 у 4.18.53 PM.png$ 20. $Знімок екрана 2020-10-30 у 4.19.05 PM.png$

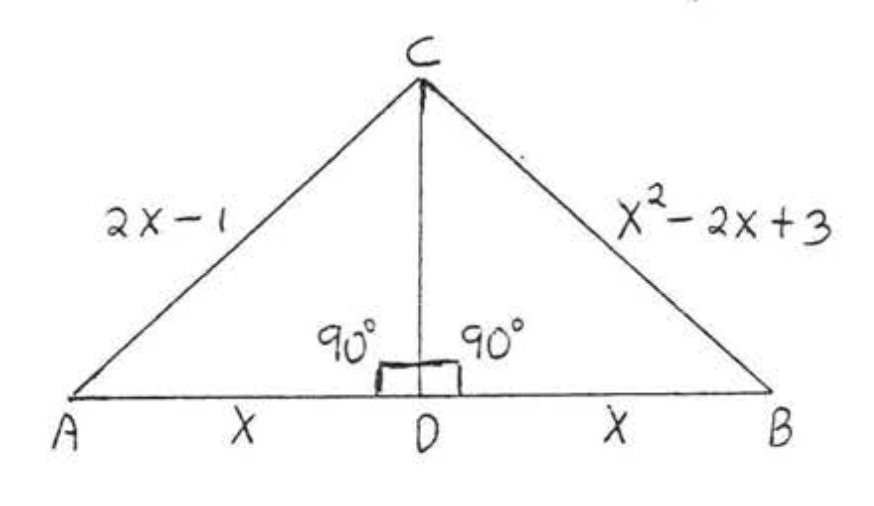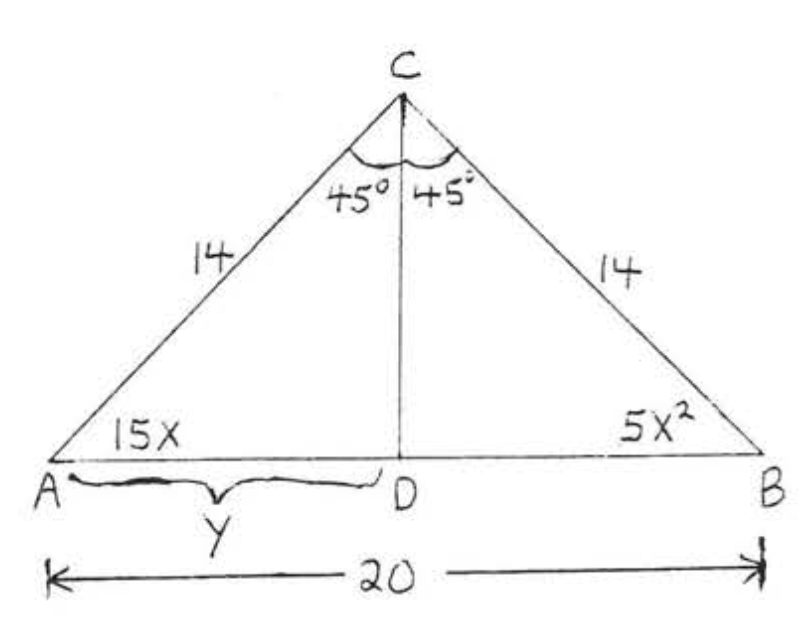
21. $Знімок екрана 2020-10-30 у 4.19.25 PM.png$ 22. $Знімок екрана 2020-10-30 у 4.19.41 PM.png$

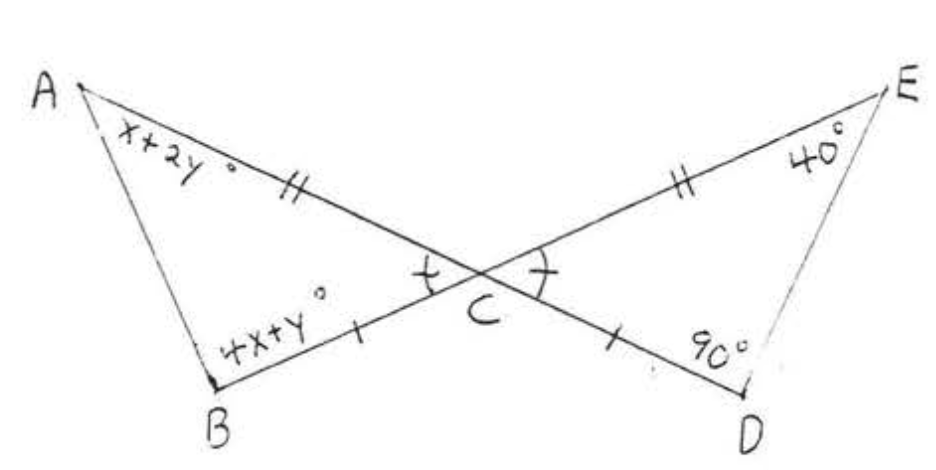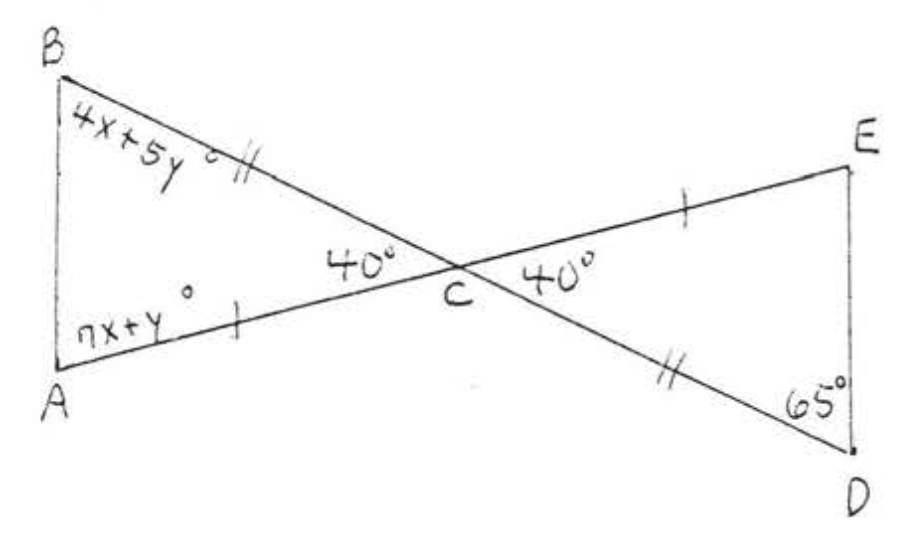
23. $Знімок екрана 2020-10-30 у 4.20.09 PM.png$ 24. $Знімок екрана 2020-10-30 у 4.20.34 PM.png$

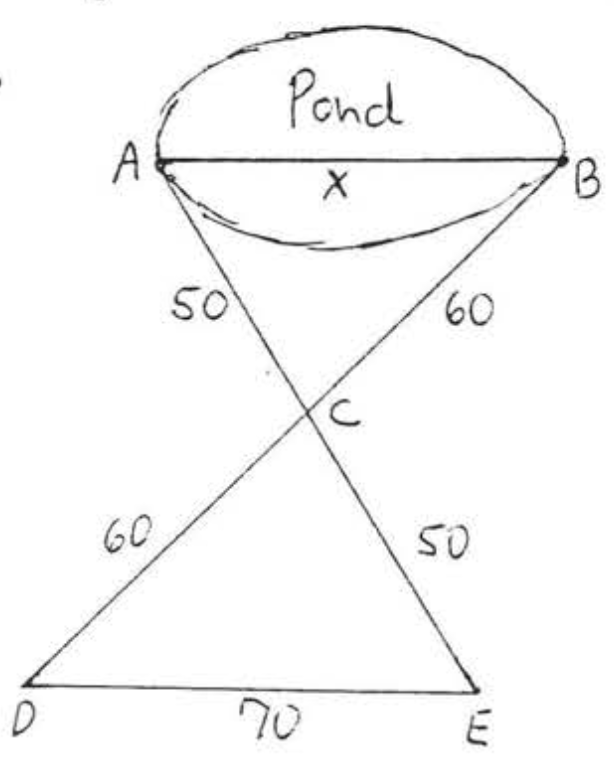25. $Знімок екрана 2020-10-30 у 4.21.03 PM.png$ 26. $Знімок екрана 2020-10-30 у 4.21.22 PM.png$

Теорема\(\PageIndex{1}\) (SAS or Side-Angle-Side Theorem)

Приклад\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\)

Історична записка

Проблеми