2.3: Теореми ASA та AAS
- Page ID
- 58834
У цьому розділі ми розглянемо ще два випадки, коли можна зробити висновок, що трикутники збігаються тільки з частковою інформацією про їх сторонам і кутах,
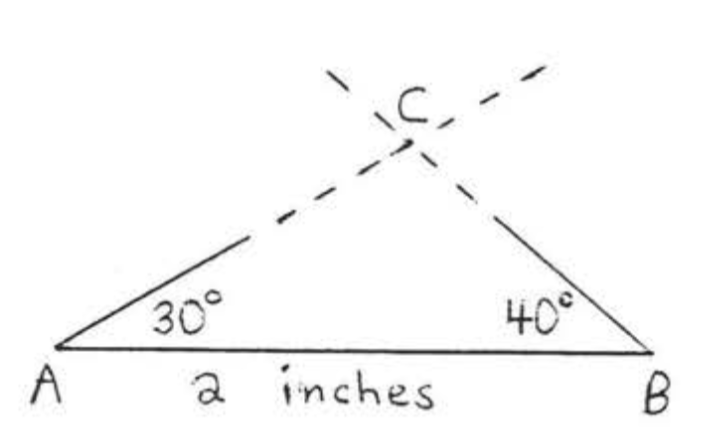
Припустимо, нам кажуть, що\(\triangle ABC\) має\(\angle A = 30^{\circ}, \angle B = 40^{\circ}\), і\(AB =\) 2 дюйма. Давайте спробуємо зробити ескіз\(\triangle ABC\). Спочатку малюємо відрізок лінії в 2 дюйма і маркуємо його\(AB\), транспортиром малюємо кут\(30^{\circ}\) під\(A\) і кут\(40^{\circ}\) в\(B\) (рис.\(\PageIndex{1}\)). Продовжуємо лінії формування\(\angle A\) і\(\angle B\) поки вони не зустрінуться в\(C\). Тепер ми могли б виміряти\(AC, BC\), і\(\angle C\) знайти залишилися частини трикутника.
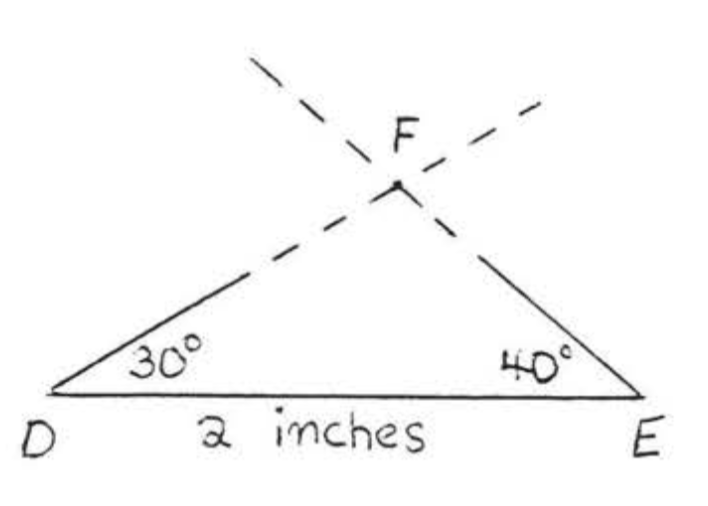
\(\triangle DEF\)Дозволяти бути ще один трикутник\(\angle D = 30^{\circ}\), з\(\angle E = 40^{\circ}\),, і\(DE =\) 2 дюйми. Ми могли б ескіз так\(\triangle DEF\) само, як ми зробили\(\triangle ABC\), а потім виміряти\(DF, EF\), і\(\angle F\) (рис.\(\PageIndex{2}\)). Зрозуміло, що ми повинні мати\(AC = DF\)\(BC = EF\), і\(\angle C = \angle F\), тому що обидва трикутника були намальовані точно так само, тому\(\triangle ABC \cong \triangle DEF\).
У\(\triangle ABC\) ми говоримо, що\(AB\) це сторона включена між\(\angle A\) і\(\angle B\). У\(\triangle DEF\) ми б сказали, що DE - це сторона, включена між\(\angle D\) і\(\angle E\).
Наша дискусія передбачає наступну теорему:
Два трикутника є конгруентними, якщо два кути і включена сторона одного дорівнюють відповідно двом кутам і включеній стороні іншого.
На малюнку\(\PageIndex{1}\) and \(\PageIndex{2}\), \(\triangle ABC \cong \triangle DEF\) because \(\angle A, \angle B\), and \(AB\) are equal respectively to \(\angle D\), \(\angle E\), and \(DE\).
Ми іноді скорочуємо теорему\(\PageIndex{1}\) by simply writing \(ASA = ASA\).
В\(\triangle PQR\), назвіть сторону, що входить між
- \(\angle P\)і\(\angle Q\).
- \(\angle P\)і\(\angle R\).
- \(\angle Q\)і\(\angle R\).
Рішення
Зверніть увагу, що включена сторона називається двома літерами, що представляють кожен з кутів. Тому для (1) сторона, що входить між\(\angle P\) і,\(\angle Q\) називається буквами\(P\) і\(Q\) — тобто стороною\(PQ\). Аналогічно для (2) і (3).
Відповідь: (1)\(PQ\), (2)\(PR\), (3)\(QR\).
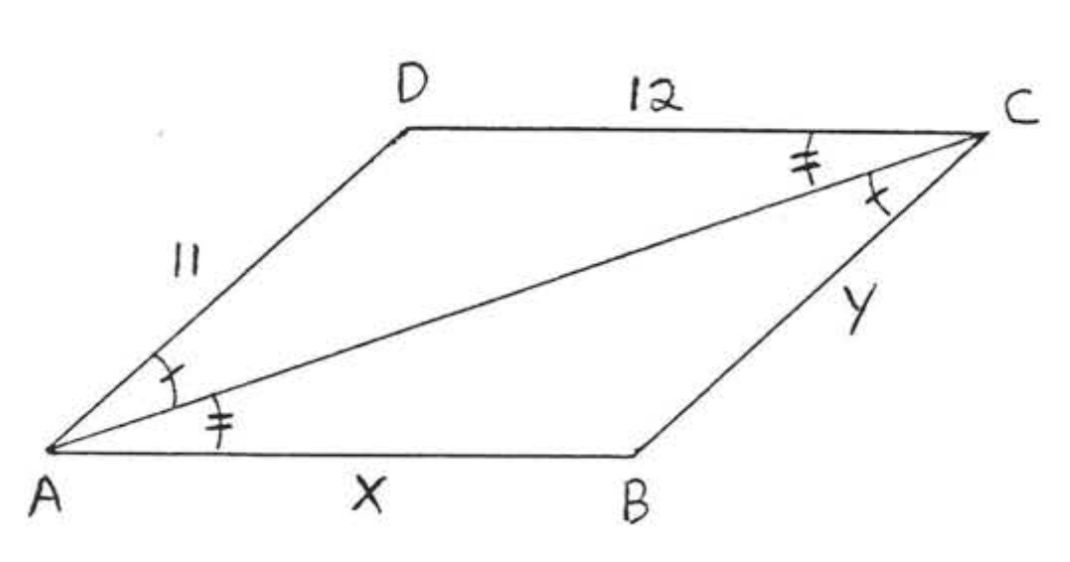
Для двох трикутників на схемі
- написати заяву про конгруентність,
- дати привід для (1),
- знайти\(x\) і\(y\).
Рішення
(1) Від діаграми\(\angle A\) в\(\triangle ABC\) дорівнює\(\angle C\) в\(\triangle ADC\). Тому «\(A\)" відповідає "\(C\)». Також\(\angle C\) в\(\triangle ABC\) дорівнює\(\angle A\) в\(\triangle ADC\). Так що\(C\) "" відповідає "\(A\)». У нас є
(2)\(\angle A, \angle C\), і включена сторона\(AC\) дорівнює відповідно\(\angle C\)\(\angle A\), і включена\(CA\) сторона\(\triangle CDA\).\(\triangle ABC\) (\(AC = CA\)Тому що вони просто різні імена для ідентичного сегмента лінії, Ми іноді говоримо\(AC = CA\) через ідентичність.) Тому\(\triangle ABC \cong \triangle CDA\) через теорему ASA (\(ASA = ASA\)).
Резюме:
\(\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ABC}} & \ & {\underline{\triangle CDA}} & \ & {} \\ {\text{Angle}} & \ & {\angle BAC} & = & {\angle DCA} & \ & {\text{(marked = in diagram)}} \\ {\text{Included Side}} & \ & {AC} & = & {CA} & \ & {\text{(identity)}} \\ {\text{Angle}} & \ & {\angle BCA} & = & {\angle DAC} & \ & {\text{(marked = in diagram)}} \end{array}\)
(3)\(AB = CD\) і\(BC = DA\) тому, що вони є відповідними сторонами конгруентних трикутників. Тому\(x = AB = CD = 12\) і\(y = BC = DA = 11\).
Відповідь:
(1)\(\triangle ABC \cong \triangle CDA\).
(2). \(ASA = ASA\):\(\angle A, AC, \angle C\)\(\triangle ABC = \angle C\) оф\(CA\),\(\angle A\) оф\(\triangle CDA\).
(3)\(x = 12\),\(y = 11\).
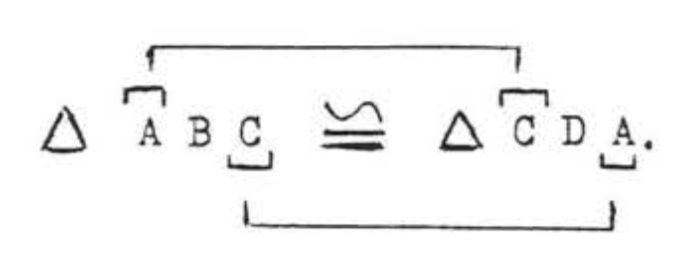
Розглянемо тепер\(\triangle ABC\) і на\(\triangle DEF\) малюнку\(\PageIndex{3}\). \(\angle A\) and \(\angle B\)
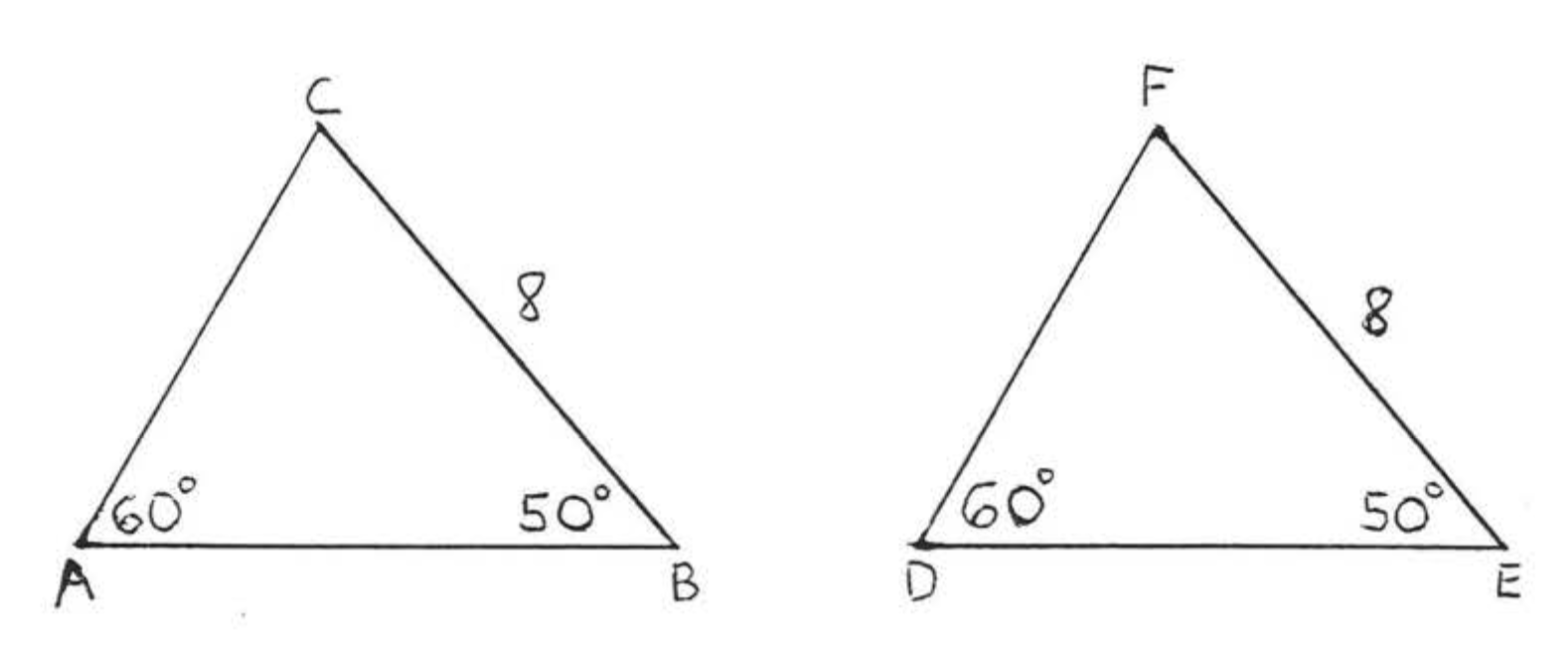
з\(\triangle ABC\) дорівнюють відповідно\(\angle D\) і\(\angle E\) з\(\triangle DEF\), але ми не маємо інформації про сторони, включені між цими кутами,\(AB\) і\(DE\), Замість цього ми знаємо, що невключена сторона BC дорівнює відповідної невключеної стороні\(EF\). Тому, як все стоїть, ми не можемо\(ASA = ASA\) зробити висновок, що трикутники є конгруентними, Однак ми можемо показати\(\angle C\) рівні,\(\angle F\) як у теоремі\(\PageIndex{3}\), section 1.5 \((\angle C = 180^{\circ} - (60^{\circ} + 50^{\circ}) = 180^{\circ} - 110^{\circ} = 70^{\circ}\) and \(\angle F = 180^{\circ} - (60^{\circ} + 50^{\circ}) = 180^{\circ} - 110^{\circ} = 70^{\circ})\). Тоді ми можемо застосувати теорему ASA до кутів Band\(C\) і їх включеної сторони\(BC\) та відповідної кути\(E\) і\(F\) з включеним бічним EF. Ці зауваження призводять нас до наступної теореми:
Два трикутника є конгруентними, якщо два кути і невключена сторона одного трикутника дорівнюють відповідно двом кутам і відповідній невключеній стороні іншого трикутника (\(AAS = AAS\)).
На малюнку\(\PageIndex{4}\), if \(\angle A = \angle D\), \(\angle B = \angle E\) and \(BC = EF\) then \(\triangle ABC \cong \triangle DEF\).
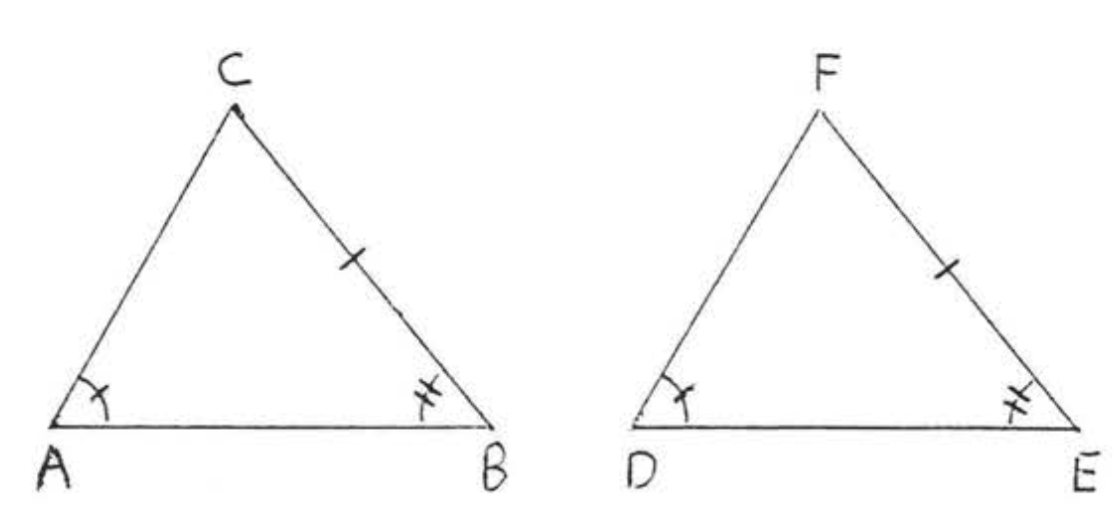
- Доказ
-
\(\angle C = 180^{\circ} - (\angle A + \angle B) = 180^{\circ} - (\angle D + \angle E) = \angle F\). Трикутники потім конгруентні,\(ASA = ASA\) застосовуючи до\(\angle B\). \(\angle C\)і\(BC\)\(\angle ABC\) і\(\angle E, \angle F\) і\(EF\) з\(\triangle DEF\).
Для двох трикутників на схемі
- написати заяву про конгруентність,
- дати привід для (1),
- знайти\(x\) і\(y\).
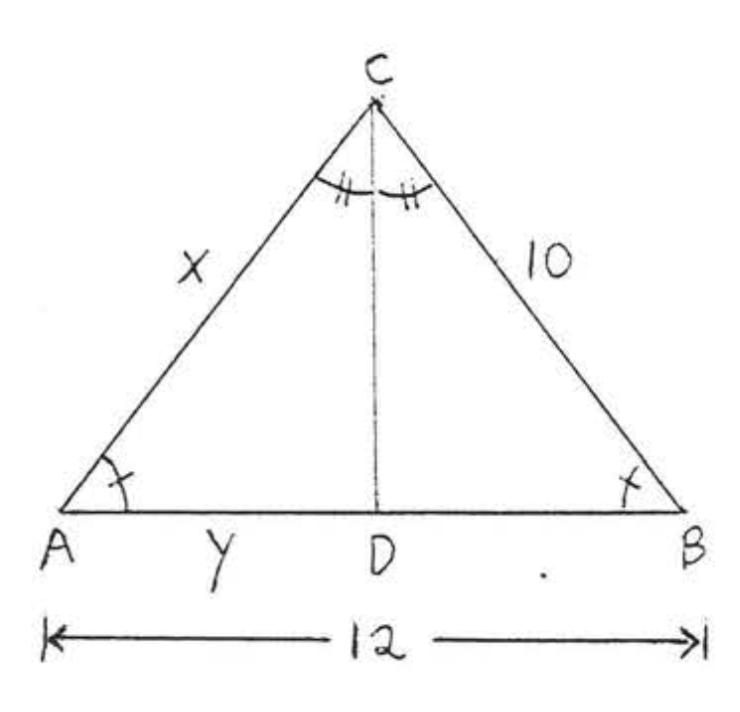
Рішення
(1)\(\triangle ACD \cong \triangle BCD\).
(2)\(AAS = AAS\) так як\(\angle A, \angle C\) і невключена сторона\(CD\) дорівнює відповідно\(\angle B, \angle C\) і не включена\(CD\) сторона\(\triangle BCD\).\(\angle ACD\)
\(\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ACD}} & \ & {\underline{\triangle BCD}} & \ & {} \\ {\text{Angle}} & \ & {\angle A} & = & {\angle B} & \ & {\text{(marked = in diagram)}} \\ {\text{Angle}} & \ & {\angle ACD} & = & {\angle BCD} & \ & {\text{(marked = in diagram)}} \\ {\text{Unincluded Side}} & \ & {CD} & = & {CD} & \ & {\text{(identity)}} \end{array}\)
(3)\(AC = BC\) і\(AD = BD\) оскільки вони є відповідними сторонами конгруентних трикутників. Тому\(x = AC = BC = 10\) і\(y = AD = BD\). Так як\(AB = AD + BD = y + y = 2y = 12\), ми повинні мати\(y = 6\).
Відповідь
(1)\(\triangle ACD \cong \triangle BCD\)
(2)\(AAS = AAS\):\(\angle A, \angle C, CD\)\(\triangle ACD = \angle B, \angle C, CD\) з\(\triangle BCD\).
(3)\(x = 10\),\(y = 6\).
Для двох трикутників на схемі
- написати заяву про конгруентність,
- дати привід для (1),
- знайти\(x\) і\(y\).
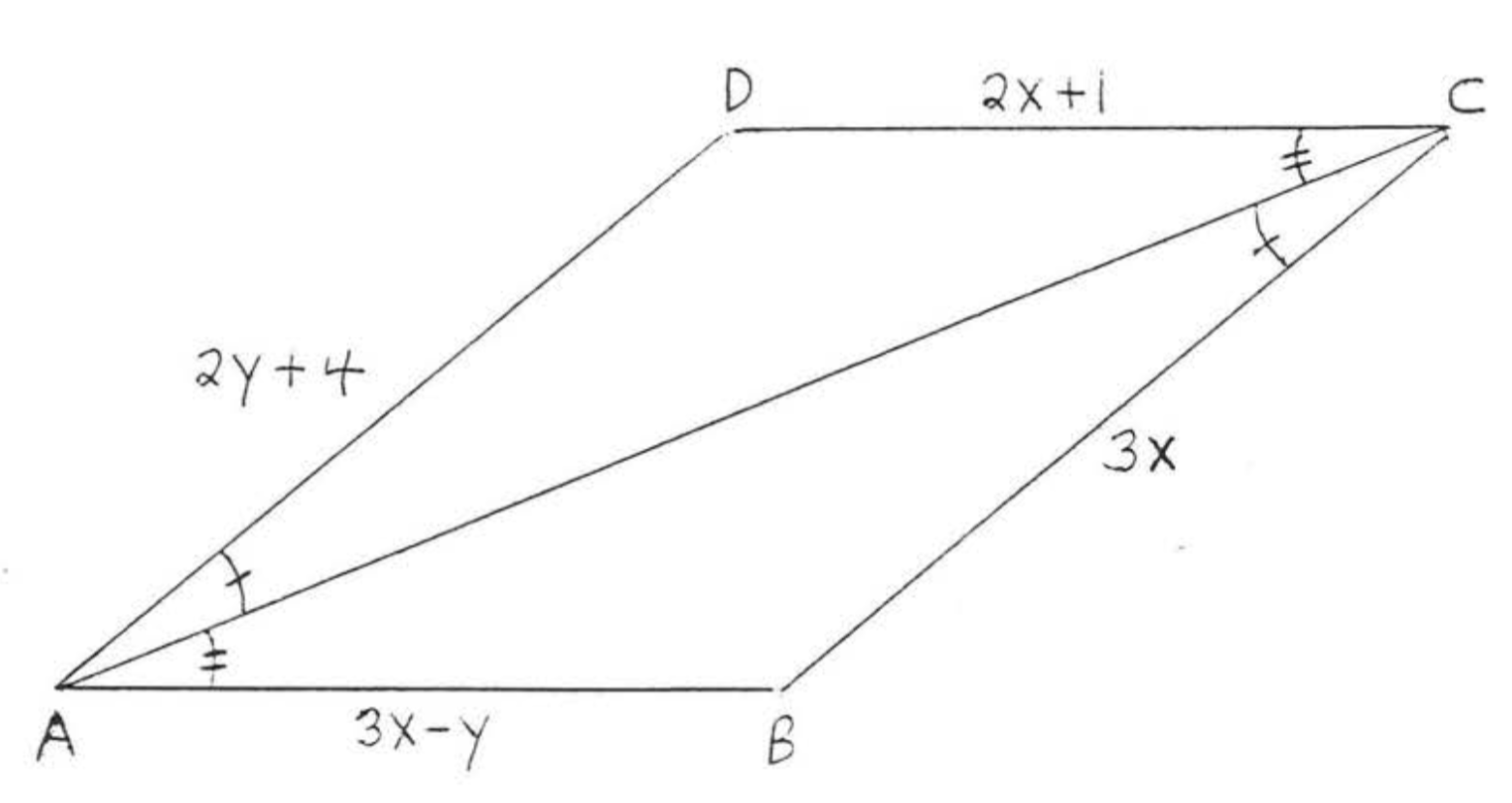
Рішення
Частина (1) і частина (2) ідентичні Прикладу\(\PageIndex{2}\).
(3):
\(\begin{array} {rcl} {AB} & = & {CD} \\ {3x - y} & = & {2x + 1} \\ {3x - 2x - y} & = & {1} \\ {x - y} & = & {1} \end{array}\)і\(\begin{array} {rcl} {BC} & = & {DA} \\ {3x} & = & {2y + 4} \\ {3x - 2y} & = & {4} \end{array}\)
Вирішуємо ці рівняння одночасно для\(x\) і\(y\):
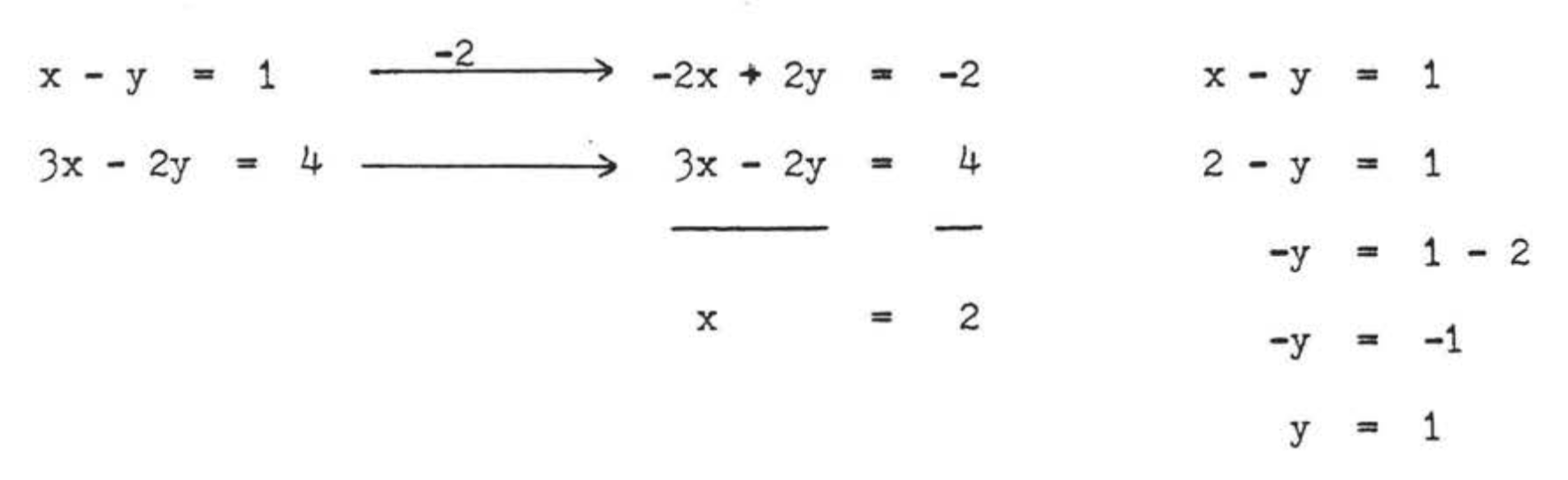
Перевірка:

Відповідь:
(1) і (2) те саме, що і приклад\(\PageIndex{2}\).
(3)\(x = 2\),\(y = 1\).
З вершини вежі Тон берег, корабель Сіс видно в море, Точка\(P\) вздовж узбережжя також видно з\(T\) так, що\(\angle PTB = \angle STB\). Якщо відстань від\(P\) підстави вежі\(B\) становить 3 милі, як далеко знаходиться корабель від точки Бон берега?
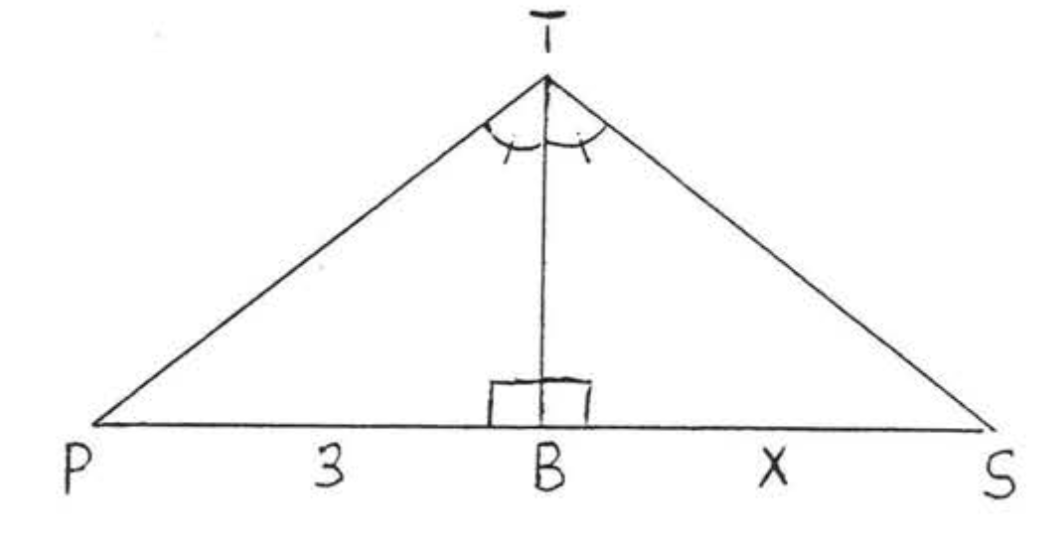
Рішення
\(\triangle PTB \cong \triangle STB\)по\(ASA = ASA\). Тому\(x = SB = FB = 3\).
Відповідь: 3 милі
Метод знаходження відстані кораблів у морі, описаний у прикладі,\(\PageIndex{5}\) приписується грецькому філософу Фалесу (бл. 600 р. До н.е.). Ми знаємо від різних авторів, що теорема ASA використовувалася для вимірювання відстаней з давніх часів, Існує історія, що один з офіцерів Наполеона використовував теорему ASA для вимірювання ширини річки, яку його армія повинна була перетнути, (див. Завдання 25 нижче.)
Проблеми
1 - 4. Для кожного з наступних (1) намалюйте трикутник з двома кутами і включеною стороною і (2) виміряйте решту сторін і кут,
1. \(\triangle ABC\)з\(\angle A = 40^{\circ}\),\(\angle B = 50^{\circ}\), і\(AB = 3\) дюймів,
2. \(\triangle DEF\)з\(\angle D = 40^{\circ}\),\(\angle E = 50^{\circ}\), і\(DE = 3\) дюймів,
3. \(\triangle ABC\)з\(\angle A = 50^{\circ}\),\(\angle B = 40^{\circ}\), і\(AB = 3\) дюймів,
4. \(\triangle DEF\)з\(\angle D = 50^{\circ}\),\(\angle E = 40^{\circ}\), і\(DE = 3\) дюймів.
5 - 8. Назвіть сторону, що входить між кутами:
5. \(\angle A\)і\(\angle B\) в\(\triangle ABC\).
6. \(\angle X\)і\(\angle Y\) в\(\triangle XYZ\).
7. \(\angle D\)і\(\angle F\) в\(\triangle DEF\).
8. \(\angle S\)і\(\angle T\) в\(\triangle RST\).
9 - 22. Для кожного з наступних
(1) написати заяву про конгруентність для двох трикутників,
(2) дати причину (1) (SAS, ASA або AAS теореми),
(3) знайти\(x\), або\(x\) і\(y\).
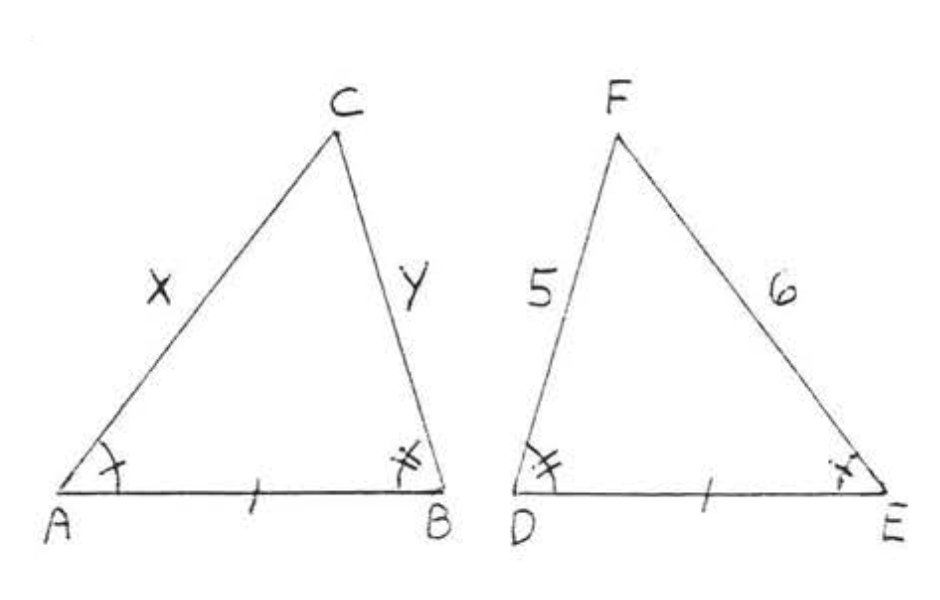
9.  10.
10. 
11. 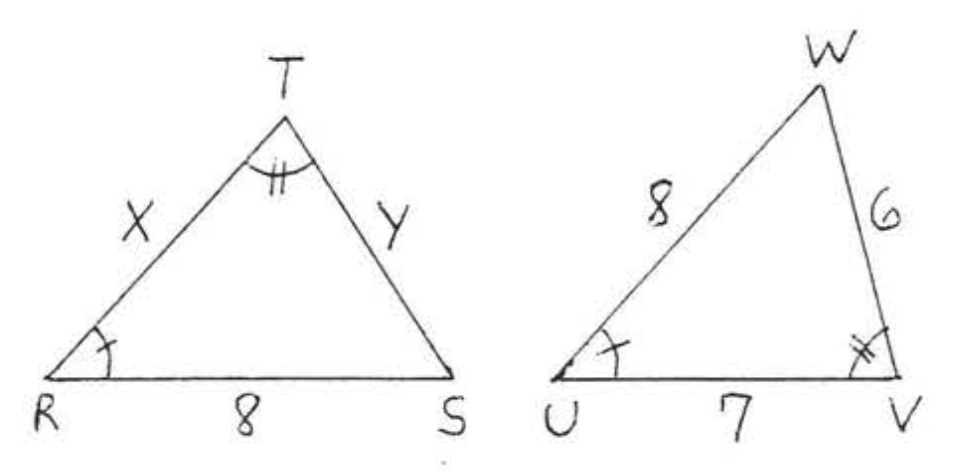 12.
12. 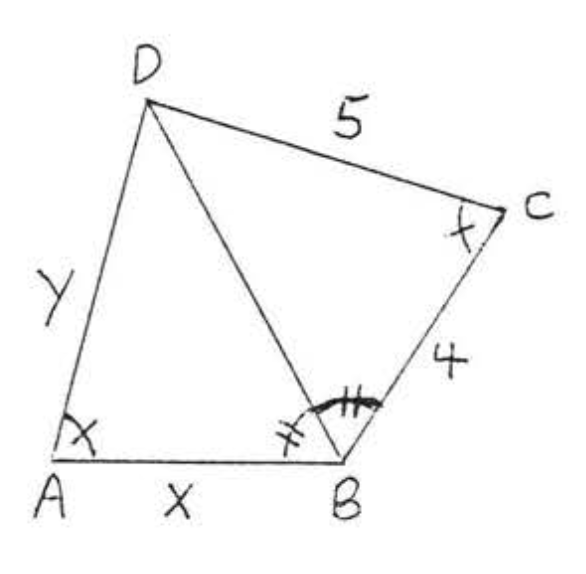
13.  14.
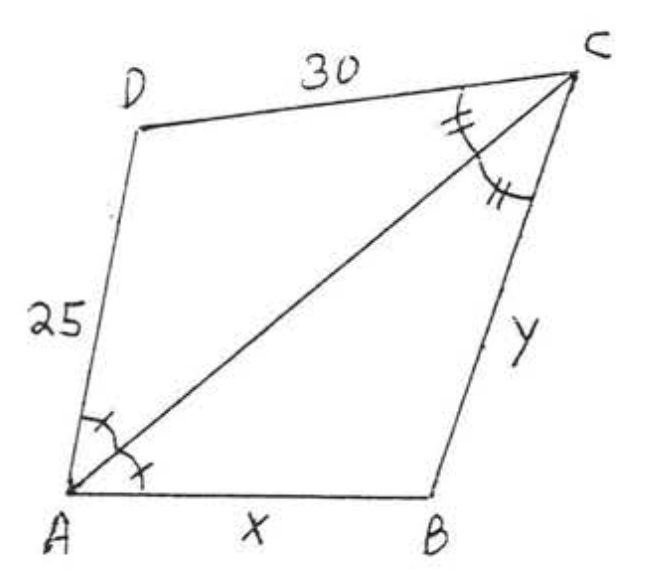
14. 
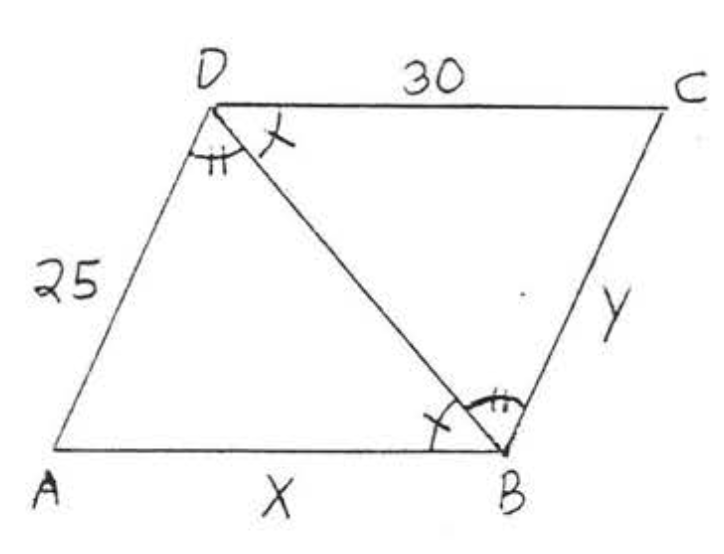
15. 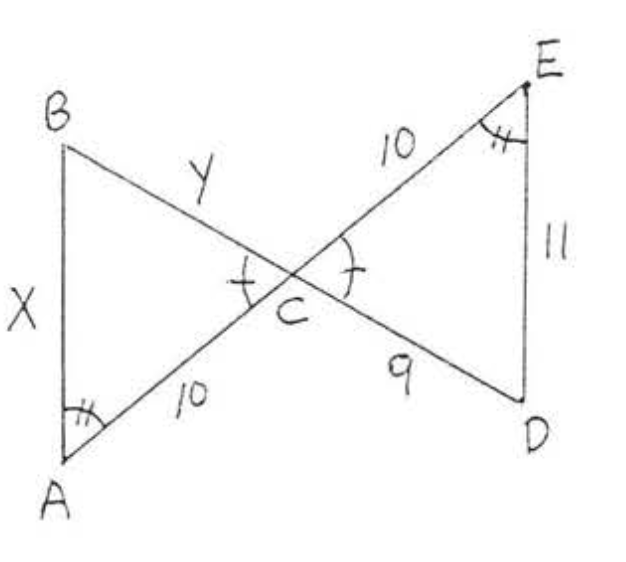 16.
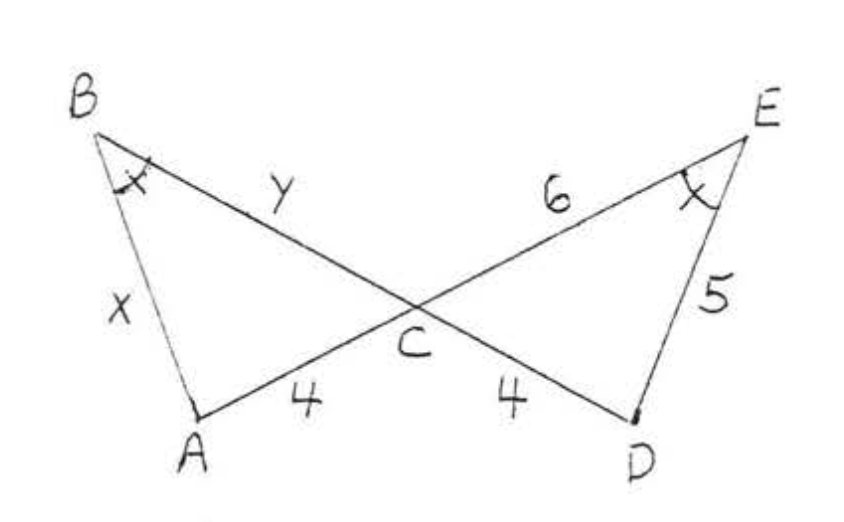
16. 
17. 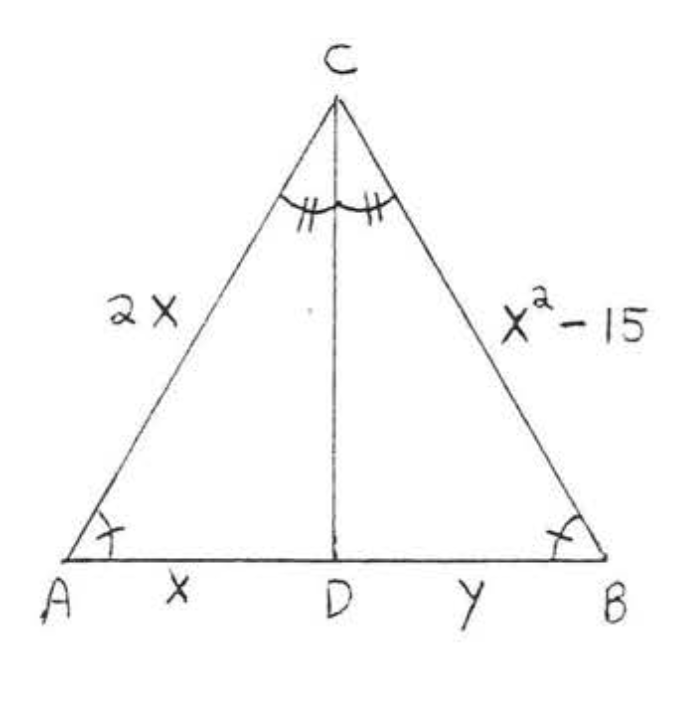 18.
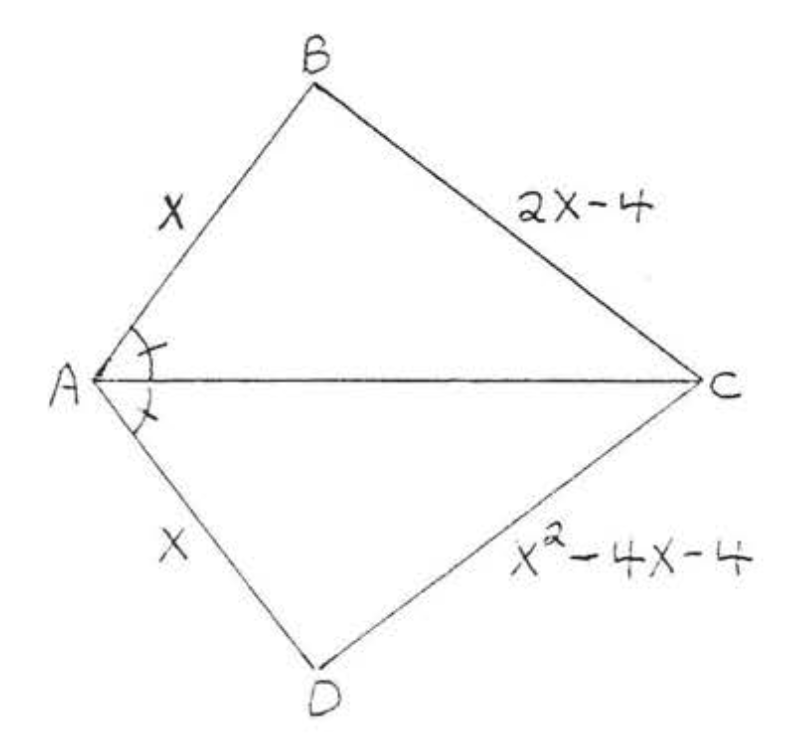
18. 
19. 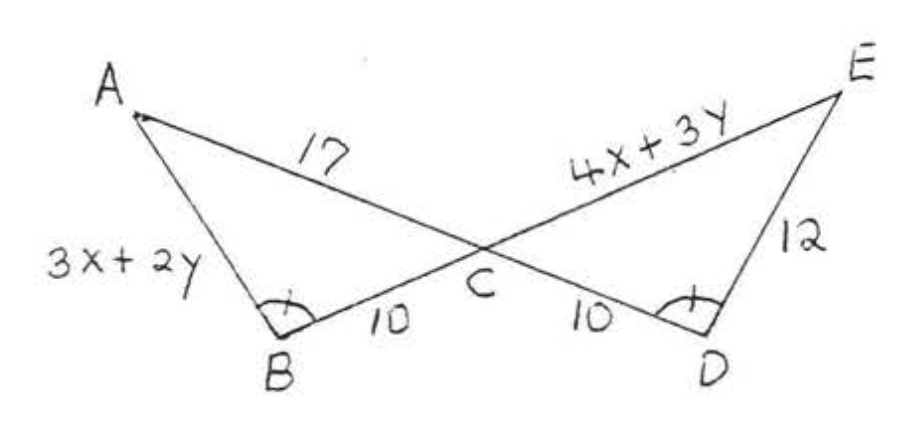 20.
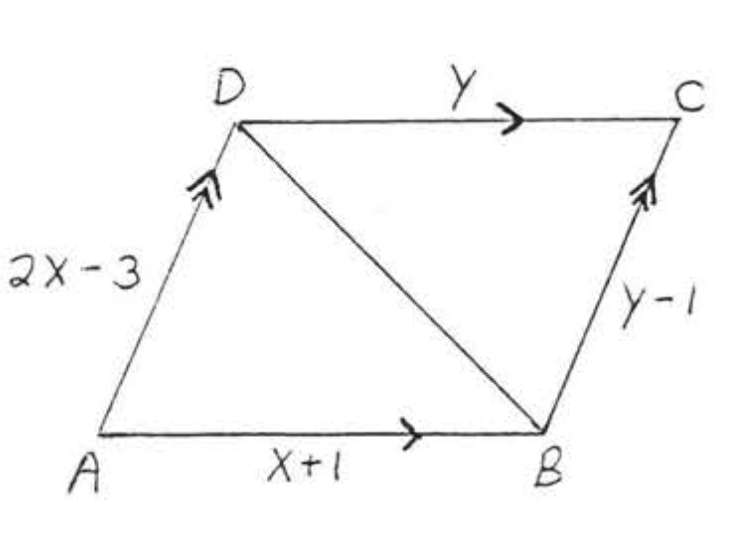
20. 
21. 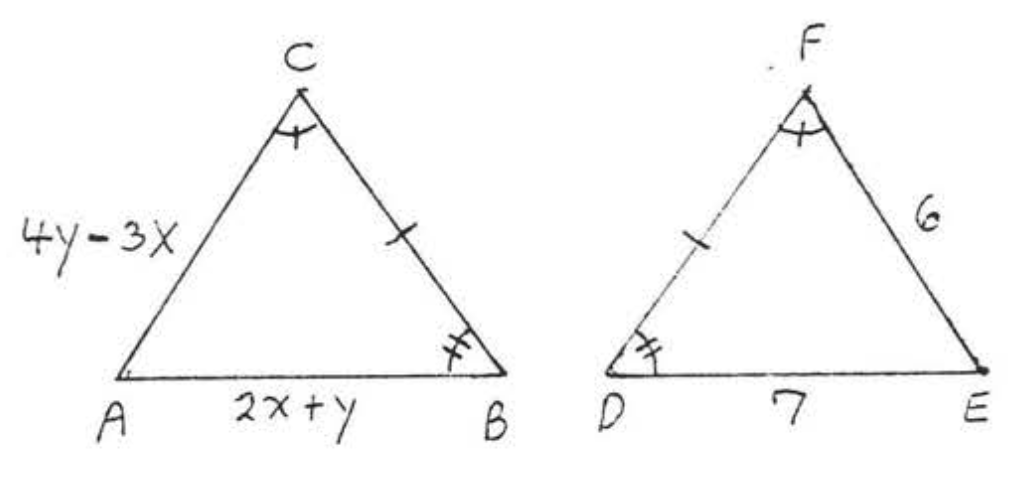 22.
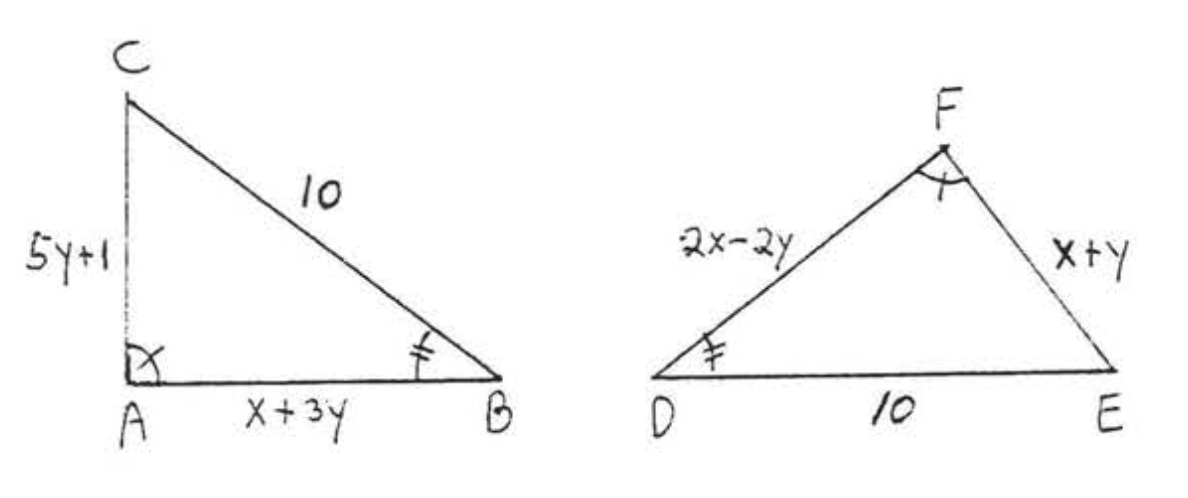
22. 
23 - 26. Для кожного з наведених нижче, включіть заяву про конгруентність та причину як частину вашої відповіді:
23. На схемі наскільки далеко знаходиться корабель S від точки\(P\) на узбережжі?
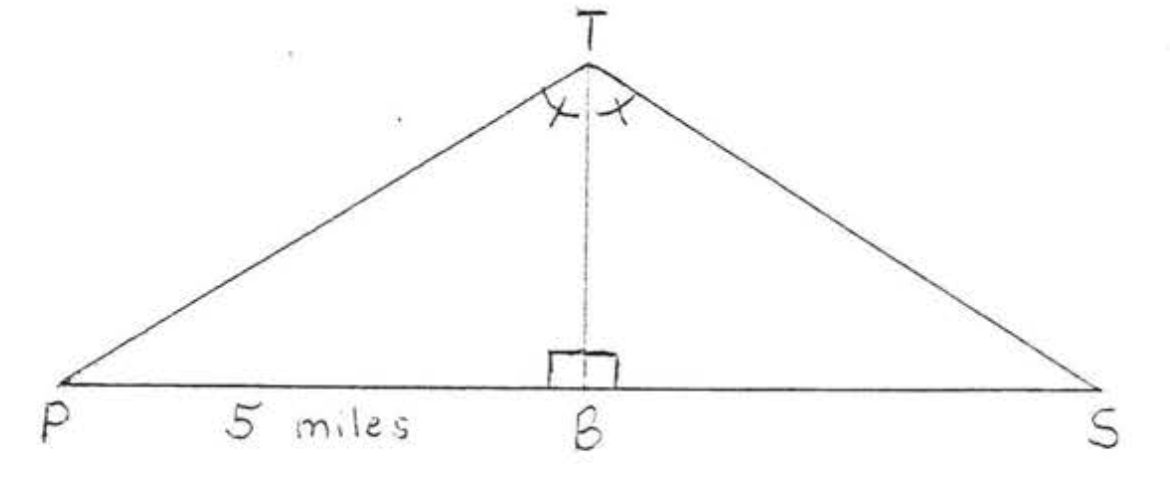
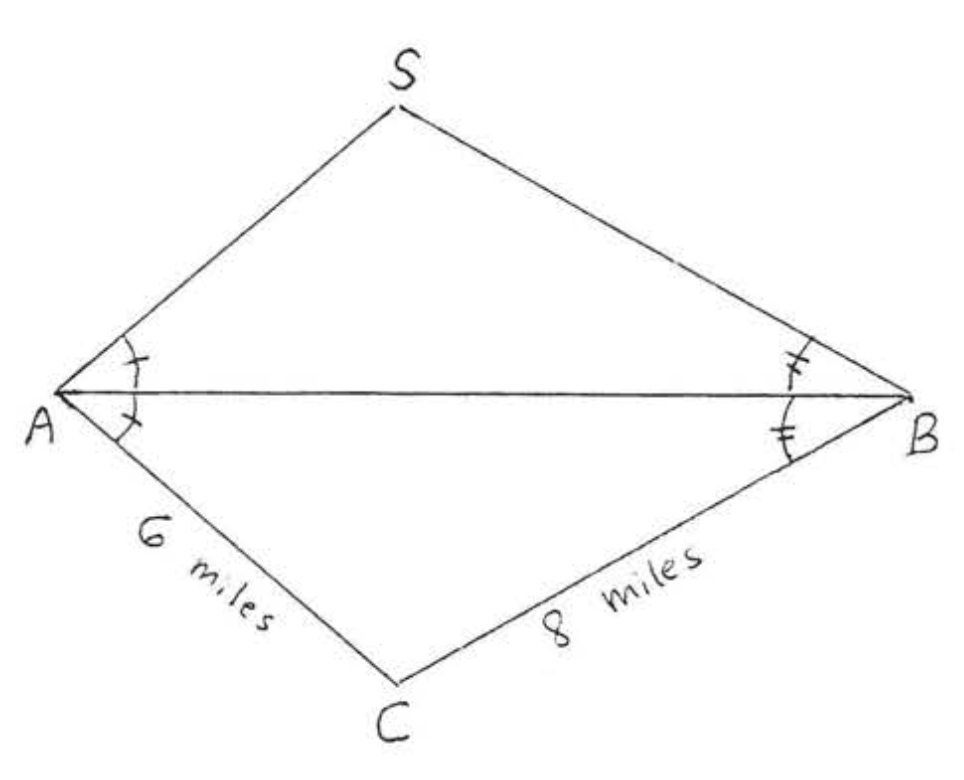
24. Корабель\(S\) спостерігається з точок\(A\) і\(B\) вздовж узбережжя. Трикутник\(ABC\) потім будується і вимірюється, як на схемі, Як далеко знаходиться корабель від точки\(A\)?
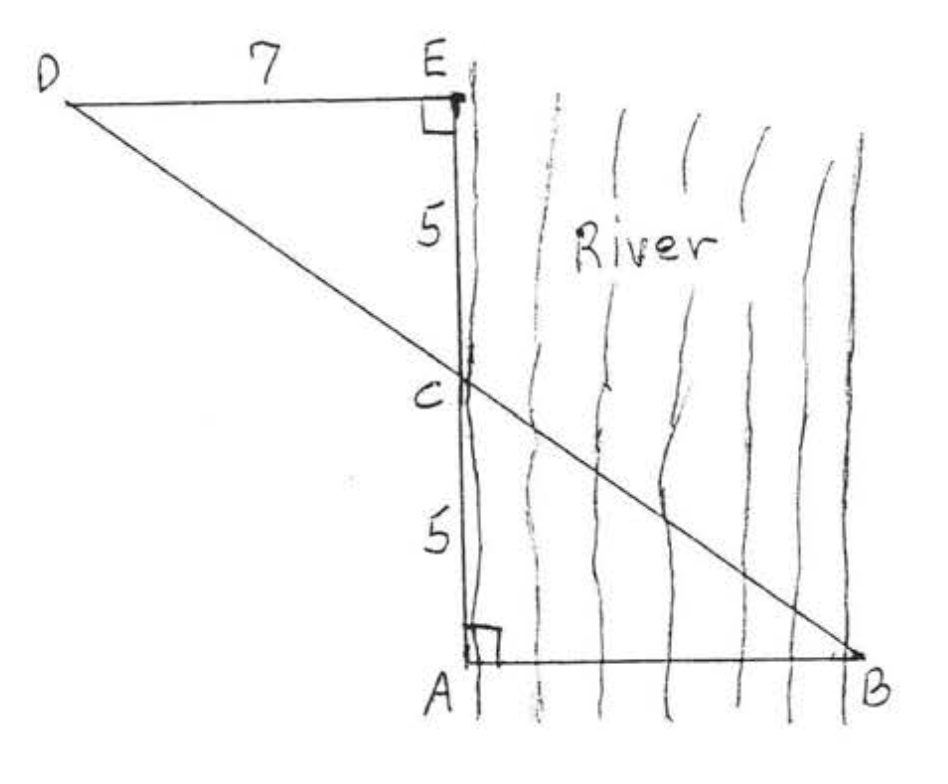
25. Знайдіть відстань\(AB\) через річку, якщо\(AC = CD = 5\) і\(DE = 7\) як на схемі.
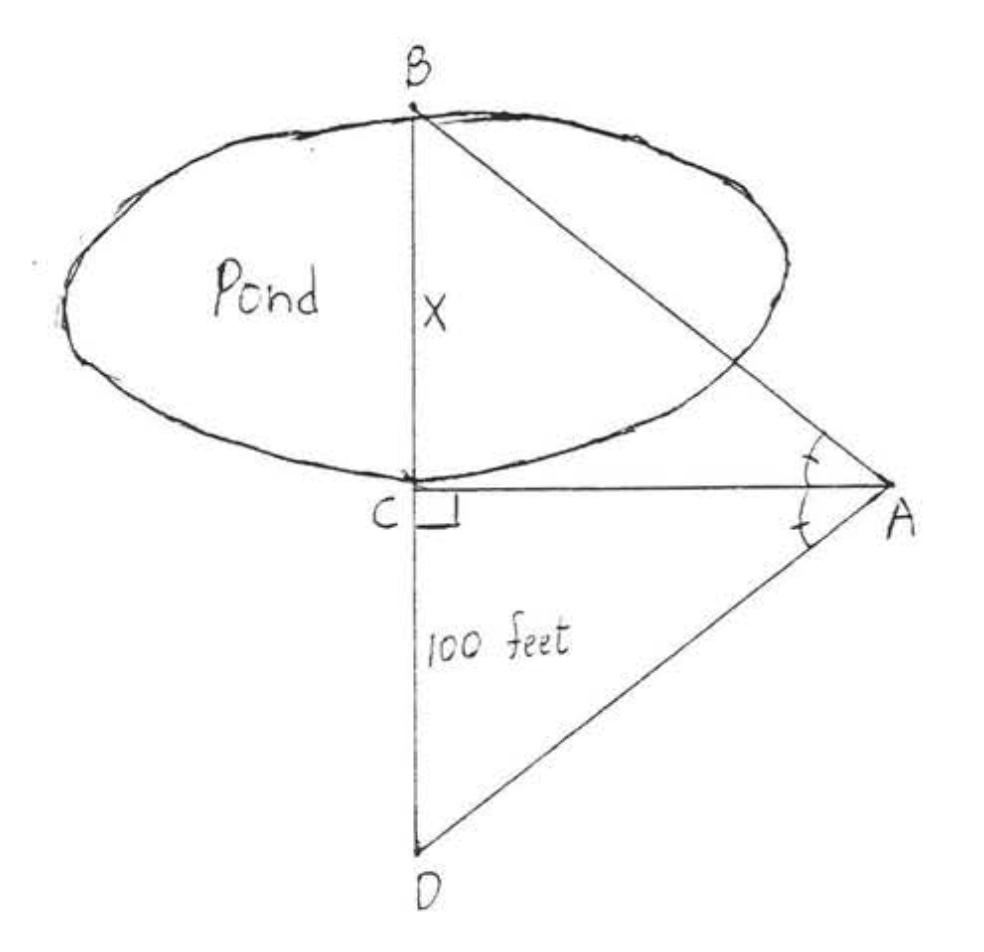
26. яка відстань через водойму?