Skip to main content
LibreTexts - Ukrayinska

4.4: Симетрія

  1. Last updated
  2. Save as PDF
  • Page ID
    58475

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    4.4.1 Досліджуйте симетрії

    Визначення: Симетрія

    Безліч точок А має симетрію типу T для деякого перетворення T тоді і тільки тоді, коли T (A) = A.

    Підтвердити T (x, y) = (-y, x) є симетрією множини {(1, 1), (-1, 1), (-1, -1), (1, -1)}.

    Продемонструвати T (x, y) = (-y, x) не є симетрією множини {(0, 0), (1, 0), (1, 1), (0, 1)}.

    Які точки потрібно додати до {(1, 1), (-1, 1), (-1, -1), (1, -1), (1, 0)} так що T (x, y) = (-y, x) є симетрією цієї множини?

    Перерахуйте всі симетрії квадрата, позначивши вершини та вказавши тип та параметри перетворень.

    Перерахуйте всі симетрії правильного n-стороннього багатокутника (n-кутника), позначивши вершини та вказавши тип та параметри перетворень.

    Для одного з правильних n-кутників перевірте наступне.

    1. Який склад двох обертальних симетрій?
    2. Яка композиція двох симетрій відображення?
    3. Яку найменшу кількість симетрій можна використовувати для генерації всіх симетрій?

    Намалюйте якийсь правильний n-кутник. Колір у n-кутник, щоб кольорова фігура підтримувала обертальну симетрію, але не відбивну симетрію.

    Намалюйте якийсь правильний n-кутник. Колір у n-кутник, щоб кольорова фігура зберігала відбивну симетрію, але не обертальну симетрію.

    Намалюйте фігуру, яка має поступальну симетрію.

    Намалюйте фігуру, яка має поступальну симетрію і рівно одну відбивну симетрію.

    Намалюйте фігуру, яка має поступальну симетрію і обертальну симетрію.

    Намалюйте фігуру, яка має дилатаційну симетрію.

    4.4.2 Дослідіть теселяції

    Визначення: Тесселяція

    Покриття площини - це теселяція тоді і тільки тоді, коли вона складається з однієї форми, нескінченно відтвореної за допомогою скінченної множини перетворень.

    Визначення: Плитка

    Покриття площини є плиткою тоді і тільки тоді, коли вона складається з скінченного набору форм, нескінченно відтворюваних за допомогою скінченної множини перетворень.

    Проаналізуйте теселяцію наступним чином.

    1. Визначте формуючу форму.
    2. Визначте найменший набір перетворень, які можуть генерувати теселяцію.
    3. Перерахуйте всі симетрії теселяції.
    4. Визначте найменший набір симетрій теселяції, який може генерувати всі симетрії теселяції.
    Визначення: Етикетка Конвея

    Наступне маркування теселяцій походить від книги «Симетрії речей» Джона Конвея, Хайді Бургіеля та Хаїма Гудмана-Штрауса. Виконайте наступні дії, щоб визначити та позначити тип групи симетрії теселяції. Отримане позначення називається підписом.

    1. Визначте всі лінії відображення.
    2. Якщо дві або більше ліній відображення перетинаються в точці, запишіть*n 1 n 2... де n 1, n 2 - кількість ліній, що перетинаються в кожній унікальній точці перетину.
    3. Якщо якась лінія відображення не перетинає інші лінії відображення, просто напишіть один * для кожної з них.
    4. Визначте будь-які обертання, які не є складом вже перерахованих відображень.
    5. Напишіть n 1 n 2... перед будь-яким * для кожного обертання, де n 1, n 2 - порядок обертань.
    6. Визначте будь-які роздуми ковзання, які не є складом відображень або обертань, які вже перераховані.
    7. Напишіть × в кінці підпису для кожного з цих роздумів ковзання.
    8. Визначте будь-які переклади, які не є складом інших симетрій, які вже перераховані.
    9. Напишіть ○ на передній частині підпису для кожної пари цих перекладів.

    Див. приклад підписів на рисунках\(\PageIndex{1}\) до\(\PageIndex{4}\).

    Знайдіть підписи двох теселяцій з архіву класів тут. Ви не можете вибрати два з однаковим підписом.

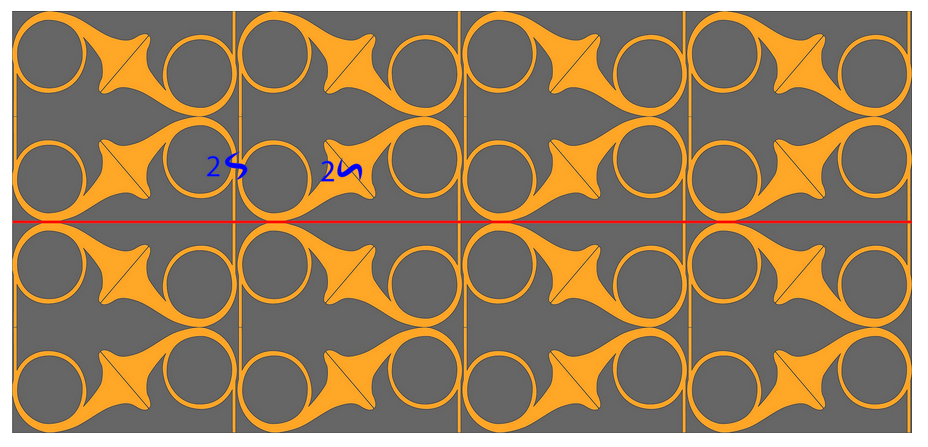
    Знайти підпис теселяції на рис\(\PageIndex{1}\).

    Почніть проект теселяції.

    4.4.3 Теселяційні зображення

    4.4.1.PNG
    Малюнок\(\PageIndex{1}\): Теселяція
    4.4.2.png
    Малюнок\(\PageIndex{2}\): Підпис *236 (Варіація на тему Скотта Розмана)
    4.4.3.png
    Малюнок\(\PageIndex{3}\): Підпис 22*
    4.4.4.PNG
    Малюнок\(\PageIndex{4}\): Підпис*X