Skip to main content
LibreTexts - Ukrayinska

3.3: Одночасний

  1. Last updated
  2. Save as PDF
  • Page ID
    58464

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Визначення: Медіана

    Лінія є медіаною тоді і тільки тоді, коли вона з'єднує вершину трикутника з серединою протилежної сторони.

    3.3.1 Досліджуйте

    Geogebra буде корисним для виконання цих експериментів. Будьте настільки докладні, як ви можете зі своїми домислами.

    Використовуйте приклад Geogebra,\(\PageIndex{1}\) щоб експериментувати з співвідношенням трьох перпендикулярних бісектрис трикутника. Перемістіть вершини трикутника навколо. Що залишається вірним щодо перпендикулярної бісектриси?

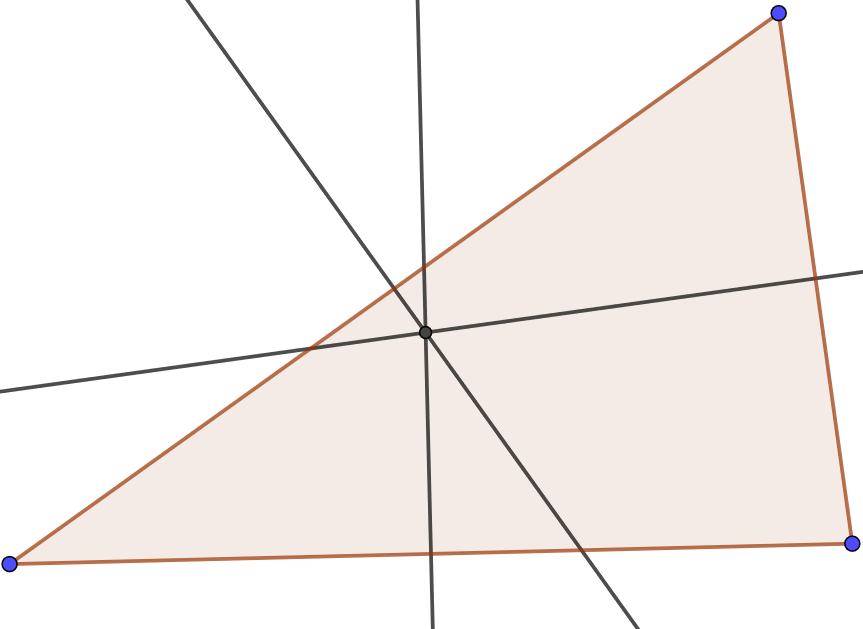
    3.3.1.jpg
    Малюнок\(\PageIndex{1}\): GeoGebra: Перпендикулярні бісектриси

    Використовуйте приклад Geogebra,\(\PageIndex{2}\) щоб експериментувати з відносинами трьох медіанів трикутника. Перемістіть вершини трикутника навколо. Що залишається правдою про медіани?

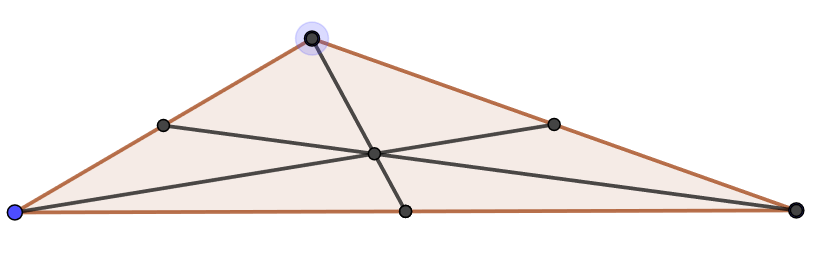
    3.3.2.png
    Малюнок\(\PageIndex{2}\): GeoGebra: Медіани

    Використовуйте приклад Geogebra,\(\PageIndex{3}\) щоб експериментувати з співвідношенням трьох кутових бісектрис трикутника. Перемістіть вершини трикутника навколо. Що залишається вірним щодо бісектриси кута?

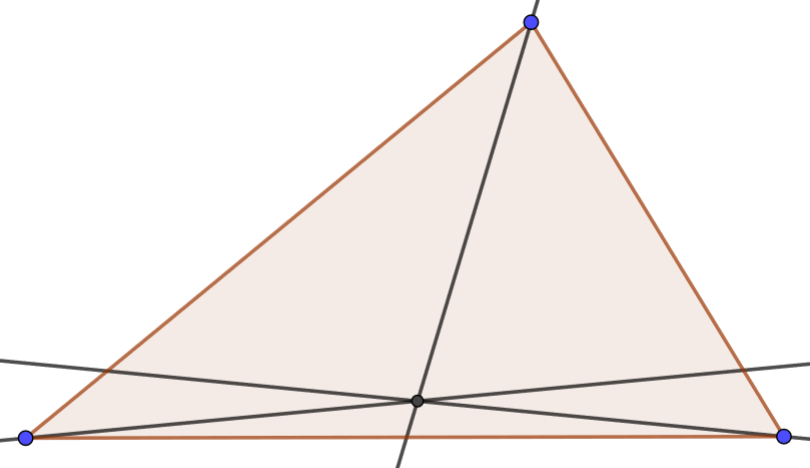
    3.3.3.jpg
    Малюнок\(\PageIndex{3}\): GeoGebra: Кутові бісектриси

    Використовуйте приклад Geogebra,\(\PageIndex{4}\) щоб експериментувати з співвідношенням трьох висот трикутника. Перемістіть вершини трикутника навколо. Що залишається вірним щодо висот?

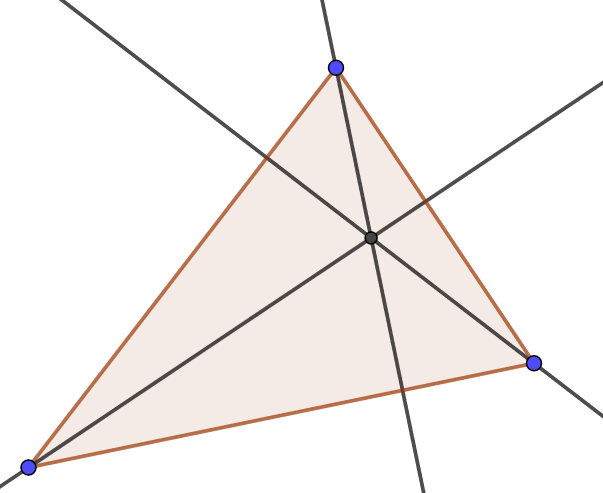
    3.3.4.png
    Малюнок\(\PageIndex{4}\): GeoGebra: Висоти

    Побудувати △ ABC. Побудувати △ XYZ такі, що X-B-Y, Y-C-Z, Z-A-X і XY ll AC, YZ ll AB, ZX ll BC. Побудувати перпендикулярні бісектриси △ XYZ. Що, здається, вірно з ними стосовно △ ABC.

    3.3.2 Довести

    Лемма

    Розглянемо три точки A, B, C з 1 і 2 перпендикулярними бісектрисами AB і BC відповідно. Нехай М 2 = 2 до н.е. Показати 1 ll ➤ 2 передбачає існування D = 2 AB таким чином, що A, B і D є колінеарними, а BDM 2 є прямим кутом.

    Теорема: Перпендикулярні бісектриси

    Доведіть гіпотезу про перпендикулярну бісектрису.

    Теорема: Циркумцентр

    Три точки однозначно визначають коло.

    Лемма

    Два медіани перетинаються в точці 2/3 шляху вниз обидва медіани.

    Теорема: Медіанс

    Доведіть здогадки про медіани.

    Теорема

    Точка знаходиться на бісектрисі кута тоді і лише тоді, коли він рівновіддалений від обох сторін кута.

    Теорема: Кутові бісектриси

    Доведіть гіпотезу про кутові бісектриси.

    Теорема: Інцентр

    Для кожного трикутника існує коло всередині і дотична до всіх трьох сторін.

    Теорема: Висоти

    Доведіть здогадки про висотах.