19.1: Класичні проблеми

Last updated
Save as PDF

Page ID: 59149

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми перерахуємо пару класичних будівельних проблем; кожна відома вже більше тисячі років.

Рішення двох наступних проблем досить нетривіальні.

Проблема$\PageIndex{1}$ Problem of Brahmagupta

Побудувати вписаний чотирикутник з заданими сторонами.

Проблема$\PageIndex{1}$ Problem of Apollonius

Побудувати коло, яке є дотичним до трьох заданих кіл.

$2021-03-02 пнг$

Кілька рішень цієї проблеми, заснованих на різних ідеях, представлені в [9]. Наступна вправа є спрощеною версією проблеми Аполлонія, яка до сих пір нетривіальна.

Вправа$\PageIndex{1}$

Побудувати коло, яке проходить через задану точку і є дотичною до двох пересічних ліній.

Підказка

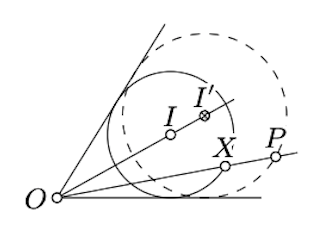
$2021-03-02 пнг$

$O$Дозволяти точка перетину ліній. Побудуйте коло$\Gamma$, дотичну до обох ліній, хрестиків$[OP)$; позначимо його центр по$I$. Припустимо, що$X$ позначає одну з точок перетину$\Gamma$ і$[OP)$.

Побудуйте$I' \in [OI)$ таку точку, що$\dfrac{OI'}{OI} = \dfrac{OP}{OX}$. Зверніть увагу, що коло, що проходить через$P$ і по центру$I'$, є рішенням.

Наступні три проблеми не можуть бути вирішені в принципі, тобто потрібної конструкції компаса і лінійки не існує.

Подвоєння куба

Побудуйте сторону нового куба, обсяг якого вдвічі більший за об'єм даного куба.

Іншими словами, з огляду на відрізок довжини$a$, потрібно побудувати відрізок довжини$\sqrt[3]{2}\cdot a$.

Квадратування кола

Побудуйте квадрат з тією ж площею, що і задане коло.

Якщо радіус$r$ заданої окружності, нам потрібно побудувати відрізок довжини$\sqrt{\pi}\cdot r$.

Насправді не існує конструкції компаса та лінійки, яка перетинає кут з мірою$\dfrac{\pi}{3}$. Наявність такої конструкції означало б конструктивність правильного 9-кутника, що заборонено наступним відомим результатом:

Правильний$n$ -кутник, вписаний в коло з центром,$O$ - це послідовність точок$A_1\dots A_n$ на колі така, що

$\measuredangle A_nOA_1=\measuredangle A_1OA_2=\dots=\measuredangle A_{n-1}OA_n=\pm\tfrac2n\cdot \pi.$

$A_1,\dots, A_n$Точки - це вершини,$[A_1A_2], \dots, [A_nA_1]$ відрізки - сторони, а решта$[A_iA_j]$ відрізків - діагоналі$n$ -кутника.

А конструкція правильного$n$ -кутника, отже, зводиться до побудови кута з розмірами$\tfrac2n\cdot \pi$.

Теорема$\PageIndex{1}$ Gauss-Wantzel theorem

Правильний$n$ -кутник може бути побудований за допомогою лінійки та циркуля тоді і лише тоді, коли$n$ є добутком потужності$2$ та будь-якої кількості різних простих чисел Ферма.

Просте число Ферма - це просте число у вигляді$2^k+1$ деякого цілого числа$k$. Сьогодні відомі лише п'ять простих чисел Fermat:

3, 5, 17, 257, 65537.

Наприклад,

можна побудувати правильний 340-кутник, так$5$ як$340=2^2\cdot 5\cdot 17$ і$17$ є простими числами Ферма;
не можна побудувати правильний 7-кутник, оскільки не$7$ є простим Fermat;
неможливо побудувати правильний 9-кутник; altho$9=3\cdot 3$ є добутком двох простих чисел Ферма, ці прості числа не відрізняються.

Неможливість цих споруд була доведена лише в 19 столітті. Спосіб, який використовується в доказах, вказується в наступному розділі.

Проблема\(\PageIndex{1}\) Problem of Brahmagupta

Проблема\(\PageIndex{1}\) Problem of Apollonius

Вправа\(\PageIndex{1}\)

Подвоєння куба

Квадратування кола

Теорема\(\PageIndex{1}\) Gauss-Wantzel theorem