19.2: Побудовані номери

Last updated
Save as PDF

Page ID: 59148

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У класичних конструкціях компаса і лінійки початкова конфігурація може бути повністю описана кінцевою кількістю точок; кожна лінія визначається двома точками на ній, а кожне коло описується своїм центром і точкою на ньому (рівнозначно можна описати коло трьома точками на ньому).

Таким же чином результат будівництва можна описати кінцевим набором балів.

Ми завжди можемо припустити, що початкова конфігурація має принаймні дві точки; якщо не додати одну або дві точки до конфігурації. Більш того, застосовуючи масштабування на всю площину, можна вважати, що перші дві точки в початковій конфігурації лежать на відстані 1 один від одного.

У цьому випадку ми можемо вибрати систему координат, таку, що одна з початкових точок є початковою точкою,$(0,0)$ а ще одна початкова точка має координати$(1,0)$. У цій системі координат початкова конфігурація$n$ точок описується$2\cdot n-4$ числами — їх координатами$x_3,y_3,\dots,x_n,y_n$.

Виявляється, координати будь-якої точки, побудованої за допомогою циркуля і лінійки, можуть бути записані через числа,$x_3,y_3,\dots,x_n,y_n$ використовуючи чотири арифметичні операції «$+$","$-$", "$\cdot$", «$/$"і квадратний корінь» $\sqrt{\phantom{a}}$".

Наприклад, припустимо, що ми хочемо знайти$X_2=(x_2,y_2)$ точки$X_1=(x_1,y_1)$ і перетинів лінії, що проходить через$A=(x_A,y_A)$$B=(x_B,y_B)$ і коло з центром$O=(x_O,y_O)$, який проходить через точку$W=(x_W,y_W)$. Запишемо рівняння кола і прямої в координатах$(x,y)$:

Зверніть увагу, що$(x_2,y_2)$ координати$(x_1,y_1)$ і точки$X_1$ і$X_2$ є рішеннями цієї системи. Висловлюючи$y$ з другого рівняння і підставляючи результат в перше, дає нам квадратне рівняння в$x$, яке можна вирішити за допомогою "$+$"$-$","$\cdot$", "$/$"і» $\sqrt{\phantom{a}}$"тільки.

Те ж саме можна виконати і для перетину двох кіл. Перетин двох рядків ще простіше; він описується як рішення двох лінійних рівнянь і може бути виражений лише чотирма арифметичними операціями; квадратний корінь "$\sqrt{\phantom{a}}$"не потрібен.

З іншого боку, легко виготовити конструкції компас-лінійки, які виробляють відрізки довжин$a+b$ і$a-b$ з двох заданих відрізків довжин$a>b$.

Для виконання "$\cdot$","$/$" і "$\sqrt{\phantom{a}}$"розглянемо наступну схему: нехай$[AB]$ буде діаметр кола; зафіксувати точку$C$ на колі і нехай$D$ буде точка стопи$C$ на $[AB]$. За наслідком 9.3.1 кут$ACB$ правильний. Тому

$\triangle ABC\sim\triangle ACD\sim \triangle CBD.$

Звідси випливає, що$AD\cdot BD=CD^2$.

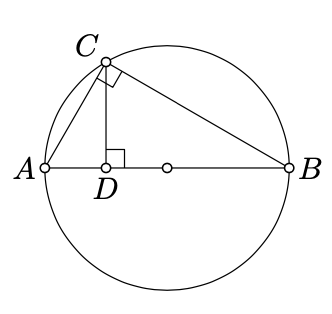
$2021-03-02 пнг$

Використовуючи цю схему, слід вгадати рішення наступної вправи.

Вправа$\PageIndex{1}$

Дано два відрізки лінії з відрізками$a$ і$b$, дають лінійку і компас побудова відрізків з довжиною$\tfrac {a^2}b$ і$\sqrt{a\cdot b}$.

Підказка

Побудувати$\sqrt{a \cdot b}$: (1) побудувати точки$A, B$, і$D \in [AB]$ такі, що$AD = a$ і$BD =b$; (2) побудувати коло$\Gamma$ на діаметрі$[AB]$; (3) провести лінію$\ell$ через$D$ перпендикулярно$(AB)$; (4) нехай$C$ буде перетин$\Gamma$ і$\ell$. Потім$DC = \sqrt{a \cdot b}$.

$\dfrac{a^2}{b}$Конструкція аналогічна.

$a$Беручи$1$ за або$b$ вище, ми можемо виробляти$\sqrt a$,$a^2$,$\tfrac1b$. Поєднуючи ці конструкції ми можемо виробляти$a\cdot b=(\sqrt{a\cdot b})^2$,$\tfrac ab=a\cdot\tfrac 1b$. Іншими словами, ми створили калькулятор компаса і лінійки$+$", який може робити "$-$","$\cdot$", "$/$", і"$\sqrt{\phantom{a}}$".

Дискусія вище дає ескіз доказу наступної теореми:

Теорема$\PageIndex{1}$

Припустимо, що початкова конфігурація геометричної конструкції задається точками$A_1=(0,0)$,$A_2=(1,0)$,$A_3=(x_3,y_3),\dots,A_n=(x_n,y_n)$. Тоді точка$X=(x,y)$ може бути побудована за допомогою конструкції компаса і лінійки тоді і тільки тоді, коли обидві координати$x$ і$y$ можуть бути виражені з цілих чисел і$x_3$$y_3$,$x_4$, $y_4,\dots,x_n,y_n$за допомогою арифметичних операцій "$+$"$-$","$\cdot$", "$/$", і квадратного кореня"$\sqrt{\phantom{a}}$".

Числа, які можуть бути виражені з заданих чисел за допомогою арифметичних операцій і квадратного кореня «$\sqrt{\phantom{a}}$» називаються конструктивними; якщо список заданих чисел не задано, то ми можемо використовувати тільки цілі числа.

Теорема вище перекладає будь-яку задачу побудови компаса і лінійки на чисто алгебраїчну мову. Наприклад:

Неможливість розв'язку подвоєння задачі куба стверджує, що не$\sqrt[3]{2}$ є конструктивним числом. Це$\sqrt[3]{2}$ не може бути виражено через цілі числа$+$", використовуючи "$-$","$\cdot$", "$/$", і"$\sqrt{\phantom{a}}$".
Неможливість рішення для квадратизації кола говорить про те$\sqrt{\pi}$, що, або еквівалентно$\pi$, не є конструктивним числом.
Теорема Гаусса—Вантцеля говорить, для яких цілих чисел$n$ число$\cos\tfrac{2\cdot\pi}n$ можна побудувати.

Деякі з цих тверджень можуть виглядати очевидними, але суворі докази вимагають певних знань з абстрактної алгебри (а саме теорії поля), яка виходить за рамки цієї книги.

У наступному розділі ми обговоримо аналогічні, але більш прості приклади неможливих конструкцій з незвичайним інструментом.

Вправа$\PageIndex{2}$

Покажіть, що діагональ або правильний п'ятикутник в$\tfrac{1+\sqrt5}2$ рази більше його боку.
Використовуйте (а), щоб зробити конструкцію компаса і лінійки регулярного п'ятикутника.

Підказка

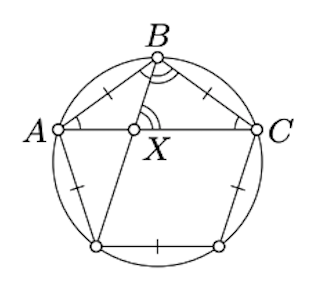
$2021-03-02 пнг$

(а) Подивіться на діаграму правильного п'ятикутника; покажіть, що кути, позначені таким же чином, мають однакову кутову міру. Зробіть висновок про те, що$XC =BC$ і$\triangle ABC \sim \triangle AXB$. Тому

$\dfrac{AB}{AC} = \dfrac{AX}{AB} = \dfrac{AC - AB}{AB} = \dfrac{AC}{AB} - 1$.

Залишилося вирішити за$\dfrac{AC}{AB}$.

(b) Виберіть дві точки$P$$Q$ і скористайтеся калькулятором компаса та лінійки для побудови двох точок$V$ і$W$ таких, що$VW = \dfrac{1 + \sqrt{5}}{2} \cdot PQ$. Потім спорудити п'ятикутник зі сторонами$PQ$ і діагоналями$VW$.

Вправа\(\PageIndex{1}\)

Теорема\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)