18.4: Формула Ейлера

Last updated
Save as PDF

Page ID: 59177

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

$\alpha$Дозволяти бути дійсним числом. Наступна ідентичність називається формулою Ейлера:

\[e^{i\cdot\alpha}=\cos\alpha+i\cdot\sin\alpha.\]

Зокрема,$e^{i\cdot\pi}=-1$ і$e^{i\cdot\frac\pi2}=i$.

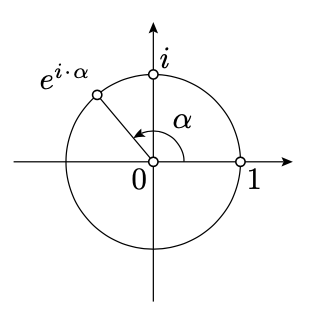
$2021-03-01 пнг$

Геометрично формула Ейлера означає наступне: Припустимо, що$O$ і$E$ є точками зі складними координатами$0$ і$1$ відповідно. Припустимо

$OZ=1\quad \text{and}\quad \measuredangle EOZ \equiv \alpha,$

$e^{i\cdot\alpha}$то комплексна координата$Z$. Зокрема, комплексна координата будь-якої точки на одиничному колі з центром$O$ може бути однозначно виражена як$e^{i\cdot\alpha}$ для деяких$\alpha\in(-\pi,\pi]$.

Чому ви повинні думати, що 18.4.1 це правда?

Доказ ідентичності Ейлера залежить від способу визначення експоненціальної функції. Якщо вам ніколи не доводилося застосовувати експоненціальну функцію до уявного числа, ви можете взяти праву частину в 18.4.1 як визначення$e^{i\cdot\alpha}$.

В цьому випадку формально нічого не доводиться доводити, але краще перевірити, що$e^{i\cdot\alpha}$ задовольняє знайомі ідентичності. Головним чином,

$e^{i\cdot \alpha}\cdot e^{i\cdot \beta}= e^{i\cdot(\alpha+\beta)}.$

Останнє можна довести за допомогою 18.1.2 і наступних тригонометричних формул, які ми вважаємо відомими:

$\begin{aligned} \cos(\alpha+\beta)&=\cos\alpha\cdot\cos\beta-\sin\alpha\cdot\sin\beta, \\ \sin(\alpha+\beta)&=\sin\alpha\cdot\cos\beta+\cos\alpha\cdot\sin\beta.\end{aligned}$

Якщо ви знаєте ряди степенів для синуса, косинуса та експоненціальної функції, то наступне може переконати, що ідентичність 18.4.1 має:

$\begin{aligned} e^{i\cdot \alpha } &{}= 1 + i\cdot \alpha + \frac{(i\cdot \alpha )^2}{2!} + \frac{(i\cdot \alpha )^3}{3!} + \frac{(i\cdot \alpha )^4}{4!} + \frac{(i\cdot \alpha )^5}{5!} + \cdots = \\ &= 1 + i\cdot \alpha - \frac{\alpha ^2}{2!} - i\cdot\frac{ \alpha ^3}{3!} + \frac{\alpha ^4}{4!} + i\cdot\frac{ \alpha ^5}{5!} - \cdots = \\ &= \left( 1 - \frac{\alpha ^2}{2!} + \frac{\alpha ^4}{4!} - \cdots \right) + i\cdot\left( \alpha - \frac{\alpha ^3}{3!} + \frac{\alpha ^5}{5!} - \cdots \right) = \\ &= \cos \alpha + i\cdot\sin \alpha.\end{aligned}$