13.6: теорема Піфагора

Last updated
Save as PDF

Page ID: 58961

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Нагадаємо, що$\cosh$ позначає гіперболічний косинус; тобто функцію, визначену

$\cosh x := \dfrac{e^x+e^{-x}}2.$

Теорема$\PageIndex{1}$ Hyperbolic Pythagorean theorem

Припустимо, що$ACB$ це h-трикутник з прямим кутом в$C$. Набір

$a = BC_h,$$b = CA_h$і$c = AB_h$.

Тоді

\[\cosh c = \cosh a \cdot \cosh b.\]

Формула 13.6.1 буде доведена за допомогою прямих розрахунків. Перш ніж давати докази, обговоримо граничні випадки цієї формули.

Зверніть увагу, що$\cosh x$ може бути написано за допомогою розширення Тейлора

$\cosh x=1+\dfrac{1}{2}\cdot x^2+\dfrac{1}{24}\cdot x^4+\dots.$

Звідси випливає$a$$b$, що якщо, і$c$ маленькі, то

$\begin{array} {rcl} {1 + \dfrac{1}{2} \cdot c^2} & \approx & {\cosh c = \cosh a \cdot \cosh b \approx} \\ {} & \approx & {(1 + \dfrac{1}{2} \cdot a^2)(1 + \dfrac{1}{2} \cdot b^2) \approx} \\ {} & \approx & {1 + \dfrac{1}{2} \cdot (a^2 + b^2).} \end{array}$

Іншими словами, вихідна теорема Піфагора (Теорема 6.2.1) є граничним випадком гіперболічної теореми Піфагора для малих трикутників.

Для великих$a$ і$b$ термінів$e^{-a}$$e^{-b}$, і$e^{-a-b+\ln 2}$ нехтуються. У цьому випадку ми маємо такі наближення:

$\begin{array} {\cosh a \cdot \cos h b} & \approx & {\dfrac{e^a}{2} \cdot \dfrac{e^b}{2} =} \\ {} & = & {\dfrac{e^{a+b-\ln 2}}{2} \approx} \\ {} & \approx & {\cosh (a+b-\ln 2)} \end{array}$

Тому$c \approx a+b-\ln 2$.

Вправа$\PageIndex{1}$

Припустимо, що$ACB$ це h-трикутник з прямим кутом в$C$. Набір$a=BC_h$,$b=CA_h$, і$c=AB_h$. Покажіть, що

$c+\ln 2>a+b.$

Підказка

Застосовують гіперболічну теорему Піфагора і визначення гіперболічного косинуса. Повинні допомогти наступні спостереження:

$x \mapsto e^x$є зростаючою позитивною функцією.
За нерівністю трикутника ми маємо$-c \le a - b$ і$-c \le b - a$

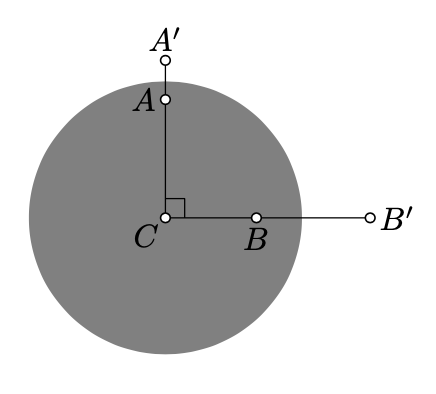
$2021-02-25 9.07.56.png$

У доведенні гіперболічної теореми Піфагора використовуємо наступну формулу з вправи 12.9.2:

$B$тут$A$, h-точки відмінні від центру абсолюту і$A'$,$B'$ є їх інверсії в абсолюті. Ця формула виведена в підказках.

Доказ теореми$\PageIndex{1}$. Припустимо, що абсолют - це одиничне коло. За основним спостереженням (теорема 12.3.1) можна припустити, що$C$ це центр абсолюту. Нехай$A'$ і$B'$ позначають зворотні$A$ і$B$ в абсолюті.

Набір$x=BC$,$y=AC$. За теоремою Лемма 12.3.2

$a = \ln \dfrac{1 + x}{1 - x}$,$b = \ln \dfrac{1 + y}{1 - y}.$

Тому

\[\begin{array} {rclcrcl} {\cosh a} & = & {\dfrac{1}{2} \cdot (\dfrac{1 + x}{1 - x} + \dfrac{1 - x}{1 + x}) =} & \ \ \ \ & {\cosh b} & = & {\dfrac{1}{2} \cdot (\dfrac{1 + y}{1 - y} + \dfrac{1 - y}{1 + y}) =} \\ {} & = & {\dfrac{1 + x^2}{1-x^2},} & \ \ \ \ & {} & = & {\dfrac{1 + y^2}{1 - y^2}.} \end{array}\]

Зверніть увагу, що

$B'C = \dfrac{1}{x},$$A'C = \dfrac{1}{y}.$

Тому

$BB' = \dfrac{1}{x} - x$,$AA' = \dfrac{1}{y} - y.$

Оскільки трикутники$ABC$,,$A'BC$$AB'C$,$A'B'C$ мають рацію, оригінальна теорема Піфагора (Теорема 6.2.1) має на увазі

$\begin{array} {rcl} {AB} & = & {\sqrt{x^2 + y^2}} \\ {A'B} & = & {\sqrt{x^2 + \dfrac{1}{y^2}},} \end{array}$$\begin{array} {rcl} {AB'} & = & {\sqrt{\dfrac{1}{x^2} + y^2,}} \\ {A'B'} & = & {\sqrt{\dfrac{1}{x^2} + \dfrac{1}{y^2}}.} \end{array}$

Відповідно до вправи 12.9.2,

\[\begin{array} {rcl} {\cosh c} & = & {\dfrac{AB \cdot A'B' + AB' \cdot A'B}{AA' \cdot BB'} = } \\ {} & = & {\dfrac{\sqrt{x^2 + y^2} \cdot \sqrt{\dfrac{1}{x^2} + \dfrac{1}{y^2}} + \sqrt{\dfrac{1}{x^2} + y^2} \cdot \sqrt{x^2 + \dfrac{1}{y^2}}}{(\dfrac{1}{y} - y) \cdot (\dfrac{1}{x} - x)} =} \\ {} & = & {\dfrac{x^2 + y^2 + 1 + x^2 \cdot y^2}{(1 - y^2) \cdot (1 - x^2)} =} \\ {} & = & {\dfrac{1 + x^2}{1 - x^2} \cdot \dfrac{1 + y^2}{1 - y^2}.} \end{array}\]

Нарешті, зауважте, що 13.6.2 та 13.6.3 означають 13.6.1.