13.1: Кут паралелізму

Last updated
Save as PDF

Page ID: 58979

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

$P$Дозволяти точка від h-лінії$\ell$. Падіння перпендикуляр$(PQ)_h$ від$P$ до$\ell$; нехай$Q$ бути його точка ноги. $\phi$Дозволяти найменшим значенням таким чином, що h-лінія$(PZ)_h$ з$|\measuredangle_h Q P Z|=\phi$ не перетинається$\ell$.

Значення$\phi$ називається кутом паралельності$P$ до$\ell$. Зрозуміло, що$\phi$ залежить тільки від h-відстані$s=PQ_h$. Далі,$\phi(s) \to \pi/2$ як$s \to 0$, і$\phi(s) \to 0$ як$s \to \infty$. (В евклідовій геометрії кут паралелізму однаково дорівнює$\pi/2$.)

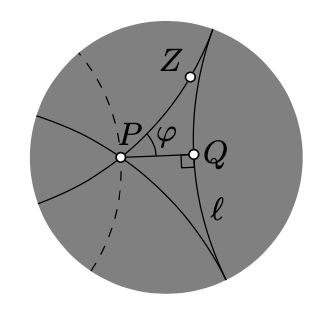
$2021-02-24 пнг$

Якщо$\ell$$P$, і$Z$ є як вище, то h-лінія$m=(PZ)_h$ називається асимптотично паралельно$\ell$. Іншими словами, дві h-лінії асимптотично паралельні, якщо вони поділяють одну ідеальну точку. (У гіперболічній геометрії термін паралельні лінії часто використовується для асимптотично паралельних ліній; ми не дотримуємося цієї умовності.)

Враховуючи$P \not\in \ell$, є рівно дві асимптотично паралельні лінії через$P$ до$\ell$; інші паралельні лінії називаються ультра паралельними.

На діаграмі дві суцільні h-лінії, що проходять через$P$ асимптотично паралельні$\ell$; пунктирна h-лінія ультра паралельна$\ell$.

Вправа$\PageIndex{1}$

Показати, що дві різні h-лінії$\ell$ і$m$ є ультрапаралельними тоді і тільки тоді, коли вони мають загальний перпендикуляр; тобто існує$h$ -лінія$n$ така, що$n \perp \ell$ і$n \perp m$.

Підказка

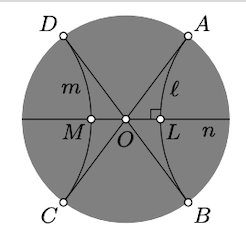
$2021-02-24 пнг$

Частина «тільки якщо». Припустимо$\ell$ і$m$ є ультрапаралельними; тобто вони не перетинаються і мають чіткі ідеальні точки. Позначимо ідеальні точки по$A, B, C$, і$D$; можна вважати, що вони з'являються на абсолюті в тому ж порядку. У цьому випадку h-лінія з ідеальними точками$A$ і$C$ перетинає h-лінію з ідеальними точками$B$ і$D$. Позначають по$O$ їх точці перетину.

За Lemma 12.3.1, можна припустити, що$O$ це центр абсолюту. Зверніть увагу, що$\ell$ це відображення$m$ поперек$O$ в евклідовому сенсі. Відкиньте h-перпендикуляр$n$ від$O$ до$\ell$, і покажіть, що$n \perp m$.

Частина «Якщо». Припустимо$n$, це загальний перпендикуляр. Позначимо по$L$ і$M$ його точки перетину з$\ell$ і$m$ відповідно. За лемою 12.3.1 можна припустити, що центром абсолюту$O$ є h-середина$L$ і$M$. Зверніть увагу, що в даному випадку$\ell$ є відображенням m поперек$O$ в евклідовому сенсі. Звідси випливає, що$m$ ідеальні точки h-ліній$\ell$ і симетричні один одному. Тому, якщо одна пара з них збігається, то так і інша пара. За вправою 12.1.1$\ell = m$, що суперечить припущенню$\ell \ne m$.

Пропозиція$\PageIndex{1}$

$Q$Дозволяти бути точка стопи$P$ на h-лінії$\ell$. Тоді

$PQ_h=\dfrac{1}{2} \cdot \ln \dfrac{1 + \cos \phi}{1 - \cos \phi},$

де$\phi$ - кут паралельності$P$ до$\ell$.

Зокрема, якщо$P \notin \ell$ і$\beta =|\measuredangle_h XPY|$ по якихось моментах$X,Y\in\ell$, то

$PQ_h < \dfrac{1}{2} \cdot \ln \dfrac{1+\cos \dfrac{\beta}{2}}{1- \cos \dfrac{\beta}{2}}.$

$2021-02-24 пнг$

Доказ

Застосовуючи рух h-площини при необхідності, ми можемо припустити, що$P$ це центр абсолюту. Потім h-лінії через$P$ є перетинами евклідових ліній з h-площиною.

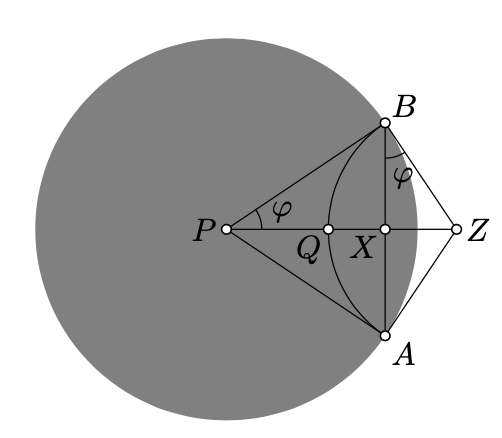
Нехай$A$ і$B$ позначають ідеальні точки$\ell$. Без втрати спільності можна вважати, що$\angle APB$ це позитивно. В даному випадку

$\phi=\measuredangle QPB=\measuredangle APQ=\dfrac{1}{2} \cdot\measuredangle APB.$

$Z$Дозволяти бути центром кола,$\Gamma$ що містить h-лінію$\ell$. $X$Встановити точку перетину евклідового відрізка$[AB]$ і лінії$(PQ)$.

Зверніть увагу, що,$PX = \cos \phi$. Тому, за Леммою 12.3.2,

$PX_h=\ln \dfrac{1+\cos\phi}{1-\cos\phi}.$

Зверніть увагу, що обидва кути$PBZ$ і$BXZ$ правильні. Так як кут$PZB$ спільний,$\triangle ZBX \sim \triangle ZPB$. Зокрема,

$ZX \cdot ZP = ZB^2;\]$

тобто$X$ є зворотним$P$ в$\Gamma$.

Інверсія в$\Gamma$ є відображенням h-площини поперек$\ell$. Тому

$\begin{array} {rcl} {PQ_h} & = & {QX_h =} \\ {} & = & {\dfrac{1}{2} \cdot PX_h =} \\ {} & = & {\dfrac{1}{2} \cdot \ln \dfrac{1 + \cos \phi}{1 - \cos \phi}.} \end{array}$

Останній оператор слідує$\phi > \dfrac{\beta}{2}$ since і функція

зменшується в інтервалі$(0,\dfrac{\pi}{2}]$.

Вправа$\PageIndex{2}$

$ABC$Дозволяти рівносторонній h-трикутник зі стороною$100$. Покажіть, що

$|\measuredangle_h ABC|<\frac1{10\ 000\ 000\ 000}.$

Підказка: За нерівністю трикутника h-відстань від$B$ до$(AC)_h$ становить не менше 50. Залишилося прикинути$|\measuredangle_h ABC| using Proposition \(\PageIndex{1}$. Нерівність$\cos \phi \le 1 - \dfrac{1}{10} \cdot \phi^2$ для$|\phi| < \dfrac{\pi}{2}$ і$e^3 > 10$ повинна допомогти закінчити докази.

Вправа\(\PageIndex{1}\)

Пропозиція\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)