13.5: Конформна інтерпретація

Last updated
Save as PDF

Page ID: 58981

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Наведемо ще одне тлумачення h-відстані.

Лемма$\PageIndex{1}$

Розглянемо h-площину з одиничною окружністю в центрі$O$ як абсолютну. Закріпіть точку$P$ і нехай$Q$ буде ще одна точка в h-площині. Набір$x = PQ$ і$y = PQ_h$. Тоді

\[\lim_{x\to 0} \dfrac{y}{x} = \dfrac{2}{1-OP^2}.\]

Наведена вище формула говорить нам, що h-відстань від$P$ до$Q$ сусідньої точки майже пропорційна евклідовій відстані з коефіцієнтом$\dfrac{2}{1-OP^2}$. Значення$\lambda(P)=\dfrac{2}{1-OP^2}$ називається конформним коефіцієнтом h-метрики.

Значення$\dfrac{1}{\lambda(P)}=\dfrac{1}{2} \cdot (1-OP^2)$ можна інтерпретувати як обмеження швидкості в заданій точці$P$. У цьому випадку h-відстань - це мінімальний час, необхідний для подорожі від однієї точки h-площини до іншої точки.

$2021-02-24 пл.$

Доказ

Якщо$P=O$, то згідно з Леммою 12.3.2

\[\dfrac{y}{x}=\dfrac{\ln \dfrac{1+x}{1-x}}{x}\to 2\]

як$x\to0$.

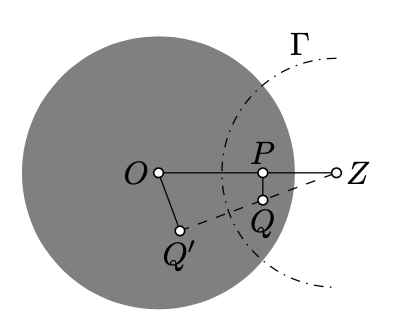
Якщо$P\ne O$, нехай$Z$ позначає обернене$P$ в абсолюті. Припустимо, що$\Gamma$ позначає коло з центром,$Z$ перпендикулярним абсолюту.

Згідно з основним спостереженням (теорема 12.3.1) і лема 12.3.1, інверсія в$\Gamma$ - це рух h-площині, яка посилає$P$ на$O$. Зокрема, якщо$Q'$ позначає зворотне$Q$ в$\Gamma$, то$OQ'_h=PQ_h$.

Набір$x'=OQ'$. Згідно з Леммою 10.1.1,

$\dfrac{x'}{x}=\dfrac{OZ}{ZQ}.$

Оскільки$Z$ є зворотним$P$ в абсолюті, ми маємо це$PO\cdot OZ=1$. Тому,

як$x \to 0$.

Згідно з 13.5.1,$\dfrac{y}{x'} \to 2$ як$x' \to 0$. Тому

як$x \to 0$.

Ось застосування леми вище.

Пропозиція$\PageIndex{1}$

Окружність h-кола h-радіуса$r$ дорівнює

$2 \cdot \pi \cdot \sinh r,$

де$\sinh r$ позначає гіперболічний синус$r$; тобто,

$\sinh r := \dfrac{e^r-e^{-r}}{2}.$

Перш ніж ми продовжимо доказ, обговоримо ту ж проблему в евклідовій площині.

Окружність кола в евклідовій площині може бути визначена як межа периметрів правильних$n$ -кутників, вписаних в коло як$n \to \infty$.

А саме зафіксуємо$r>0$. Задано натуральне число$n$, розглянемо$\triangle AOB$ таке, що$\measuredangle AOB=\dfrac{2\cdot\pi}{n}$ і$OA=OB=r$. Набір$x_n=AB$. Зверніть увагу, що$x_n$ це сторона правильного$n$ -кутника, вписаного в коло радіуса$r$. Тому периметр$n$ -кутника є$n\cdot x_n$.

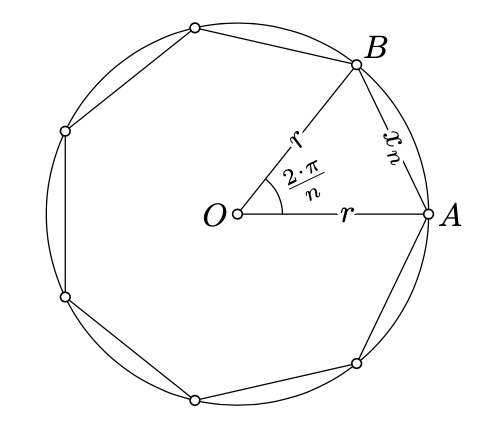
$2021-02-25 пнг$

Окружність кола з радіусом$r$ може бути визначена як межа

\[\lim_{n\to\infty} n\cdot x_n=2\cdot\pi\cdot r.\]

(Ця межа може бути прийнята як визначення$\pi$.)

У наступному доказі повторюємо ту ж конструкцію в h-площині.

Доказ

Без втрати спільності можна вважати, що центр$O$ кола є центром абсолюту.

За лемою 12.3.2 h-коло з h-радіусом$r$ є евклідове коло з центром$O$ і радіусом

$a=\dfrac{e^r-1}{e^r+1}.$

Нехай$x_n$ і$y_n$ позначають довжини сторін правильних$n$ -кутників, вписаних в коло в евклідовій і гіперболічній площині відповідно.

Зверніть увагу, що$x_n\to0$ як$n\to\infty$. За Лемма$\PageIndecx{1}$,

$\lim_{n\to\infty} \dfrac{y_n}{x_n} = \dfrac{2}{1-a^2}.$

Застосовуючи 13.5.2, отримуємо, що окружність h-кола можна знайти наступним чином:

$\begin{array} {rcl} {\lim_{n \to \infty} n \cdot y_n} & = & {\dfrac{2}{1 - a^2} \cdot \lim_{n \to \infty} n \cdot x_n =} \\ {} & = & {\dfrac{4 \cdot \pi \cdot a}{1 - a^2} =} \\ {} & = & {\dfrac{4 \cdot \pi \cdot (\dfrac{e^r - 1}{e^r + 1})}{1 - (\dfrac{e^r - 1}{e^r + 1})^2} =} \\ {} & = & {2 \cdot \pi \cdot \dfrac{e^r - e^{-r}}{2} =} \\ {} & = & {2 \cdot \pi \cdot \sinh r.} \end{array}$

Вправа$\PageIndex{1}$

$\circum_h(r)$Дозволяти позначити окружність h-кола h-радіуса$r$. Покажіть, що

\ (\\ текст {коло} _h (r+1) >2\ cdot\ текст {коло} _h (r)\])

для всіх$r>0$.

Підказка: Застосувати пропозицію$\PageIndex{1}$. Використовуйте це$e > 2$ і, зокрема, функція$r \mapsto e^{-r}$ зменшується.

Лемма\(\PageIndex{1}\)

Пропозиція\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)