13.4: Гіперболічні трикутники

Last updated
Save as PDF

Page ID: 58972

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Теорема$\PageIndex{1}$

Будь-який невироджений гіперболічний трикутник має позитивний дефект.

Доказ

Закріпіть h-трикутник$ABC$. Відповідно до теореми 11.3.1

\[\text{defect}(\triangle_hABC)\ge 0\]

Залишається показати, що в разі рівності$\triangle_hABC$ вироджується.

Без втрати спільності, ми можемо припустити, що$A$ це центр абсолюту; в даному випадку$\measuredangle_h CAB = \measuredangle CAB$. Тим не менш, ми можемо припустити, що

$\measuredangle_h CAB$,$\measuredangle_h ABC$,$\measuredangle_h BCA$,$ \measuredangle ABC$,$\measuredangle BCA \ge 0.$

$D$Дозволяти бути довільною точкою в$[CB]_h$ відмінному від$B$ і$C$. З пропозиції 9.6.1 ми маємо

$\measuredangle ABC-\measuredangle_h ABC \equiv \pi-\measuredangle CDB \equiv \measuredangle BCA-\measuredangle_h BCA.$

З вправи 7.4.2 ми отримуємо, що

Тому, якщо ми маємо рівність в 13.4.1, то$\measuredangle CDB=\pi$. Зокрема, h-сегмент$[BC]_h$ збігається з евклідовим сегментом$[BC]$. За вправою 12.1.3 останнє може статися тільки в тому випадку, якщо h-лінія$(BC)_h$ проходить через центр абсолюту ($A$); тобто якщо$\triangle_hABC$ вироджується.

Наступна теорема стверджує, зокрема, що невироджені гіперболічні трикутники є конгруентними, якщо їх відповідні кути рівні. Зокрема, в гіперболічної геометрії подібні трикутники повинні бути конгруентними.

Теорема$\PageIndex{2}$ AAA congruence condition

Два невироджених h-трикутника$ABC$ і$A'B'C'$ є конгруентними if$\measuredangle_hABC = \pm \measuredangle_hA'B'C'$,$\measuredangle_hBCA = \pm \measuredangle_h B'C'A'$ і$\measuredangle_hCAB = \pm \measuredangle_hC'A'B'$.

Доказ

Зверніть увагу, що якщо$AB_h=A'B'_h$, то теорема випливає з ASA.

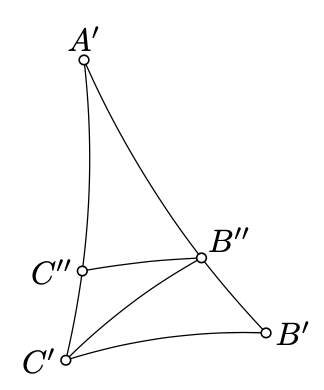
$2021-02-24 пнг$

Припустимо, навпаки. Без втрати спільності ми можемо припустити, що$AB_h<A'B'_h$. Тому ми можемо вибрати точку$B''\in [A'B']_h$ таку, що$A'B''_h=AB_h$.

Вибираємо h-полустрочку$[B''X)$ так, щоб

$\measuredangle_h A'B''X=\measuredangle_h A'B'C'.$

Згідно з вправою 11.5,$(B''X)_h\parallel(B'C')_h$.

За теоремою Паша (теорема 3.12),$(B''X)_h$ перетинається$[A'C']_h$. Припустимо, що$C''$ позначає точку перетину.

За даними$\triangle_h ABC\cong\triangle_h A'B''C''$ ASA, зокрема,

\[\text{defect}(\triangle_h ABC)=\text{defect}(\triangle_h A'B''C'').\]

Застосовуючи вправу 11.11 двічі, отримуємо, що

\[\begin{array} {rcl} {\text{defect} (\triangle_h A'B'C')} & = & {\text{defect} (\triangle_h A'B''C'') +} \\ {} & + & {\text{defect}(\triangle_h B''C''C') + \text{defect} (\triangle_h B''C'B').} \end{array}\]

За теоремою 13.7 всі дефекти повинні бути позитивними. Тому

$\text{defect} (\triangle_h A'B'C') > \text{defect} (\triangle_h ABC).$

З іншого боку,

$\begin{array} {rcl} {\text{defect} (\triangle_h A'B'C')} & = & {|\measuredangle_h A'B'C'| + |\measuredangle_h B'C'A'| + |\measuredangle_h C'A'B'| =} \\ {} & = & {|\measuredangle_h ABC| + |\measuredangle_BCA| + |\measuredangle_h CAB|} \\ {} & = & {\text{defect} (\triangle_h ABC)} \end{array}$

— протиріччя.

Нагадаємо, що біекція від h-площини до себе називається збереженням кута, якщо

$\measuredangle_h ABC= \measuredangle_h A'B'C'$

для будь-якого$\triangle_h ABC$ і свого образу$\triangle_h A'B'C'$.

Вправа$\PageIndex{1}$

Показати, що будь-яке перетворення h-площини, що зберігає кут, є рухом.

Підказка: Застосувати умову AAA-конгруентності (теорема$\PageIndex{2}$)

Теорема\(\PageIndex{1}\)

Теорема\(\PageIndex{2}\) AAA congruence condition

Вправа\(\PageIndex{1}\)