12.9: Гіперболічна тригонометрія

Last updated
Save as PDF

Page ID: 59010

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми наведемо формули для h-відстані за допомогою гіперболічних функцій. Одна з цих формул буде використана в доведенні гіперболічної теореми Піфагора (Теорема 13.6.1).

Нагадаємо$\cosh$, що$\sinh$, і$\tanh$ позначають гіперболічний косинус, гіперболічний синус і гіперболічний тангенс; тобто функції, визначені

$\cosh x := \dfrac{e^x + e^{-x}}{2}$,$\sinh x := \dfrac{e^x - e^{-x}}{2}$,

$\tanh x := \dfrac{\sinh x}{\cosh x}.$

Ці гіперболічні функції аналогічні синусу і косинусу і тангенсу.

Вправа$\PageIndex{1}$

Доведіть такі ідентичності:

$\cosh' x=\sinh x$$\sinh'x=\cosh x$;$(\cosh x)^2-(\sinh x)^2=1.$

Теорема$\PageIndex{1}$ Double-argument identities

тотожності

$\cosh (2 \cdot x) = (\cosh x)^2 + (\sinh x)^2$і$\sinh (2 \cdot x) = 2 \cdot \sinh x \cdot \cosh x$

утримувати для будь-якої реальної вартості$x$.

Доказ

$\begin{array} {rcl} {(\sinh x)^2 + (\cosh x)^2} & = & {(\dfrac{e^x - e^{-x}}{2})^2 + (\dfrac{e^x + e^{-x}}{2})^2 =} \\ {} & = & {\dfrac{e^{2 \cdot x} + e^{-2 \cdot x}}{2} =} \\ {} & = & {\cosh (2 \cdot x);} \end{array}$

$\begin{array} {rcl} {2 \cdot \sinh x \cdot cosh x} & = & {2 \cdot (\dfrac{e^x - e^{-x}}{2}) \cdot (\dfrac{e^x + e^{-x}}{2})} \\ {} & = & {\dfrac{e^{2 \cdot x} - e^{-2 \cdot x}}{2}} \\ {} & = & {\cosh (2 \cdot x).} \end{array}$

Розширені вправи$\PageIndex{2}$

$P$$Q$Дозволяти і бути два h-точки відмінні від центру абсолюту. $Q'$Позначають$P'$ і зворотні від$P$ і$Q$ в абсолюті.

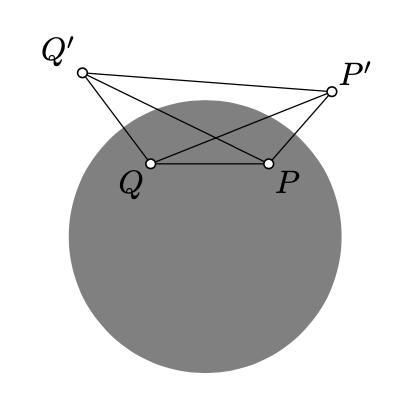
$2021-02-24 пнг$

(а)$\cosh [\dfrac{1}{2} \cdot PQ_h] = \sqrt{\dfrac{PQ' \cdot P'Q}{PP' \cdot QQ'}};$

(б)$\sinh [\dfrac{1}{2} \cdot PQ_h] = \sqrt{\dfrac{PQ \cdot P'Q'}{PP' \cdot QQ'}};$

(c)$\tanh [\dfrac{1}{2} \cdot PQ_h] = \sqrt{\dfrac{PQ \cdot P'Q'}{PQ' \cdot P'Q}};$

(г)$\cosh PQ_h = \dfrac{PQ \cdot P'Q' + PQ' \cdot P'Q}{PP' \cdot QQ'}$.

Підказка

За слідством 10.6.1 та теореми 10.2.1 праві сторони в тотожності виживають під інверсією в колі, перпендикулярному абсолюту.

Як завжди, ми припускаємо, що абсолют - це одиничне коло. Припустимо, що$O$ позначає h-середину$[PQ]_h$. За основним спостереженням (теорема 12.3.1) можна припустити, що$O$ є центром абсолюту. У цьому$O$ випадку також евклідова середина$[P Q]$. (Замість цього ми можемо$Q$ перейти до центру абсолюту. В цьому випадку похідні простіше. Але з тих пір$Q'Q = Q'P = QP = \infty$, треба виправдовувати це$\dfrac{\infty}{\infty} = 1$ кожен раз.)

Встановити$a = OP = OQ$; в цьому випадку у нас є

$\begin{array} {rcl} {PQ} & = & {2 \cdot a,} \\ {P'Q'} & = & {2 \cdot \dfrac{1}{a},} \end{array}$$\begin{array} {l} {PP' = QQ' = \dfrac{1}{a} - a,} \\ {PQ' = QP' = \dfrac{1}{a} + a.} \end{array}$

$PQ_h = \ln \dfrac{(1 + a)^2}{(1 - a)^2} = 2 \cdot \ln \dfrac{1 + a}{1 - a}.$

Тому

$\begin{array} {rcl} {\cosh [\dfrac{1}{2} \cdot PQ_h]} & = & {\dfrac{1}{2} \cdot (\dfrac{1 + a}{1 - a} + \dfrac{1 - a}{1 + a})=} \\ {} & = & {\dfrac{1 + a^2}{1 - a^2};} \end{array}$$\begin{array} {rcl} {\sqrt{\dfrac{PQ' \cdot P'Q}{PP' \cdot QQ'}}} & = & {\dfrac{\dfrac{1}{a} + a}{\dfrac{1}{a} - a} =} \\ {} & = & {\dfrac{1 + a^2}{1 - a^2}.} \end{array}$

Звідси випливає частина (а). Аналогічно,

$\begin{array} {rcl} {\sinh [\dfrac{1}{2} \cdot PQ_h]} & = & {\dfrac{1}{2} \cdot (\dfrac{1 + a}{1 - a} - \dfrac{1 - a}{1 + a}) =} \\ {} & = & {\dfrac{2 \cdot a}{1 - a^2};} \end{array}$$\begin{array} {rcl} {\sqrt{\dfrac{PQ \cdot P'Q'}{PP' \cdot QQ'}}} & = & {\dfrac{2}{\dfrac{1}{a} - a} =} \\ {} & = & {\dfrac{2 \cdot a}{1 - a^2}.} \end{array}$

Звідси випливає частина (b).

Частини (c) і (d) випливають з (a), (b), визначення гіперболічного тангенса та ідентичності з подвійним аргументом для гіперболічного косинуса, див. Теорема$\PageIndex{1}$.

Вправа\(\PageIndex{1}\)

Теорема\(\PageIndex{1}\) Double-argument identities

Розширені вправи\(\PageIndex{2}\)