10.1: Інверсія

Last updated
Save as PDF

Page ID: 59077

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

$\Omega$Дозволяти коло з центром$O$ і радіусом$r$. Інверсія точки$P$ в$\Omega$ - це точка$P' \in [OP)$ така, що

$OP \cdot OP' = r^2.$

У цьому випадку коло$\Omega$ буде називатися колом інверсії, а його центр$O$ називається центром інверсії.

$O$Зворотне не визначено.

Зверніть увагу$\Omega$, що якщо$P$$P'$ знаходиться всередині, то зовні і навпаки. Далі,$P = P'$ якщо і тільки якщо$P \in \Omega$.

Зверніть увагу, що інверсія$P'$ відображає назад до$P$.

Вправа$\PageIndex{1}$

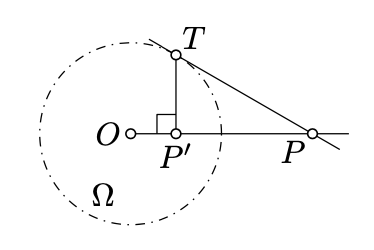
$\Omega$Дозволяти бути коло по центру$O$. Припустимо,$(PT)$ що лінія дотична до$\Omega$ at$T$. $P'$Дозволяти бути точкою стопи$T$ на$(OP)$.

Покажіть, що$P'$ є зворотним від$P$ in$\Omega$.

$2021-02-19 г$

Підказка: За Лемма 5.6.2,$\angle OTP'$ це правильно. Тому,$\triangle OPT \sim \triangle OTP'$ а зокрема$OP \cdot OP' = OT^2$ і звідси і результат.

Лемма$\PageIndex{1}$

$\Gamma$Дозволяти буде коло з центром$O$. Припустимо$A'$ і$B'$ є оберненнями$A$ і$B$ в$\Gamma$. Тоді

$\triangle OAB \sim \triangle OB'A'.$

Більше того

\[\begin{array} {rcl} {\measuredangle AOB} & \equiv & {-\measuredangle B'OA',} \\ {\measuredangle OBA} & \equiv & {-\measuredangle OA'B',} \\ {\measuredangle BAO} & \equiv & {-\measuredangle A'B'O.} \end{array}\]

Доказ

$r$Дозволяти радіус кола інверсії.

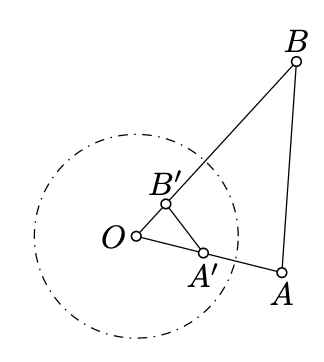
$2021-02-19 пнг$

За визначенням інверсії,

$OA \cdot OA' = OB \cdot OB' = r^2.$

Тому,

$\dfrac{OA}{OB'} = \dfrac{OB}{OA'}.$

Зрозуміло,

$\measuredangle AOB = \measuredangle A'OB' \equiv -\measuredangle B'OA'.$

З SAS ми отримуємо, що

$\triangle OAB \sim \triangle OB'A'.$

Застосовуючи теореми 3.3.1 і 10.1.2, отримаємо 10.1.1.

Вправа$\PageIndex{2}$

$P'$Дозволяти бути зворотним$P$ в колі$\Gamma$. Припустимо, що$P \ne P'$. Показати,$\dfrac{PX}{P'X}$ що значення однакове для всіх$X \in \Gamma$.

Зворотне до вправи вище також тримає. А саме, задано додатне дійсне число$k \ne 1$ та дві різні точки$P$ та$P'$ місце розташування точок,$X$ таких, що$\dfrac{PX}{P'X} = k$ утворює коло, яке називається аполлонівським колом. В даному випадку$P'$ є зворотним$P$ в аполлонському колі.

Підказка

Припустимо, що$O$ позначає центр$\Gamma$. Припустимо, що$X, Y \in \Gamma$; зокрема,$OX = OY$.

Зверніть увагу, що інверсія посилає$X$ і$Y$ до себе. За Лемма$\PageIndex{1}$,

$\triangle OPX \sim \triangle OXP'$і$\triangle OPY \sim \triangle OYP'$.

Тому,$\dfrac{PX}{P'X} = \dfrac{OP}{OX} = \dfrac{OP}{OY} = \dfrac{PY}{P'Y}$ а значить і результат.

Вправа$\PageIndex{3}$

Нехай$A',B'$, і$C'$ бути зображення$A,B$, і$C$ під інверсією в окружності$\triangle ABC$. Показати, що incenter$\triangle ABC$ є ортоцентром$\triangle A'B'C'$.

Підказка

За Лемма$\PageIndex{1}$,

$\measuredangle IA'B' \equiv -\measuredangle IBA$,$\measuredangle IB'C' \equiv -\measuredangle ICB$$\measuredangle IC'A' \equiv -\measuredangle IAC$,
$\measuredangle IB'A' \equiv -\measuredangle IAB$,$\measuredangle IC'B' \equiv -\measuredangle IBC$,$\measuredangle IA'C' \equiv -\measuredangle ICA$.

Залишилося застосувати теорему про суму кутів трикутника (Теорема 7.4.1), щоб показати$(A'I) \perp (B'C')$, що,$(B'I) \perp (C'A')$ і$(C'I) \perp (B'A')$.

Вправа$\PageIndex{4}$

Складіть лінійку і компас побудови оберненої заданої точки в заданому колі.

Підказка

Вгадайте конструкцію з діаграми (дві непересічні лінії на схемі паралельні).

$2021-02-19 пл.$

Вправа\(\PageIndex{1}\)

Лемма\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)