10.5: Перпендикулярні кола

Last updated
Save as PDF

Page ID: 59084

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Припустимо два кола$\Gamma$ і$\Omega$ перетинаються в двох точках$X$ і$Y$. $\ell$$m$Дозволяти і бути дотичними лініями в$X$ до$\Gamma$ і$\Omega$ відповідно. Аналогічно,$\ell'$ і$m'$ бути дотичними лініями від$Y$ до$\Gamma$ і$\Omega$.

З вправи 9.6.3 ми отримуємо, що$\ell \perp m$ якщо і тільки якщо$\ell' \perp m'$.

Ми говоримо,$\Gamma$ що коло перпендикулярна колу$\Omega$ (коротко$\Gamma \perp \Omega$), якщо вони перетинаються і лінії, дотичні до кіл в одній точці (а значить, обидві точки) перетину перпендикулярні.

Аналогічно ми говоримо,$\Gamma$ що коло перпендикулярно до прямої$\ell$ (коротко$\Gamma \perp \ell$) якщо$\Gamma \cap \ell \ne \emptyset$ і$\ell$ перпендикулярно дотичним лініям до$\Gamma$ однієї точки (а отже, і обох точок) перетину. Згідно з Леммою 5.6.2, це відбувається тільки в тому випадку, якщо лінія l проходить через центр$\Gamma$.

Тепер можна говорити про перпендикулярних колах.

Теорема$\PageIndex{1}$

Припустимо$\Gamma$ і$Omega$ є окремими колами. Тоді$\Omega \perp \Gamma$ якщо і тільки якщо коло$\Gamma$ збігається з його інверсією в$\Omega$.

Доказ

Припустимо, що$\Gamma'$ позначає зворотне$\Gamma$.

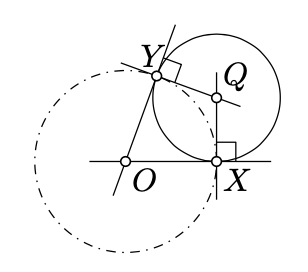
$2021-02-22 11.09.06.пнг$

«Тільки якщо» частина. $O$Дозволяти бути центром$\Omega$ і$Q$ бути центром$\Gamma$. Нехай$X$ і$Y$ позначають точки перетинів$\Gamma$ і$Omega$. Відповідно до Лемми 5.6.2,$\Omega \perp \Gamma$ якщо і тільки якщо$(OX)$ і$(OY)$ дотичні до$\Gamma$.

Зверніть увагу, що також$\Gamma'$ є$(OX)$ дотичною до$(OY)$ і$X$ і$Y$ відповідно. Звідси випливає, що$X$ і$Y$ є точками стопи центру$\Gamma'$ на$(OX)$ і$(OY)$. Тому обидва$\Gamma'$ і$\Gamma$ мають центр$Q$. Нарешті$\Gamma' = \Gamma$, так як обидва кола проходять через$X$.

Частина «Якщо». Припустимо$\Gamma = \Gamma'$.

Так як$\Gamma \ne \Omega$, є момент$P$, який лежить на$\Gamma$, але не на$\Omega$. $P'$Дозволяти бути зворотним$P$ в$\Omega$. З тих пір$\Gamma = \Gamma'$, у нас це є$P' \in \Gamma$. Зокрема, напівлінія$[OP)$ перетинається$\Gamma$ в двох точках. За вправою 5.6.1$O$ лежить за межами$\Gamma$.

Як$\Gamma$ має точки всередині і зовні$\Omega$, кола$\Gamma$ і$\Omega$ перетинаються. Останнє випливає з вправи 3.5.1.

$X$Дозволяти точка їх перетину. Нам потрібно показати, що$(OX)$ є$\Gamma$ дотичною до;$X$ тобто єдина точка перетину$(OX)$ і$\Gamma$.

Припустимо$Z$, це ще одна точка перетину. Так як$O$ знаходиться зовні$\Gamma$, точка$Z$ лежить на півлінії$[OX)$.

Припустимо, що$Z'$ позначає зворотне$Z$ in$\Omega$. Зрозуміло, що три пункти$Z$$Z'$,$X$ лежать на$\Gamma$ і$(OX)$. Останнє суперечить Леммі 5.6.1.

Зручно визначити інверсію в лінії$\ell$ як відображення поперек$\ell$. Таким чином ми можемо говорити про інверсії в довільному колі.

Слідство$\PageIndex{1}$

$\Omega$$\Gamma$Дозволяти і бути різні кола в зворотній площині. Потім інверсія в$\Omega$ посилає$\Gamma$ собі якщо і тільки якщо$\Omega \perp \Gamma$.

Доказ

За Thorem досить розглянути випадок$\PageIndex{1}$, коли$\Omega$ або$\Gamma$ є лінією.

Припустимо,$\Omega$ це лінія, тому інверсія в$\Omega$ є відображенням. У цьому випадку твердження випливає з Слідство 5.4.1.

Якщо$\Gamma$ рядок, то твердження випливає з теореми 10.3.2.

Слідство$\PageIndex{2}$

$P$$P'$Дозволяти і бути дві різні точки такі, що$P'$ є оберненою$P$ в колі$\Omega$. Припустимо, що лінія кола$\Gamma$ проходить через$P$ і$P'$. Потім$\Gamma \perp \Omega$.

Доказ

Без втрати спільності можна вважати, що$P$ знаходиться всередині і$P'$ знаходиться зовні$\Omega$. За теоремою 3.5.1,$\Gamma$ перетинається$\Omega$. Припустимо, що А позначає точку перетину.

Припустимо, що$\Gamma'$ позначає зворотне$\Gamma$. Оскільки$A$ є самооберненою$A, P$, точки і$P'$ лежать далі$\Gamma'$. За вправою 8.1.1,$\Gamma'$ =$\Gamma$ і по теоремі$\PageIndex{1}$,$\Gamma \perp \Omega$.

Слідство$\PageIndex{3}$

$P$$Q$Дозволяти і бути дві різні точки всередині кола$\Omega$. Потім існує унікальна лінія кола,$\Gamma$ перпендикулярна до$\Omega$ якої проходить через$P$ і$Q$.

Доказ

$P'$Дозволяти бути зворотною точки$P$ в колі$\Omega$. Відповідно до$\PageIndex{2}$ Слідство, лінія кола проходить через$P$ і$Q$ перпендикулярна$\Omega$ якщо і тільки якщо вона проходить через$P'$.

Зверніть увагу, що$P'$ лежить за межами$\Omega$. Тому точки$P$$P'$, і$Q$ розрізняються.

Відповідно до вправи 8.1.1, існує унікальна лінія кола, що проходить через$P, Q$, і$P'$. Звідси і результат.

Вправа$\PageIndex{1}$

Дозволяти$P, Q, P'$, і$Q'$ бути точки в евклідовій площині. Припустимо$P'$ і$Q'$ є оберненнями$P$ і$Q$ відповідно. Покажіть, що чотирикутник$PQP'Q'$ вписаний.

Підказка: Застосовуйте теорему 10.2.1, теорему 7.4.5 та теорему 9.2.1.

Вправа$\PageIndex{2}$

$\Omega_2$Дозволяти$\Omega_1$ і бути два перпендикулярних кіл з центрами в$O_1$ і$O_2$ відповідно. Показати, що зворотне$O_1$ в$\Omega_2$ збігається з оберненим$O_2$ in$\Omega_1$.

Підказка: Припустимо, що$T$ позначає точку перетину$\Omega_1$ і$\Omega_2$. $P$Дозволяти бути точкою стопи$T$ на$(O_1O_2)$. Покажіть, що$\triangle O_1PT \sim \triangle O_1TO_2 \sim \triangle TPO_2$. Вважайте, що$P$ збігається з$O_1$ оберненнями в$\Omega_2$ і$O_2$ в$\Omega_1$.

Вправа$\PageIndex{3}$

Три різних кола —$\Omega_2$ і$\Omega_1$$\Omega_3$, перетинаються в двох точках —$A$ і$B$. Припустимо,$\Gamma$ що коло перпендикулярно$\Omega_1$ і$\Omega_2$. Покажіть, що$\Gamma \perp \Omega_3$.

Підказка: Так як$\Gamma \perp \Omega_1$ і$\Gamma \perp \Omega_2$, Слідство$PageIndex{1}$ має на увазі, що кола$\Omega_1$ і$\Omega_2$ перевернуті$\Gamma$ в себе. Зробіть висновок, що точки$A$ і$B$ є зворотними один одному. Оскільки$\Omega_3 \ni A, B$, Слідство$\PageIndex{2}$ має на увазі, що$\Omega_3 \perp \Gamma$.

Розглянемо два нових інструменти побудови: інструмент circumtool, який будує лінію кола через три задані точки, і інструмент інверсії-інструмент — інструмент, який будує обернену задану точку в заданій лінії кола.

Вправа$\PageIndex{4}$

Враховуючи два кола$\Omega_2$ та точку$\Omega_1$,$P$ яка не лежить на колах, використовуйте лише інструмент кругового та інверсійного інструменту для побудови лінії кола,$\Gamma$ яка проходить через$P$, і перпендикулярна обом$\Omega_1$ і$\Omega_2$.

Підказка

Нехай$P_1$ і$P_2$ бути зворотним$P$ в$\Omega_1$ і$\Omega_2$. Застосуйте$\PageIndex{2}$ Слідство та Теорему,$\PageIndex{1}$ щоб показати$\Gamma$, що коло, що проходить через

$P, P_1$, і$P_3$ є рішенням.

Розширені вправи$\PageIndex{5}$

Дано три нероз'ємні кола$\Omega_1$,$\Omega_2$ і$\Omega_3$, використовувати тільки циркулярний інструмент і інверсія-інструмент для побудови лінії кола$\Omega_1$,$\Gamma$ яка перпендикулярна кожному колу,$\Omega_2$ і$\Omega_3$.

Подумайте, що робити, якщо два кола перетинаються.

Підказка

Всі кола, які перпендикулярно$\Omega_1$ і$\Omega_2$ проходять через фіксовану точку$P$. Спробуйте побудувати$P$.

Якщо два кола перетинаються, спробуйте застосувати Слідство 10.6.1.

Теорема\(\PageIndex{1}\)

Слідство\(\PageIndex{1}\)

Слідство\(\PageIndex{2}\)

Слідство\(\PageIndex{3}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)

Розширені вправи\(\PageIndex{5}\)