10.6: Кути після інверсії

Last updated
Save as PDF

Page ID: 59091

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Пропозиція$\PageIndex{1}$

У зворотній площині зворотна дуга - це дуга.

Доказ

Розглянемо чотири різні точки$A, B, C$, і$D$; нехай$A', B', C'$, і$D'$ бути їх зворотними. Потрібно показати, що$D$ лежить на дузі тоді і тільки$ABC$ тоді, коли$D'$ лежить на дузі$A'B'C'$. Відповідно до Пропозиції 9.5.1, останнє еквівалентно наступному:

$\measuredangle ADC = \measuredangle ABC \Leftrightarrow \measuredangle A'D'C' = \measuredangle A'B'C'.$

Останнє випливає з теореми 10.2.1b.

Наступна теорема стверджує, що кут між дугами змінює тільки свій знак після інверсії.

Теорема$\PageIndex{1}$

$AB_1C_1$$AB_2C_2$Дозволяти, бути дві дуги в зворотній площині, і дуги$A'B_1'C_1'$,$A'B_2'C_2'$ бути їх зворотні. $[AX_1)$$[AX_2)$Дозволяти і бути напівлінії дотичні до$AB_1C_1$ і$AB_2C_2$ в$A$,$[A'Y_1)$ і$[A'Y_2)$ бути половиною лінії дотичні до$A'B_1'C_1'$ і$A'B_2'C_2'$ в$A'$. Тоді

$\measuredangle X_1AX_2 \equiv -\measuredangle Y_1A'Y_2$.

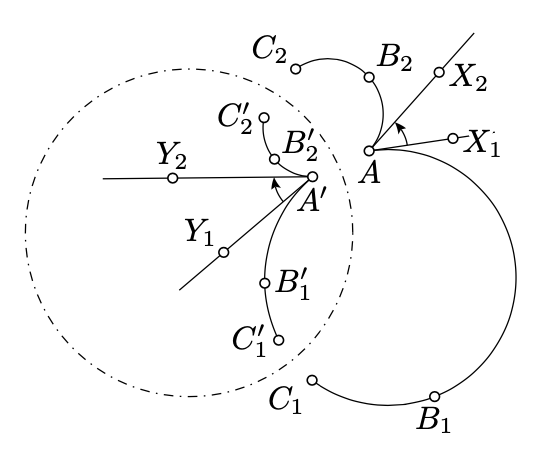
$2021-02-22 пнг$

Доказ

Застосувавши до Пропозиції 9.6.1,

$\begin{array} {rcl} {\measuredangle X_1AX_2} & \equiv & {\measuredangle X_1AC_1 + \measuredangle C_1AC_2 + \measuredangle C_2AX_2 \equiv} \\ {} & \equiv & {(\pi - \measuredangle C_1B_1A) + \measuredangle C_1AC_2 + (\pi - \measuredangle AB_2C_2) \equiv} \\ {} & \equiv & {-(\measuredangle C_1B_1A + \measuredangle AB_2C_2 + \measuredangle C_2AC_1) \equiv} \\ {} & \equiv & {-(\measuredangle C_1B_1A + \measuredangle AB_2C_1) -(\measuredangle C_1B_2C_2 + \measuredangle C_2AC_1).} \end{array}$

Так само ми отримуємо, що

$\measuredangle Y_1A'Y_2 \equiv -(\measuredangle C_1'B_1'A' + \measuredangle A'B_2'C_1') - (\measuredangle C_1'B_2'C_2' + \measuredangle C_2'A'C_1').$

За теоремою 10.2.1b,

$\begin{array} {rcl} {\measuredangle C_1B_1A + \measuredangle AB_2C_1} & \equiv & {-(\measuredangle C_1'B_1'A' + \measuredangle A'B_2'C_1'),} \\ {\measuredangle C_1B_2C_2 + \measuredangle C_2AC_1} & \equiv & {-(\measuredangle C_1'B_2'C_2' + \measuredangle C_2'A'C_1')} \end{array}$.

а значить і результат.

Кут між дугами можна визначити як кут між його дотичними півлініями в загальній кінцевій точці. Тому при інверсії кути між дугами зберігаються аж до знака.

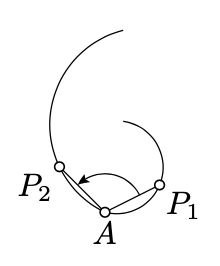
З вправи 5.7.4 випливає, що кут між дугами із загальною кінцевою точкою А - це$P_1$ межа$\measuredangle P_1AP_2$ де і$P_2$ є точками, що наближаються$A$ уздовж відповідних дуг. Це спостереження може бути використано для визначення кута між парою кривих, що виходять з однієї точки. Виходить, що при інверсії кути між кривими також зберігаються аж до знака.

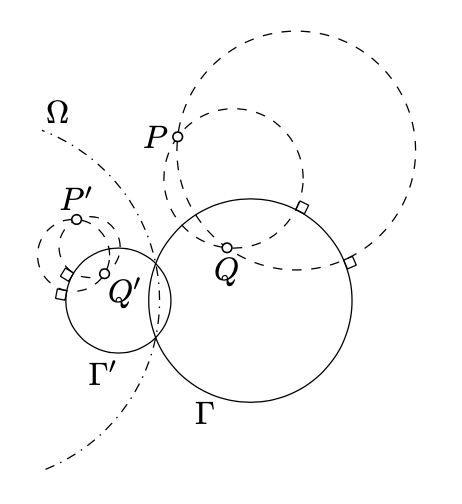
$2021-02-22 пнг$

Слідство$\PageIndex{1}$

$P$Дозволяти бути оберненою точки$Q$ в колі$\Gamma$. Припустимо$P'$$Q'$, що, і$\Gamma'$ є оберненнями$P, Q$, і$\Gamma$ в іншому колі$\Omega$. Тоді$P'$ є зворотним від$Q'$ in$\Gamma'$.

Доказ

$2021-02-22 пнг$

Якщо$P = Q$, то$P'=Q' \in \Gamma'$. Тому$P'$ є зворотним$Q'$ в$\Gamma'$.

Залишилося розглянути справу$P \ne Q$. $\Delta_2$Дозволяти$\Delta_2$ і бути два різних кола, які перетинаються в$P$ і$Q$. Згідно з наслідком 10.5.2,$\Delta_1 \perp \Gamma$ і$\Delta_2 \perp \Gamma$.

Нехай$\Delta_1'$ і$\Delta_2'$ позначають зворотні$\Delta_1$ і$\Delta_2$ в$Omega$. Зрозуміло,$\Delta_1'$ зустрічається$\Delta_2'$ при$P'$ і$Q'$.

За теоремою$\PageIndex{1}$,$\Delta_1' \perp \Gamma'$ і$\Delta_2' \perp \Gamma'$. За наслідком 10.5.1,$P'$ є зворотним$Q'$ в$\Gamma'$.

Пропозиція\(\PageIndex{1}\)

Теорема\(\PageIndex{1}\)

Слідство\(\PageIndex{1}\)