8.4: Кутові бісектриси

Last updated
Save as PDF

Page ID: 59105

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Якщо$\measuredangle ABX \equiv - \measuredangle CBX$, то ми говоримо, що лінія$(BX)$ бісекції$\angle ABC$, або лінія$(BX)$ є бісектрисою$\angle ABC$. Якщо$\measuredangle ABX \equiv \pi - \measuredangle CBX$, то лінія$(BX)$ називається зовнішньою бісектрисою$\angle ABC$.

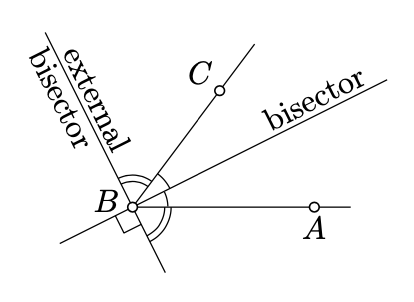
$2021-02-17 пнг$

Якщо$\measuredangle ABA' = \pi$; тобто, якщо$B$ лежить між$A$ і$A'$, то бісектриса$\angle ABC$ - це зовнішня бісектриса$\angle A'BC$ і навпаки.

Зверніть увагу, що бісектриса і зовнішня бісектриса однозначно визначаються кутом.

Вправа$\PageIndex{1}$

Покажіть, що для будь-якого кута його бісектриса і зовнішня бісектриса перпендикулярні.

Підказка

$(BX)$$(BY)$Дозволяти і бути внутрішньою і зовнішньою бісектрисами$\angle ABC$. Тоді

$2 \cdot \measuredangle XBY \equiv 2 \cdot \measuredangle XBA + 2 \cdot \measuredangle ABY \equiv \measuredangle CBA + \pi + 2 \cdot \measuredangle ABC \equiv \pi + \measuredangle CBC = \pi$

а значить і результат.

Бісектриси$\angle ABC$$\angle BCA$, і$\angle CAB$ невиродженого трикутника$ABC$ називаються бісектрисами трикутника$ABC$ у вершині$A, B$, і$C$ відповідно.

Лемма$\PageIndex{1}$

$\triangle ABC$Дозволяти бути невиродженим трикутником. Припустимо, що$A$ бісектриса у вершині перетинає сторону$[BC]$ в точці$D$. Тоді

\[\dfrac{AB}{AC} = \dfrac{DB}{DC}.\]

Доказ

$2021-02-17 пнг$

$\ell$Дозволяти лінія, що проходить через$C$, що паралельно$(AB)$. Зверніть увагу, що$\ell \nparallel (AD)$; встановити

$E = \ell \cap (AD)$.

Також зверніть увагу, що$B$ і$C$ лежать на протилежні сторони від$(AD)$. Отже, за поперечною властивістю (Теорема 7.3.1),

\[\measuredangle BAD = \measuredangle CED.\]

Далі кути$ADB$ і$EDC$ є вертикальними; зокрема, за пропозицією 2.5.1

$\measuredangle ADB = \measuredangle EDC.$

За умовою подібності АА,$\triangle ABD \sim \triangle ECD$. Зокрема,

\[\dfrac{AB}{EC} = \dfrac{DB}{DC}.\]

Оскільки$(AD)$ бісекції$\angle BAC$, ми отримуємо, що$\measuredangle BAD = \measuredangle DAC$. Разом з 8.4.2 це означає, що$\measuredangle CEA = \measuredangle EAC$. За теоремою 4.3.1,$\triangle ACE$ є рівнобедреним; тобто

$EC = AC.$

Разом з 8.4.3 він має на увазі 8.4.1.

Вправа$\PageIndex{2}$

Сформулюйте і доведіть аналог леми$\PageIndex{1}$ для зовнішньої бісектриси.

Підказка: Якщо$E$ точка перетину$(BC)$ з зовнішньою бісектрисою$\angle BAC$, то$\dfrac{AB}{AC} = \dfrac{EB}{EC}$. Це можна довести за тими ж лініями, що і Лемма$\PageIndex{1}$.

Вправа\(\PageIndex{1}\)

Лемма\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)