8.6: У центрі

Last updated
Save as PDF

Page ID: 59106

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Теорема$\PageIndex{1}$

Бісектриси кута будь-якого невиродженого трикутника перетинаються в одній точці.

Точка перетину бісектрис називається інцентром трикутника; її зазвичай позначають$I$. Точка$I$ лежить на однаковій відстані з кожного боку. Зокрема, це центр кола, дотичної до кожної сторони трикутника. Це коло називається вписаним, а його радіус називається радіусом вписання трикутника.

Доказ

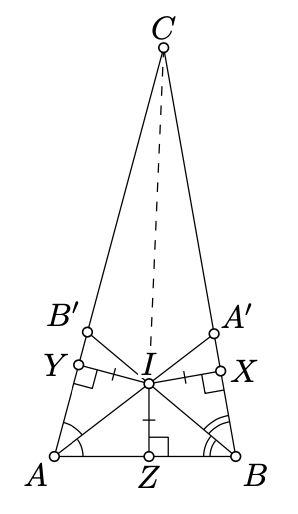
$2021-02-18 пнг$

$\triangle ABC$Дозволяти бути невиродженим трикутником.

Зверніть увагу, що точки$B$ і$C$ лежать на протилежних сторонам від бісектриси$\angle BAC$. Звідси ця бісектриса перетинається$[BC]$ в точці, скажімо$A'$.

Аналогічно є$B' \in [AC]$ таке, що$(BB')$ розсікає$\angle ABC$.

Застосовуючи теорему Паша (теорема 3.4.1) двічі для трикутників$AA'C$ і$BB'C$, отримаємо, що$[AA']$ і$[BB']$ перетинаємося. Припустимо, що$I$ позначає точку перетину.

Дозволяти$X, Y$, і$Z$ бути точки стопи$I$ на$(BC)$$(CA)$, і$(AB)$ відповідно. Застосовуючи пропозицію 8.5.1, ми отримуємо, що

$IY = IZ = IX.$

З тієї ж леми ми отримуємо, що$I$ лежить на бісектрисі або на зовнішній бісектрисі$\angle BCA$.

Лінія$(CI)$ перетинається$[BB']$, точки$B$ і$B'$ лягають на протилежні сторони від$(CI)$. Тому кути$ICB$ мають$ICB'$ і протилежні знаки. Зверніть увагу, що$\angle ICA = \angle ICB'$. Тому$(CI)$ не може бути зовнішньої бісектриси$\angle BCA$. Звідси і результат.