8.7: Більше вправ

Last updated
Save as PDF

Page ID: 59100

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Вправа$\PageIndex{1}$

Припустимо, що бісектриса кута невиродженого трикутника бісекції протилежної сторони. Покажіть, що трикутник рівнобедрений.

Підказка: Застосувати Лемма 8.4.1. Також дивіться рішення вправи 11.1.1.

Вправа$\PageIndex{2}$

Припустимо, що на одній вершині невиродженого трикутника бісектриса збігається з висотою. Покажіть, що трикутник рівнобедрений.

Підказка: Застосуйте ASA до двох трикутників, які бісектриса вирізає від початкового трикутника.

Вправа$\PageIndex{3}$

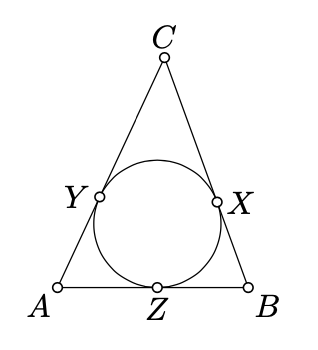
Припустимо$[BC]$$[CA]$, що сторони, і$[AB]$ з$\triangle ABC$ дотичні до вписаного кола в$X$$Y$, і$Z$ відповідно. Покажіть, що

$AY = AZ = \dfrac{1}{2} \cdot (AB + AC - BC).$

$2021-02-18 пнг$

За визначенням, вершини ортичного трикутника є базовими точками висот даного трикутника.

Підказка: $I$Дозволяти бути інцентром. За SAS, ми отримуємо це$\triangle AIZ \cong \triangle AIY$. Тому,$AY = AZ$. Таким же чином ми отримуємо, що$BX = BZ$ і$CX = CY$. Звідси і результат.

Вправа$\PageIndex{4}$

Довести, що ортоцентр гострого трикутника збігається з інцентром його ортичного трикутника.

Яким повинен бути аналог цього твердження для тупого трикутника?

Підказка

$\triangle ABC$Дозволяти заданий гострий трикутник і$\triangle A'B'C'$ бути його ортичним трикутником. Зауважте, що$\triangle AA'C \sim \triangle BB'C$. Використовуйте його, щоб показати це$\triangle A'B'C \sim \triangle ABC$.

Точно так само ми отримуємо, що$\triangle AB'C' \sim \triangle ABC$. Звідси випливає, що$\measuredangle A'B'C = \measuredangle AB'C'$. Зробіть висновок, що$(BB')$ бісекції$\angle A'B'C'$.

Якщо$\triangle ABC$ тупий, то його ортоцентр збігається з одним з екзцентрів$\triangle ABC$; тобто точка перетину двох зовнішніх і однієї внутрішньої бісектрис$\triangle ABC$.

Вправа$\PageIndex{5}$

Припустимо, що$A$$ABC$ бісектриса в трикутника перетинає сторону$[BC]$ в точці$D$; лінія через$D$ і паралельно$(CA)$ перетинається$(AB)$ в точці$E$; лінія через$E$ і паралельно$(BC)$ перетинається$(AC)$ в $F$. Покажіть, що$AE = FC$.

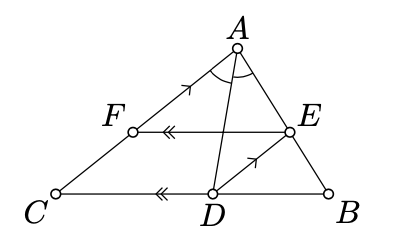
$2021-02-18 пнг$

Підказка: Застосувати теорему 4.3.1, теорему 7.3.1 та лему 7.5.1.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)

Вправа\(\PageIndex{5}\)