Skip to main content
LibreTexts - Ukrayinska

5.7: Геометричні конструкції

  1. Last updated
  2. Save as PDF
  • Page ID
    59242

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Конструкції лінійки та компаса в площині - це побудова точок, ліній та кіл, використовуючи лише ідеалізовану лінійку та циркуль. Ці будівельні завдання дають цінне джерело вправ з геометрії, які ми будемо використовувати далі в книзі. Крім того, глава 19 присвячена повністю темі.

    Ідеалізовану лінійку можна використовувати лише для того, щоб провести лінію через задані дві точки. Ідеалізований циркуль можна використовувати тільки для того, щоб намалювати коло із заданим центром і радіусом. Тобто дається три точки\(A, B\), і\(O\) ми можемо намалювати безліч всіх точок на відстані\(AB\) від\(O\). Ми також можемо позначати нові точки на площині, а також на побудованих лініях, колах та їх перетині (якщо такі точки існують).

    Ми також можемо подивитися на різні набори будівельних інструментів. Наприклад, ми можемо використовувати лише лінійку або ми можемо винайти новий інструмент, скажімо, інструмент, який створює середину для будь-яких заданих двох точок.

    Як приклад розглянемо наступну проблему:

    Теорема\(\PageIndex{1}\) Construction of midpoint

    Побудувати середню точку заданого відрізка\([AB]\).

    Будівництво.

    1. Побудувати коло з центром в\(A\) тому, що проходить через\(B\). Побудувати коло з центром в\(B\) тому, що проходить через\(A\). Відзначте обидві точки перетину цих кіл, позначте їх\(P\) і\(Q\).
    2. Намалюйте лінію\((PQ)\). Позначте точку\(M\) перетину\((PQ)\) і\([AB]\); це середина.

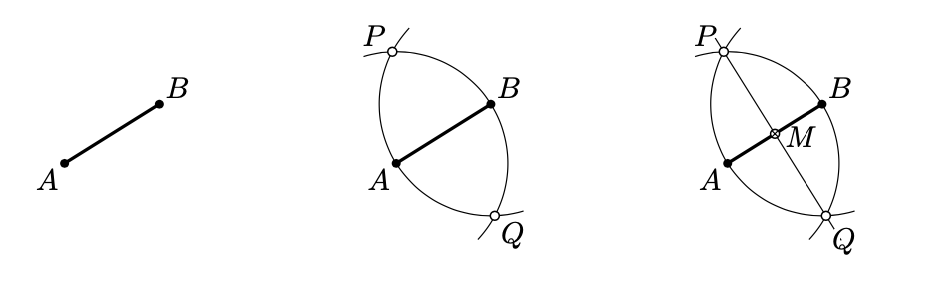
    2021-02-08 пнг

    Як правило, потрібно довести, що конструкція виробляє те, що очікувалося. Ось доказ для наведеного вище прикладу.

    Доказ

    Відповідно до теореми 5.2.1,\((PQ)\) це перпендикулярна бісектриса до\([AB]\). Таким чином,\(M = (AB) \cap (PQ)\) є серединою\([AB]\).

    Вправа\(\PageIndex{1}\)

    Зробіть лінійку і компас побудови лінії через задану точку, яка перпендикулярна до даної лінії.

    Підказка

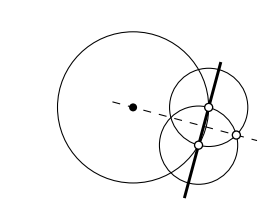
    2021-02-08 пн

    Вправа\(\PageIndex{2}\)

    Зробіть лінійку і циркуль побудови центру заданого кола.

    Підказка

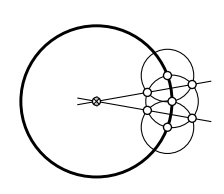
    2021-02-08 пл.

    Вправа\(\PageIndex{1}\)

    Зробіть лінійку і компас побудова ліній tan- gent до заданого кола, які проходять через задану точку.

    Підказка

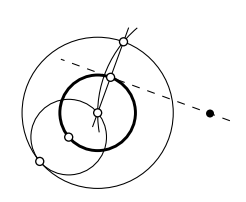
    2021-02-08 пл.

    Вправа\(\PageIndex{1}\)

    Дано два кола\(\Gamma_1\) і\(\Gamma_2\) і відрізок\([AB]\) зробити лінійку і циркуль побудова кола з радіусом\(AB\), який дотичний до кожного кола\(\Gamma_1\) і\(\Gamma_2\).

    Підказка

    2021-02-08 пл.