38.2: Побудова координатної площини

Урок

Розберемо різні способи створення координатної площини.

Вправа$\PageIndex{1}$: English Writer

Наступні дані були зібрані протягом одного грудневого дня в Англії.

Таблиця$\PageIndex{1}$

час після полудня (годин)	температура ($^{\circ}\text{C}$)
$0$	\ (^ {\ circ}\ текст {C}\)) ">$5$
$1$	\ (^ {\ circ}\ текст {C}\)) ">$3$
$2$	\ (^ {\ circ}\ текст {C}\)) ">$4$
$3$	\ (^ {\ circ}\ текст {C}\)) ">$2$
$4$	\ (^ {\ circ}\ текст {C}\)) ">$1$
$5$	\ (^ {\ circ}\ текст {C}\)) ">$-2$
$6$	\ (^ {\ circ}\ текст {C}\)) ">$-3$
$7$	\ (^ {\ circ}\ текст {C}\)) ">$-4$
$8$	\ (^ {\ circ}\ текст {C}\)) ">$-4$

Малюнок$\PageIndex{1}$

Малюнок$\PageIndex{2}$

Малюнок$\PageIndex{3}$

1. Який набір осей ви б обрали для представлення цих даних? Поясніть свої міркування.
2. Поясніть, чому інші два набори осей не здавалися такими доречними, як той, який ви вибрали.

Вправа$\PageIndex{2}$: Axes Drawing Decisions

1. Ось три набори координат. Для кожного набору намалюйте і позначте відповідну пару осей і намалюйте точки.

1. $(1,2), (3,-4), (-5,-2), (0, 2.5)$

Малюнок$\PageIndex{4}$

2. $(50,50), (0,0), (-10, -30), (-35,40)$

Малюнок$\PageIndex{5}$

3. $\left(\frac{1}{4},\frac{3}{4}\right), \left(\frac{-5}{4},\frac{1}{2}\right), \left(-1\frac{1}{4},\frac{-3}{4}\right), \left(\frac{1}{4},\frac{-1}{2}\right)$

Малюнок$\PageIndex{6}$

2. Обговоріть з партнером:

• Чим відрізняються осі та мітки ваших трьох креслень?
• Як координати вплинули на те, як ви намалювали осі та позначали цифри?

Вправа$\PageIndex{3}$: Positively A-maze-ing

Ось лабіринт на координатній площині. Чорна точка в центрі - (0, 0). Сторона кожного квадрата сітки становить 2 одиниці довжини.

1. Входимо в вищезгаданий лабіринт в локації, позначеної зеленим відрізком. Намалюйте відрізки лінії, щоб показати свій шлях через і з лабіринту. Позначте кожну точку повороту буквою. Потім перерахуйте всі літери і напишіть їх координати.
2. Виберіть будь-які 2 поворотні точки, які поділяють один і той же відрізок лінії. Що ж стосується їх координат? Поясніть, чому вони поділяють цю функцію.

Ви готові до більшого?

Щоб дістатися від точки$(2,1)$ до$(-4,3)$ можна пройти дві одиниці вгору і шість одиниць вліво, на загальну відстань вісім одиниць. Це називається «відстань таксі», тому що таксист повинен був проїхати вісім блоків, щоб потрапити між цими двома точками на карті.

Малюнок$\PageIndex{7}$

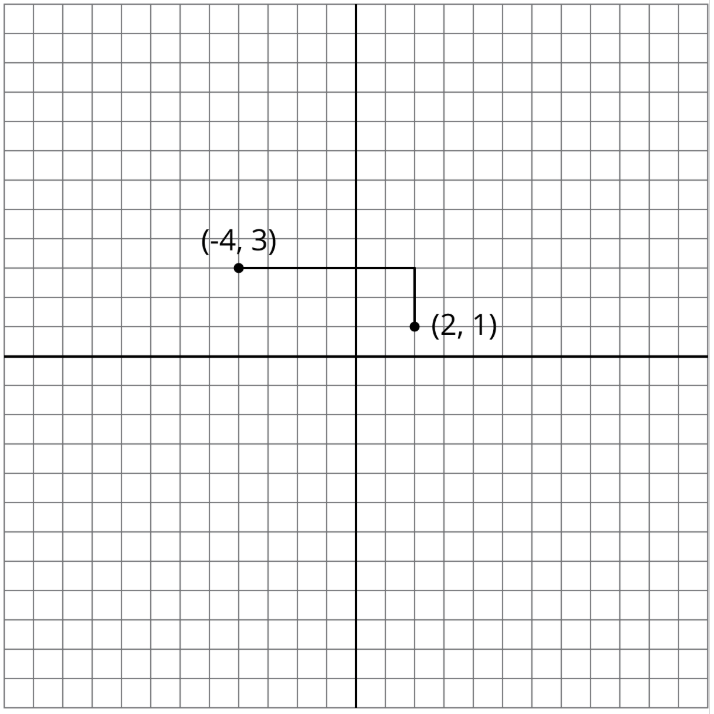
Знайти якомога більше очок, як ви можете, що таксі відстань вісім одиниць від$(2,1)$. Яку форму складають ці точки?

Резюме

Координатна площина може бути використана для відображення інформації за участю пар чисел.

Використовуючи координатну площину, ми повинні звернути пильну увагу на те, що представляє кожна вісь і який масштаб використовує кожна.

Припустимо, ми хочемо скласти наступні дані про температуру в Міннеаполісі одного вечора.

Таблиця$\PageIndex{2}$

час (годин з півночі)	температура (градуси С)
$-4$	$3$
$-1$	$-2$
$0$	$-4$
$3$	$-8$

Ми можемо вирішити, що$x$ -вісь представляє кількість годин по відношенню до півночі, а$y$ вісь -представляє температуру в градусах Цельсія.

• У цьому випадку$x$ -значення менше 0 представляють години до півночі, а$x$ -значення більше 0 представляють години після півночі.
• На$y$ осі -значення представляють температуру вище і нижче точки замерзання 0 градусів Цельсія.

Дані включають цілі числа, тому доречно, щоб кожен квадрат на сітці представляв собою ціле число.

• Зліва від початку,$x$ -вісь повинна пройти аж до -4 або менше (далі вліво). Праворуч йому потрібно перейти на 3 або більше.
• Нижче походження,$y$ -вісь повинна йти аж до -8 або нижче. Над початком її потрібно перейти на 3 або вище.

Ось графік даних з осями, позначені відповідним чином.

Малюнок$\PageIndex{8}$: Координатна площина, початок O, горизонтальна вісь, час у годинами після півночі, негативні від 8 до 10 одиниць, вертикальна вісь, температура в градусах Цельсія, негативні від 8 до 6 одиниць. Точки на (негативний 4 кома 30), (негативний 1 кома 2), (нульова кома негативний 4), (3 кома негативний 8).

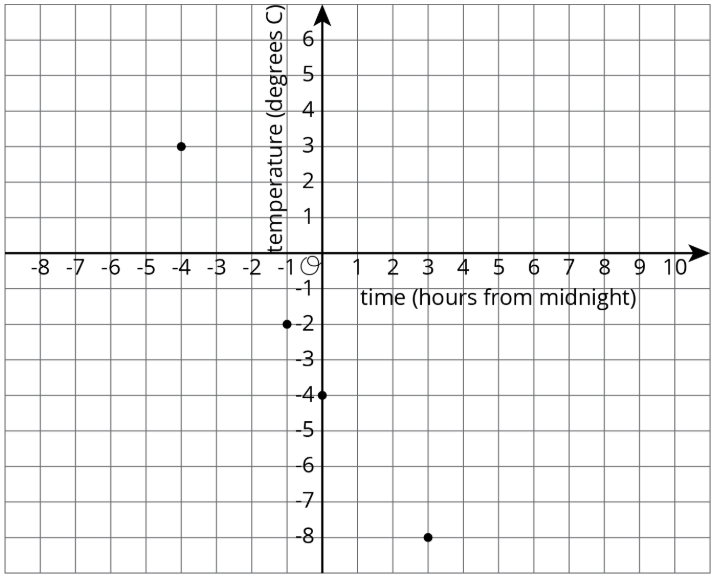
На цій координатній площині точка в$(0,0)$ означатиме температуру 0 градусів Цельсія опівночі. Точка в$(-4,3)$ означає температуру 3 градуси Цельсія за 4 години до півночі (або 20:00).

Записи глосарію

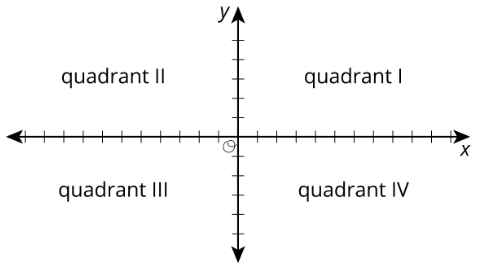
Визначення: Квадрант

Координатна площина розділена на 4 області, які називаються квадрантами. Квадранти нумеруються римськими цифрами, починаючи з правого верхнього кута.

Малюнок$\PageIndex{9}$

Практика

Вправа$\PageIndex{4}$

Намалюйте та позначте відповідну пару осей і намалюйте точки.

$\left(\frac{1}{5},\frac{4}{5}\right)$

$\left(-\frac{3}{5},\frac{2}{5}\right)$

$\left(-1\frac{1}{5},-\frac{4}{5}\right)$

$\left(\frac{1}{5},-\frac{3}{5}\right)$

Вправа$\PageIndex{5}$

Дієго попросили намітити такі моменти:$(-50,0), (150,100), (200,-100), (350, 50), (-250, 0)$. Який інтервал він міг би використовувати для кожної осі? Поясніть свої міркування.

Вправа$\PageIndex{6}$

1. Назвіть 4 точки, які утворювали б квадрат з початком у його центрі.
2. Графік цих точок, щоб перевірити, чи утворюють вони квадрат.

Вправа$\PageIndex{7}$

Яку з наведених нижче змін ви б представили за допомогою від'ємного числа? Поясніть, що позитивне число буде представляти в цій ситуації.

1. Втрата 4 бали
2. Приріст 50 ярдів
3. Втрата $10
4. Висота над рівнем моря

(Від блоку 7.1.5)

Вправа$\PageIndex{8}$

Джада купує зошити для школи. Вартість кожного блокнота становить $1,75.

1. Напишіть рівняння, яке показує вартість зошитів Джади$c$, з точки зору кількості зошитів$n$, які вона купує.
2. Які з наступного можуть бути точками на графіку вашого рівняння?

$(1.75, 1)\qquad (2, 3.50)\qquad (5,8.75)\qquad (17.50,10)\qquad (9, 15.35)$

(З блоку 6.4.1)

Вправа$\PageIndex{9}$

Кукурудзяне поле має площу 28,6 акрів. Для цього потрібно близько 15 000 000 галонів води. Про те, скільки галонів води на акр це?

1. $5,000$
2. $50,000$
3. $500,000$
4. $5,000,000$

(Від блоку 5.4.5)