Skip to main content
LibreTexts - Ukrayinska

38.1: Точки на координатній площині

  1. Last updated
  2. Save as PDF
  • Page ID
    893

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте досліджуємо і продовжимо координатну площину.

    Вправа\(\PageIndex{1}\): Guess My Line

    1. Виберіть горизонтальну або вертикальну лінію на сітці. Намалюйте 4 точки на лінії і позначте кожну точку своїми координатами.
    clipboard_e14b12daa515cee51cda291bece120a23.png
    Малюнок\(\PageIndex{1}\)
    1. Повідомте своєму партнеру, чи є ваша лінія горизонтальною або вертикальною, і пустіть партнера вгадати розташування ваших точок, назвавши координати.
      Якщо припущення вірне, поставте X через точку. Якщо ваш партнер вгадав точку, яка знаходиться на вашій лінії, але не ту точку, яку ви намалювали, скажіть: «Ця точка знаходиться на моїй лінії, але не є однією з моїх точок».
      По черзі вгадуючи один одному точки, по 3 здогадки за хід.

    Вправа\(\PageIndex{2}\): The Coordinate Plane

    clipboard_e5c7e22ee8b97942316c17d36564f8270.png
    Малюнок\(\PageIndex{2}\)

    Кольорові точки на координатній площині схожі на цілі. Натисніть кожну точку, ввівши її координати як впорядковану пару на панелі введення, ось так:

    1. Що ви помічаєте про локаціях і впорядкованих парах\(B, C,\) і\(D\)? Чим вони відрізняються від таких для точки\(A\)?
    2. Ділянка точки в\((-2,5)\). Позначте його\(E\). Ділянка ще однієї точки на\((3,-4.5)\). Позначте його\(F\).
    3. Координатна площина розділена на чотири квадранти, I, II, III та IV, як показано тут.
    clipboard_e83ed440b6d4e2eef06c2f224a002ed5b.png
    Малюнок\(\PageIndex{3}\)
    • \(G=(5,2)\)
    • \(H=(-1, -5)\)
    • \(I=(7,-4)\)
    1. В якому квадранті\(G\) знаходиться? \(H\)? \(I\)?
    2. Точка має позитивну\(y\) -координату. В якому квадранті це може бути?

    Вправа\(\PageIndex{3}\): Coordinated Archery

    Ось зображення мішені для стрільби з лука на координатній площині. Оцінки за посадку стрілки в кольорових областях такі:

    • Жовтий: 10 балів
    • Червоний: 8 балів
    • Синій: 6 балів
    • Зелений: 4 бали
    • Білий: 2 бали

    Назвіть координати можливої точки посадки, яку потрібно забити:

    1. 6 балів
    2. 10 балів
    3. 2 бали
    4. Немає очок
    5. 4 бали
    6. 8 балів
    clipboard_e6f3689061467160a4c875e3aacef44c8.png
    Малюнок\(\PageIndex{4}\)

    Введіть координати для кожної точки в окремому рядку, використовуючи дужки. Ось так:

    Ви готові до більшого?

    Уявіть, що ви застрягли в координатній площині. Ви можете робити лише вертикальні та горизонтальні кроки довжиною в одну одиницю.

    1. Скільки способів є, щоб дістатися від точки\((-3,2)\) до,\((-1,-1)\) якщо ви будете тільки крок вниз і вправо?
    2. Скільки способів є, щоб дістатися від точки\((-1,-2)\) до,\((4,0)\) якщо ви можете тільки крок вгору і вправо?
    3. Складіть ще деякі проблеми, подібні до цього, і подивіться, які закономірності ви помітили.

    Резюме

    Так само, як числовий рядок може бути розширена вліво, щоб включити негативні числа,\(x\) - і\(y\) -вісь координатної площини також може бути розширена, включивши від'ємні значення.

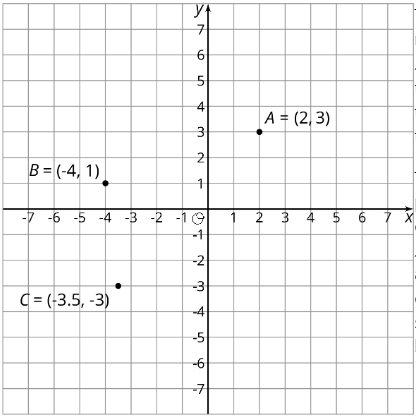
    clipboard_ed588a3fda022ae4198fcd568e15476b9.png
    Малюнок\(\PageIndex{5}\)

    Впорядкована пара\((x,y)\) може мати негативні\(x\) - і\(y\) -значення. Для\(B=(-4,1)\),\(x\) -value -4 говорить нам, що точка 4 одиниці зліва від\(y\) -осі. \(y\)Значення 1 говорить нам, що точка знаходиться на одну одиницю вище\(x\) -осі.

    Це ж міркування стосується\(A\) і пунктів і\(C\). \(x\)- і\(y\) -координати для точки\(A\) є додатними, так\(A\) це праворуч від\(y\) -осі і вище\(x\) -осі. The\(x\) - і\(y\) -координати для точки\(C\) є негативними, так що\(C\) ліворуч від\(y\) -осі і нижче\(x\) -осі.

    Записи глосарію

    Визначення: Квадрант

    Координатна площина розділена на 4 області, які називаються квадрантами. Квадранти нумеруються римськими цифрами, починаючи з правого верхнього кута.

    clipboard_e4b97eb06ad2fd5bca9b70a35616eb423.png
    Малюнок\(\PageIndex{6}\)

    Практика

    Вправа\(\PageIndex{4}\)

    1. Графік цих точок в координатній площині:\((-2,3), (2,3), (-2,-3), (2,-3)\).
    clipboard_ed6af92c1fd2dd8b4085a33849e9ea0eb.png
    Малюнок\(\PageIndex{7}\)
    1. З'єднайте всі точки. Опишіть цифру.

    Вправа\(\PageIndex{5}\)

    Запишіть координати кожної точки.

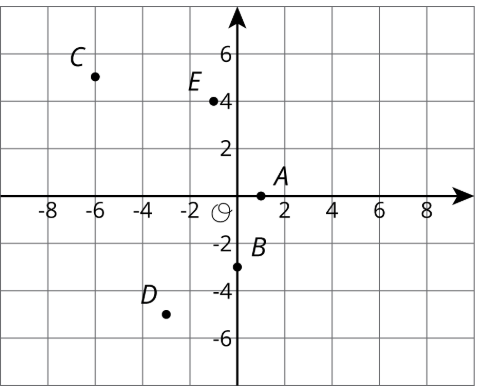
    clipboard_e331f17750dd40ede7c8e45faebf8f08c.png
    Малюнок\(\PageIndex{8}\): Координатна площина, o на початку, горизонтальна вісь -8 до 8 на два, вертикальна вісь негативна від 6 до 6 на два. Точка А на горизонтальній осі, на півдорозі між 0 і 2. Точка B, на вертикальній осі, на півдорозі між негативними 2 і негативними 4. Точка С вище негативної 6 на горизонтальній осі, на півдорозі між 4 і 6. Точка D на півдорозі між негативними 4 та негативними 2 на горизонтальній осі, на півдорозі між негативними 4 та негативними 6 на вертикальній осі. Точка Е між негативними 2 і нулем на горизонтальній осі, поруч з 4 на вертикальній осі.

    Вправа\(\PageIndex{6}\)

    Ці три точки утворюють горизонтальну лінію:\((-3.5, 4), (0,4),\) і\((6.2, 4)\). Назвіть дві додаткові точки, які потрапляють на цю лінію.

    Вправа\(\PageIndex{7}\)

    Одного разу вночі в Тусоні\(24^{\circ}\text{C}\) тепліше, ніж в Міннеаполісі. Якщо температури в Тусоні та Міннеаполісі протилежні, яка температура в Тусоні?

    1. \(-24^{\circ}\text{C}\)
    2. \(-12^{\circ}\text{C}\)
    3. \(12^{\circ}\text{C}\)
    4. \(24^{\circ}\text{C}\)

    (З блоку 7.1.2)

    Вправа\(\PageIndex{8}\)

    Лін пробіг 29 метрів за 10 секунд. Вона бігала з постійною швидкістю.

    1. Як далеко Лін пробігав кожну секунду?
    2. При такому темпі, як далеко вона може пробігти за 1 хвилину?

    (Від блоку 2.3.4)

    Вправа\(\PageIndex{9}\)

    Ной допомагає своїй групі продавати коробки шоколаду, щоб фінансувати поїздку на поле. Кожна коробка містить 20 барів, а кожен бар продається за $1.50.

    1. Заповніть таблицю для значень\(m\).
      продані коробки (\(b\)) зібрані гроші (\(m\))
      \ (b\)) ">\(1\) \ (m\)) ">
      \ (b\)) ">\(2\) \ (m\)) ">
      \ (b\)) ">\(3\) \ (m\)) ">
      \ (b\)) ">\(4\) \ (m\)) ">
      \ (b\)) ">\(5\) \ (m\)) ">
      \ (b\)) ">\(6\) \ (m\)) ">
      \ (b\)) ">\(7\) \ (m\)) ">
      \ (b\)) ">\(8\) \ (m\)) ">
      Таблиця\(\PageIndex{1}\)
    2. Напишіть рівняння для суми грошей\(m\), яка буде зібрана, якщо продаються\(b\) коробки шоколадних батончиків. Яка незалежна змінна, а яка є залежною змінною у вашому рівнянні?
    3. Напишіть рівняння для кількості ящиків\(b\), які були продані, якщо були зібрані\(m\) долари. Яка незалежна змінна, а яка є залежною змінною у вашому рівнянні?

    (З блоку 6.4.1)