Skip to main content
LibreTexts - Ukrayinska

38.4: Відстані на координатній площині

  1. Last updated
  2. Save as PDF
  • Page ID
    886

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте вивчимо відстань на координатній площині.

    Вправа\(\PageIndex{1}\): Coordinate Patterns

    Побудуйте точки в призначеному квадранті та позначте їх координатами.

    Вправа\(\PageIndex{2}\): Signs of Numbers in Coordinates

    1. Запишіть координати кожної точки.
    • \(A=\)
    • \(B=\)
    • \(C=\)
    • \(D=\)
    • \(E=\)
    1. Дайте відповідь на ці питання по кожній парі очок.
    • Як координати однакові? Чим вони відрізняються?
    • Як далеко вони знаходяться від осі y? Ліворуч або праворуч від нього?
    • Як далеко вони знаходяться від осі х? Вище чи нижче нього?
    1. \(A\)і\(B\)
    2. \(B\)і\(D\)
    3. \(A\)і\(D\)

    Пауза тут для обговорення класу.

    1. Точка\(F\) має ті ж координати, що і точка\(C\), за винятком того, що її\(y\) -координата має протилежний знак.
    1. Покладіть точку\(F\) на координатній площині і позначте її координатами.
    2. Як далеко знаходяться\(F\) і\(C\) від\(x\) -осі?
    3. Яка відстань між\(F\) і\(C\)?
    1. Точка\(G\) має ті ж координати, що і точка\(E\), за винятком того, що її\(x\) -координата має протилежний знак.
      1. Покладіть точку\(G\) на координатній площині і позначте її координатами.
      2. Як далеко знаходяться\(G\) і\(E\) від\(y\) -осі?
      3. Яка відстань між і?
    2. Точка\(H\) має ті ж координати, що і точка\(B\), за винятком того, що обидві її координати мають протилежні знаки. В якому квадранті знаходиться точка\(H\)?

    Вправа\(\PageIndex{3}\): Finding Distances on a Coordinate Plane

    1. Позначте кожну точку своїми координатами.
    2. Знайдіть відстань між кожною з наступних пар точок.
      1. Точка\(B\) і\(C\)
      2. Точка\(D\) і\(B\)
      3. Точка\(D\) і\(E\)
    3. З яких пунктів 5 одиниць\((-1.5,-3)\)?
    4. Які з пунктів складають 2 одиниці з\((0.5,-4.5)\)?
    5. Побудувати точку, яка є як 2.5 одиниць від\(A\) і 9 одиниць від\(E\). Позначте цю точку\(F\) та запишіть її координати.

    Ви готові до більшого?

    Прия каже: «Є рівно чотири точки, від яких 3 одиниці»\((-5,0)\). Лін каже: «Я думаю, що є ціла купа точок, які знаходяться на відстані 3 одиниць»\((-5,0)\).

    Чи згодні ви з будь-яким з них? Поясніть свої міркування.

    Резюме

    Точки\(A=(5,2), B=(-5,2), C=(-5,-2),\) і\(D=(5,-2)\) відображаються в площині. Зверніть увагу, що всі вони мають майже однакові координати, за винятком того, що знаки різні. Всі вони знаходяться на однаковій відстані від кожної осі, але знаходяться в різних квадрантах.

    clipboard_ee3708c4feec23f3bee0122fe14a83932.png
    Малюнок\(\PageIndex{1}\)

    Зверніть увагу, що вертикальна відстань між точками\(A\) і\(D\) становить 4 одиниці, тому що точка\(A\) знаходиться на 2 одиниці вище горизонтальної осі, а точка\(D\) на 2 одиниці нижче горизонтальної осі. Горизонтальна відстань між точками\(A\) і\(B\) становить 10 одиниць, тому що точка\(B\) знаходиться на 5 одиниць зліва від вертикальної осі і точка\(A\) 5 одиниць праворуч від вертикальної осі.

    Ми завжди можемо визначити, в якому квадранті знаходиться точка за знаками її координат.

    \(x\) \(y\) квадрант
    \ (x\) ">позитивний \ (y\) ">позитивний Я
    \ (x\) ">негативний \ (y\) ">позитивний II
    \ (x\) ">негативний \ (y\) ">негативний III
    \ (x\) ">позитивний \ (y\) ">негативний IV
    Таблиця\(\PageIndex{1}\)
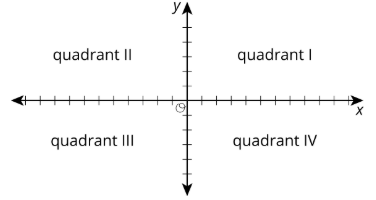
    clipboard_eae552a82357273a795d0c57f85e1433d.png
    Малюнок\(\PageIndex{2}\)

    Загалом:

    • Якщо дві точки мають\(x\) -координати, які є протилежними (наприклад, 5 і -5), вони знаходяться на однаковій відстані від вертикальної осі, але одна - ліворуч, а інша праворуч.
    • Якщо дві точки мають\(y\) -координати, які є протилежними (наприклад, 2 та -2), вони знаходяться на однаковій відстані від горизонтальної осі, але одна знаходиться вище, а інша внизу.

    Коли дві точки мають однакове значення для першої або другої координати, ми можемо знайти відстань між ними, віднімаючи різні координати. Для прикладу розглянемо\((1,3)\) і\((5,3)\):

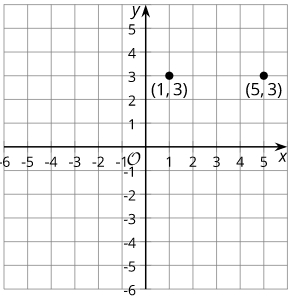
    clipboard_ec17fcfeb25e2e39554965c3ede65a356.png
    Малюнок\(\PageIndex{3}\)

    Вони мають однакову\(y\) -координату. Якщо відняти\(x\) -координати, ми отримаємо\(5-1=4\). Ці точки знаходяться на 4 одиниці один від одного.

    Записи глосарію

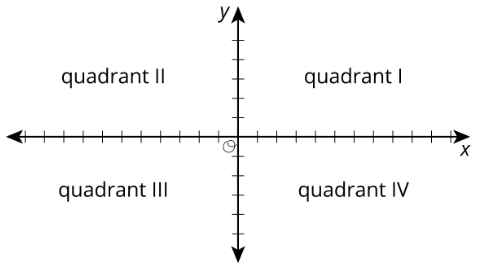
    Визначення: Квадрант

    Координатна площина розділена на 4 області, які називаються квадрантами. Квадранти нумеруються римськими цифрами, починаючи з правого верхнього кута.

    clipboard_e4b97eb06ad2fd5bca9b70a35616eb423.png
    Малюнок\(\PageIndex{4}\)

    Практика

    Вправа\(\PageIndex{4}\)

    Ось 4 точки на координатній площині.

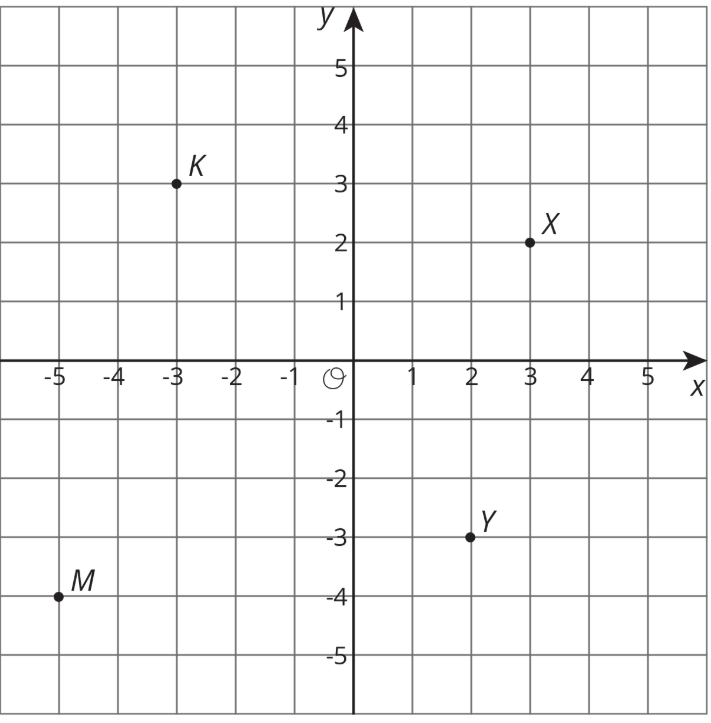
    clipboard_e23aafa34b3602e2c957126a584a243e6.png
    Малюнок\(\PageIndex{5}\)
    1. Позначте кожну точку своїми координатами.
    2. Побудуйте точку, яка знаходиться в 3 одиницях від точки\(K\). Позначте його\(P\).
    3. Побудувати точку, яка знаходиться в 2 одиниць від точки\(M\). Позначте його\(W\).

    Вправа\(\PageIndex{5}\)

    Кожна множина точок з'єднується, утворюючи відрізок лінії. Яка довжина кожного?

    1. \(A=(3,5)\)і\(B=(3,6)\)
    2. \(C=(-2,-3)\)і\(D=(-2,-6)\)
    3. \(E=(-3,1)\)і\(F=(-3,-1)\)

    Вправа\(\PageIndex{6}\)

    На координатній площині намалюйте чотири точки, які знаходяться на відстані 3 одиниць від точки\(P=(-2,-1)\). Запишіть координати кожної точки.

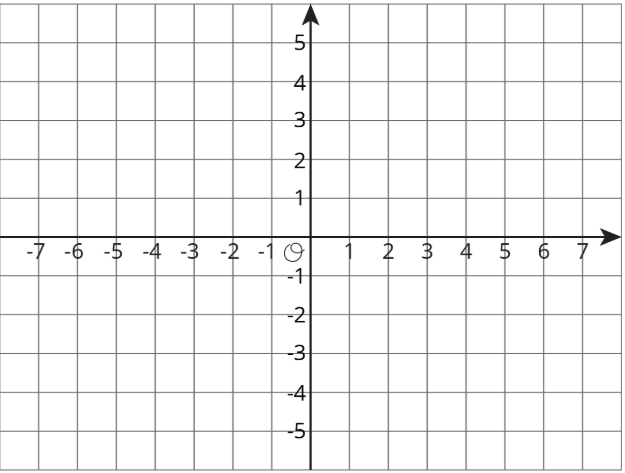
    clipboard_e5afb40555ec7cf0479e824cc98ce1038.png
    Малюнок\(\PageIndex{6}\)

    Вправа\(\PageIndex{7}\)

    Рецепт Ноя для ігристого апельсинового соку використовує 4 літри апельсинового соку і 5 літрів газованої води.

    1. Ной готує великі партії ігристого апельсинового соку для шкільних вечірок. Він зазвичай знає загальну кількість літрів\(t\), що йому потрібно приготувати. Напишіть рівняння, яке показує\(s\), як Ной може знайти, кількість літрів газованої води, якщо він знає\(t\).
    2. Іноді школа купує певну кількість\(j\), літрів апельсинового соку і Ною потрібно з'ясувати, скільки ігристого апельсинового соку він може зробити. Напишіть рівняння, яке Ной може використовувати, щоб знайти,\(t\) якщо він знає\(j\).

    (З блоку 6.4.1)

    Вправа\(\PageIndex{8}\)

    Щоб валізу перевіряли на рейсі (замість того, щоб носити вручну), він може важити не більше 50 фунтів. Валіза Андре важить 23 кілограми. Чи може Андре перевірити свою валізу? Поясніть або покажіть свої міркування. (Примітка: 10 кілограмів\(\approx\) 22 фунтів)

    (Від блоку 3.2.3)