22.3: Використання діаграм для пошуку кількості груп

Last updated
Save as PDF

Page ID: 910

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Урок

Давайте намалюємо стрічкові діаграми, щоб подумати про поділ на дроби.

Вправа\(\PageIndex{1}\): How Many of These in That?

Ми можемо думати про вираз поділу\(10\div 2\frac{1}{2}\) як питання: «Скільки груп\(2\frac{1}{2}\) в 10?» Завершіть стрічкову схему, щоб представити це питання. Тоді знайдіть відповідь.

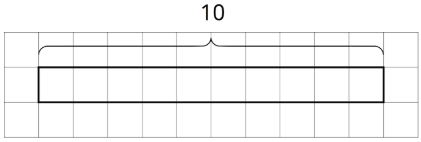
Заповніть стрічкову схему, щоб представити питання: «Скільки груп по 2 в 7?» Тоді знайдіть відповідь.

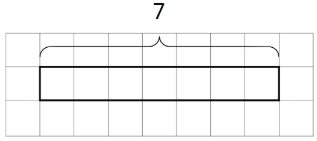
Вправа\(\PageIndex{2}\): Representing Groups of Fractions with Tape Diagrams

Щоб зрозуміти питання «Скільки\(\frac{2}{3}\) s в 1? ,» Андре написав рівняння і намалював стрічкову діаграму.

\(?\cdot\frac{2}{3}=1\)

\(1\div\frac{2}{3}=?\)

Малюнок\(\PageIndex{3}\): Стрічкова схема з трьома рівними частинами. Перші дві частини затінені і кожна з них позначені одна третина, всього 1. Кронштейн маркується 1 групою з двох третин, і містить перші дві частини.

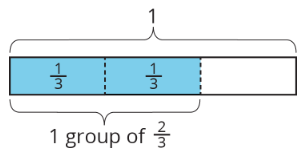
У попередньому завданні ми використовували блоки шаблонів, щоб допомогти нам вирішити рівняння\(1\div\frac{2}{3}=?\). Поясніть, як стрічкова діаграма Андре також може допомогти нам вирішити рівняння.
Напишіть рівняння множення та рівняння ділення для кожного питання. Потім намалюйте стрічкову схему і знайдіть відповідь.

Скільки\(\frac{3}{4}\) s знаходяться в\(1\)?

Скільки\(\frac{2}{3}\) s знаходяться в\(3\)?

Скільки\(\frac{3}{2}\) s знаходяться в\(5\)?

Вправа\(\PageIndex{3}\): Finding Number of Groups

Напишіть рівняння множення або рівняння ділення для кожного питання. Потім знайдіть відповідь і поясніть або покажіть свої міркування.
1. Скільки книг товщиною\(\frac{3}{8}\) дюймів роблять стек, який має висоту 6 дюймів?
2. Скільки груп\(\frac{1}{2}\) фунтів в\(2\frac{3}{4}\) фунтах?
Напишіть питання, яке можна представити рівнянням ділення\(5\div 1\frac{1}{2}=?\). Потім знайдіть відповідь і поясніть або покажіть свої міркування.

Резюме

Пекар використовував 2 кілограми борошна, щоб зробити кілька партій рецептури тіста. У рецептурі\(\frac{2}{5}\) вказано кілограм борошна на заміс. Скільки партій вона зробила?

Можна придумати питання так: «Скільки груп\(\frac{2}{5}\) кілограм складають 2 кілограми?» і представляють це питання за допомогою рівнянь:

\(?\cdot\frac{2}{5}=2\)

\(2\div\frac{2}{5}=?\)

Щоб допомогти нам розібратися в питанні, ми можемо намалювати стрічкову схему. На цій схемі зображено 2 цілих кілограма, причому кожен кілограм розділений на п'яті.

Малюнок\(\PageIndex{7}\): Лінійна діаграма дробів. 10 рівних частин. Кожна частина маркується фракцією 1 над 5. Всього маркуються 2 кілограми і партії знаків питання. Кожні дві частини маркуються 1 партією.

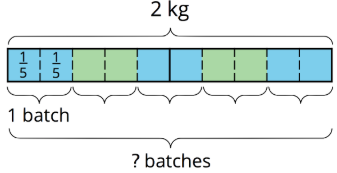
Ми бачимо, що є 5 груп\(\frac{2}{5}\) у 2. Множення 5 і\(\frac{2}{5}\) дозволяє нам перевірити цю відповідь:\(5\cdot\frac{2}{5}=\frac{10}{5}\) і\(\frac{10}{5}=2\), так відповідь правильна.

Зверніть увагу, що кількість груп, які\(2\div\frac{2}{5}\) є результатом є ціле число. Іноді кількість груп, які ми знаходимо від ділення, може бути не цілим числом. Ось приклад:

Припустимо, одна порція рису - це\(\frac{3}{4}\) чашка. Скільки порцій в\(3\frac{1}{2}\) чашках?

\(?\cdot\frac{3}{4}=3\frac{1}{2}\)

\(3\frac{1}{2}\div\frac{3}{4}=?\)

Малюнок\(\PageIndex{8}\): Лінійна діаграма дробів. 16 рівних частин. 14 частин заштриховані. 14 частин позначені невідомою кількістю груп і 3 з половиною чашки. Кожна частина маркується фракцією 1 над 4. Спочатку 3 частини маркуються 1 порцією.

Дивлячись на діаграму, ми можемо побачити, що є 4 повні групи\(\frac{3}{4}\), плюс 2 четвертих. Якщо 3 четверті складають цілу групу, то 2 четверті\(\frac{2}{3}\) складають групу. Отже, кількість порцій («?» в кожному рівнянні) є\(4\frac{2}{3}\). Ми можемо перевірити це, множивши\(4\frac{2}{3}\) і\(\frac{3}{4}\).

\(4\frac{2}{3}\cdot\frac{3}{4}=\frac{14}{3}\cdot\frac{3}{4}\), і\(\frac{14}{3}\cdot\frac{3}{4}=\frac{14}{4}\), що дійсно еквівалентно\(3\frac{1}{2}\).

Практика

Вправа\(\PageIndex{4}\)

Ми можемо думати про\(3\div\frac{1}{4}\) питання «Скільки груп\(\frac{1}{4}\) в\(3\)?» Намалюйте стрічкову схему, щоб представити це питання. Тоді знайдіть відповідь.

Вправа\(\PageIndex{5}\)

Опишіть, як намалювати стрічкову схему, щоб зобразити і відповісти\(3\div\frac{3}{5}=?\) для одного, який був відсутній.

Вправа\(\PageIndex{6}\)

Скільки груп\(\frac{1}{2}\) дня за 1 тиждень?

Напишіть рівняння множення або рівняння ділення, щоб представити питання.
Намалюйте стрічкову діаграму, щоб показати взаємозв'язок між величинами і відповісти на питання. При необхідності використовуйте графічний папір.

Вправа\(\PageIndex{7}\)

Дієго сказав, що відповідь на питання «Скільки груп\(\frac{5}{6}\) знаходяться в\(1\)?» є\(\frac{6}{5}\) або\(1\frac{1}{5}\). Чи згодні ви з ним? Поясніть або покажіть свої міркування.

Вправа\(\PageIndex{8}\)

Виберіть всі рівняння, які можуть представляти питання: «Скільки груп\(\frac{4}{5}\) знаходяться в\(1\)?»

\(?\cdot 1=\frac{4}{5}\)
\(1\cdot\frac{4}{5}=?\)
\(\frac{4}{5}\div 1=?\)
\(?\cdot\frac{4}{5}=1\)
\(1\div\frac{4}{5}=?\)

(З блоку 4.2.2)

Вправа\(\PageIndex{9}\)

Розрахуйте кожен відсоток подумки.

Що\(10\) таке% від\(70\)?
Що\(10\) таке% від\(110\)?
Що\(25\) таке% від\(160\)?
Що\(25\) таке% від\(48\)?
Що\(50\) таке% від\(90\)?
Що\(50\) таке% від\(350\)?
Що\(75\) таке% від\(300\)?
Що\(75\) таке% від\(48\)?

(Від блоку 3.4.5)