12.2: Критерій стабільності Найквіста
- Page ID
- 62708
Критерій Найквіста - це графічна техніка для визначення того, чи можна стабілізувати нестабільну лінійну інваріантну систему часу за допомогою петлі негативного зворотного зв'язку. Ми трохи уважніше розглянемо такі системи, коли вивчимо перетворення Лапласа в наступній темі. Для цієї теми ми задовольнимося постановкою проблеми лише з найменшим фізичним контекстом.
Ви вже стикалися з лінійними інваріантними системами часу в 18.03 (або його еквіваленті), коли ви вирішували лінійні диференціальні рівняння з постійним коефіцієнтом.
Системні функції
Лінійна інваріантна система часу має системну функцію, яка є функцією комплексної змінної. Зазвичай комплексна змінна позначається\(s\) і для системної функції використовується велика літера.
Нехай\(G(s)\) буде така системна функція. Зробимо стандартне припущення, яке\(G(s)\) є мероморфним з скінченною кількістю (скінченних) полюсів. Це припущення тримається в багатьох цікавих випадках. Наприклад, досить часто\(G(s)\) є раціональною функцією\(Q(s)/P(s)\) (\(Q\)і\(P\) є поліномами).
Нас буде турбувати стабільність роботи системи.
Система з системною функцією\(G(s)\) називається стабільною, якщо всі полюси\(G\) знаходяться в лівій півплощині. Тобто, якщо всі полюси\(G\) мають негативну реальну частину.
Система називається нестійкою, якщо будь-які полюси знаходяться в правій півплощині, тобто мають позитивну дійсну частину.
Для крайнього випадку, коли жоден полюс не має позитивної реальної частини, але деякі чисто уявні ми будемо називати систему незначно стабільною. Цей випадок можна проаналізувати за допомогою наших методик. Для наших цілей буде потрібно і контур з відступом уздовж уявної осі. Якщо у нас буде час, ми зробимо аналіз.
Чи\(G(s) = \dfrac{s}{(s + 2) (s^2 + 4s + 5)}\) стабільна система з системною функцією?
Рішення
Полюси є\(-2, -2\pm i\). Так як всі вони знаходяться в лівій півплощині, система стабільна.
Чи\(G(s) = \dfrac{s}{(s^2 - 4) (s^2 + 4s + 5)}\) стабільна система з системною функцією?
Рішення
Полюси є\(\pm 2, -2 \pm i\). Так як один полюс знаходиться в правій півплощині, система нестабільна.
Чи\(G(s) = \dfrac{s}{(s + 2) (s^2 + 4)}\) стабільна система з системною функцією?
Рішення
Полюси є\(-2, \pm 2i\). У правій півплощині немає полюсів. Так як на уявній осі є полюси, система незначно стійка.
Термінологія. Поки ми були обережні, щоб сказати «система з системною функцією\(G(s)\)». Відтепер ми дозволимо собі бути трохи більш випадковими і сказати «систему\(G(s)\)». Вона абсолютно ясна і скочується з мови трохи легше!
Діаграми полюс-нуль
Ми можемо візуалізувати\(G(s)\) за допомогою діаграми полюс-нуль. Це діаграма в\(s\) -площині, де ми ставимо невеликий хрест на кожному полюсі і мале коло на кожному нулі.
Дайте діаграми нульових полюсів для кожної з систем
\[G_1(s) = \dfrac{s}{(s + 2) (s^2 + 4s + 5)}, \ \ \ G_1(s) = \dfrac{s}{(s^2 - 4) (s^2 + 4s + 5)}, \ \ \ G_1(s) = \dfrac{s}{(s + 2) (s^2 + 4)}\]
Рішення
Це ті ж системи, що і в прикладах трохи вище. Спочатку відзначимо, що всі вони мають єдиний нуль у початку. Таким чином, ми ставимо коло біля початку і хрест на кожному полюсі.
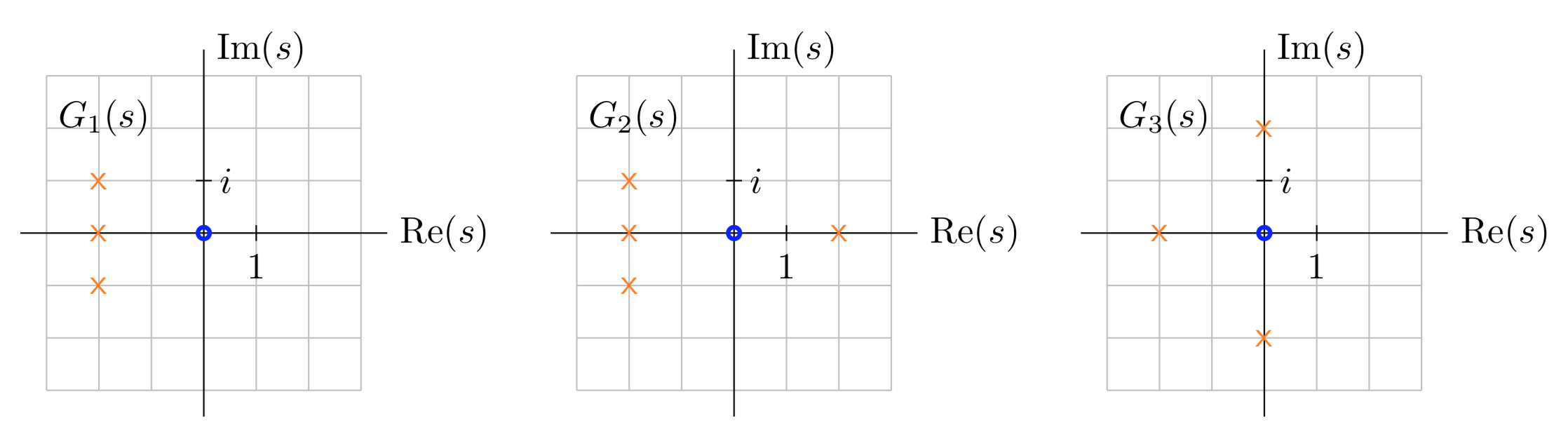
Діаграми полюс-нуль для трьох систем.
трохи про стабільність
Це просто для того, щоб дати вам трохи фізичної орієнтації. З огляду на наше визначення стійкості вище, ми могли б, в принципі, обговорювати стабільність без найменшого уявлення про те, що вона означає для фізичних систем.
Полюси\(G(s)\) відповідають тому, що називаються режимами роботи системи. Простий полюс при\(s_1\) відповідає режиму\(y_1 (t) = e^{s_1 t}\). Система стабільна, якщо всі режими затухають до 0, тобто якщо полюси знаходяться в лівій півплощині.
Фізично режими говорять нам про поведінку системи, коли вхідний сигнал дорівнює 0, але є початкові умови. Полюс з позитивною реальною частиною відповідав би режиму, який переходить до нескінченності у\(t\) міру зростання. Безумовно, розумно назвати систему, яка робить це у відповідь на нульовий сигнал (часто називають «без входу») нестабільною.
Щоб зв'язати це з 18.03: якщо система моделюється диференціальним рівнянням, режими відповідають однорідним розв'язкам\(y(t) = e^{st}\), де\(s\) є корінь характеристичного рівняння. У 18.03 ми назвали систему стабільною, якщо кожен однорідний розчин розпадається до 0. Тобто, якщо непримусова система завжди влаштовувалася до рівноваги.
Системи замкнутого циклу
Якщо система з системною функцією\(G(s)\) нестабільна, її іноді можна стабілізувати за допомогою так званого петлі негативного зворотного зв'язку. Нова система називається замкнутою системою. Його системна функція задається формулою Блек
\[G_{CL} (s) = \dfrac{G(s)}{1 + kG(s)},\]
де\(k\) називається коефіцієнтом зворотного зв'язку. Ми просто приймемо цю формулу. Будь-який клас або книга з теорії управління виведе його для вас.
У цьому контексті\(G(s)\) називається системною функцією відкритого циклу.
Оскільки\(G_{CL}\) це системна функція, ми можемо запитати, чи стабільна система.
Полюси функції системи замкнутого контуру,\(G_{CL} (s)\) наведені в Рівнянні 12.3.2, є нулями\(1 + kG(s)\).
- Доказ
-
Дивлячись на Рівняння 12.3.2, є два можливі джерела полюсів для\(G_{CL}\).
- Нулі знаменника\(1 + k G\). Теорема визнає їх.
- Полюси з\(G\). Так як\(G\) є і в чисельнику, і в знаменнику\(G_{CL}\) його повинно бути зрозуміло, що полюси скасовуються. Ми можемо показати це формально, використовуючи серію Laurent. Якщо\(G\) має полюс порядку\(n\) в\(s_0\) то
\[G(s) = \dfrac{1}{(s - s_0)^n} (b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + a_1 (s - s_0)^{n + 1} + \ ...),\]
де\(b_n \ne 0\). Отже,
\[\begin{array} {rcl} {G_{CL} (s)} & = & {\dfrac{\dfrac{1}{(s - s_0)^n} (b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + \ ...)}{1 + \dfrac{k}{(s - s_0)^n} (b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + \ ...)}} \\ { } & = & {\dfrac{(b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + \ ...)}{(s - s_0)^n + k (b_n + b_{n - 1} (s - s_0) + \ ... a_0 (s - s_0)^n + \ ...)}} \end{array}\]
який чітко аналітичний в\(s_0\). (У\(s_0\) нього дорівнює\(b_n/(kb_n) = 1/k\).)
Встановіть коефіцієнт зворотного зв'язку\(k = 1\). Припустимо,\(a\) це реально, для яких значень\(a\) є система відкритого циклу\(G(s) = \dfrac{1}{s + a}\) стабільна? При яких значеннях\(a\) відповідна замкнута система\(G_{CL} (s)\) стабільна?
(У цьому прикладі немає особливої причини, яка\(a\) повинна бути реальною. Але у фізичних системах складні полюси, як правило, приходять у сполучених парах.)
Рішення
\(G(s)\)має один полюс в\(s = -a\). Таким чином, він стійкий, коли полюс знаходиться в лівій півплощині, тобто для\(a > 0\).
Функція системи замкнутого циклу
\[G_{CL} (s) = \dfrac{1/(s + a)}{1 + 1/(s + a)} = \dfrac{1}{s + a + 1}.\]
Це має полюс на\(s = -a - 1\), так що він стабільний, якщо\(a > -1\). Контур зворотного зв'язку стабілізував нестабільні системи з розімкнутим контуром\(-1 < a \le 0\). (Власне, для\(a = 0\) розімкнутого контуру незначно стабільний, але він повністю стабілізується замкнутим контуром.)
Алгебра, яка бере участь у скасуванні\(s + a\) терміну в знаменниках, є саме скасуванням, яке робить полюси\(G\) знімних сингулярностей в\(G_{CL}\).
Припустимо\(G(s) = \dfrac{s + 1}{s - 1}\). Чи стабільна система відкритого контуру? Чи стабільна система замкнутого контуру, коли\(k = 2\).
Рішення
\(G(s)\)має полюс у правій півплощині, тому система відкритого контуру не є стабільною. Функція системи замкнутого циклу
\[G_{CL} (s) = \dfrac{G}{1 + kG} = \dfrac{(s + 1)/(s - 1)}{1 + 2(s + 1)/(s - 1)} = \dfrac{s + 1}{3s + 1}.\]
Єдиний полюс знаходиться на\(s = -1/3\), тому система замкнутого контуру стабільна. Це випадок, коли зворотний зв'язок стабілізувала нестабільну систему.
\(G(s) = \dfrac{s - 1}{s + 1}\). Чи стабільна система відкритого контуру? Чи стабільна система замкнутого контуру, коли\(k = 2\).
Рішення
Єдина ділянка\(G(s)\) знаходиться в лівій півплощині, тому система відкритого контуру стабільна. Функція системи замкнутого циклу
\[G_{CL} (s) = \dfrac{G}{1 + kG} = \dfrac{(s - 1)/(s + 1)}{1 + 2(s - 1)/(s + 1)} = \dfrac{s - 1}{3s - 1}.\]
Це має один полюс на\(s = 1/3\), тому система замкнутого контуру нестабільна. Це випадок, коли зворотний зв'язок дестабілізував стабільну систему. Це може статися!
Ділянки Найквіста
Для графіка і критерію Найквіста кривою завжди\(\gamma\) буде уявна\(s\) -вісь. Тобто
\[s = \gamma (\omega) = i \omega, \text{ where } -\infty < \omega < \infty.\]
Для системи\(G(s)\) та\(k\) коефіцієнта зворотного зв'язку графік Найквіста - це графік кривої
\[w = k G \circ \gamma (\omega) = kG(i \omega).\]
Тобто сюжет Найквіста - це зображення уявної осі під картою\(w = kG(s)\).
У\(\gamma (\omega)\) змінній є грецька омега і в\(w = G \circ \gamma\) нас є подвійний u.
Нехай\(G(s) = \dfrac{1}{s + 1}\). Намалюйте сюжет Nyquist с\(k = 1\).
Рішення
У випадку\(G(s)\) є дробовим лінійним перетворенням, тому ми знаємо, що воно відображає уявну вісь на коло. Легко перевірити це коло через початок з центром\(w = 1/2\). Ви також можете перевірити, чи проходить вона за годинниковою стрілкою.
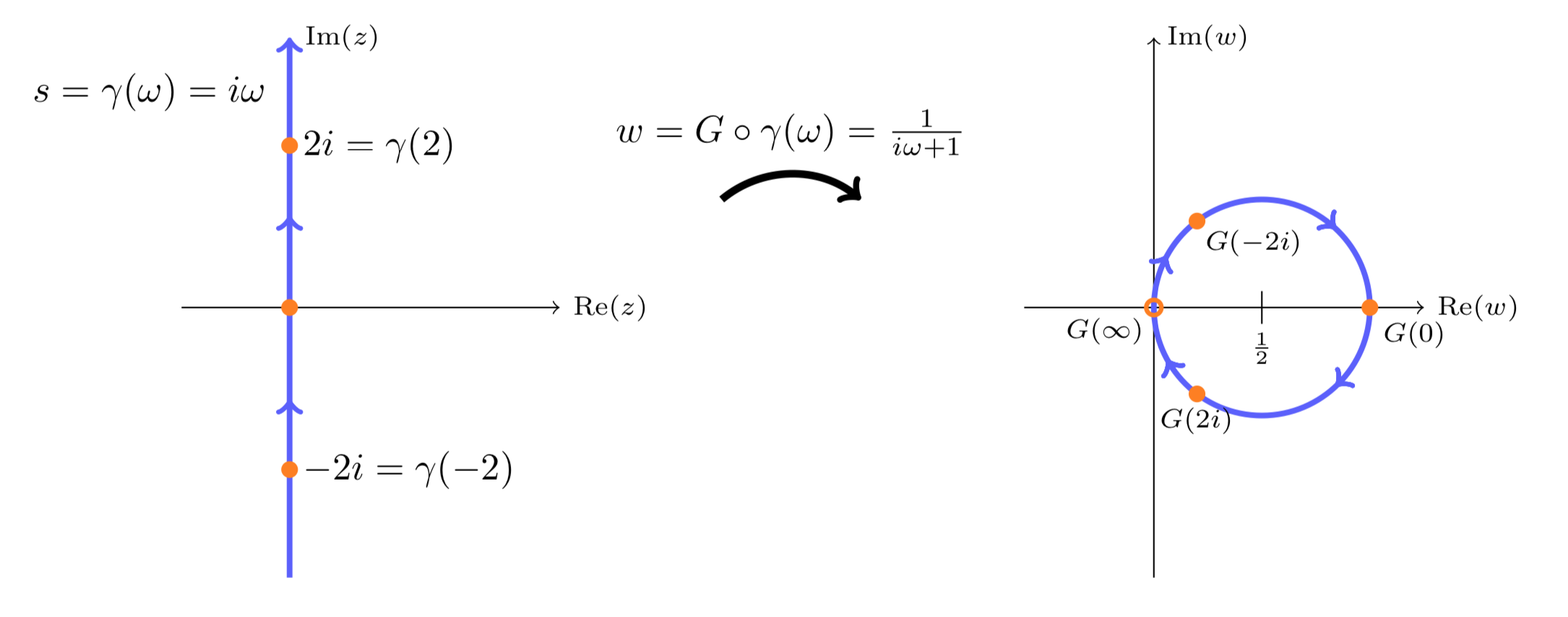
Нюквіст сюжет\(G(s) = 1/(s + 1)\), с\(k = 1\).
Візьмемо\(G(s)\) з попереднього прикладу. Опишіть сюжет Найквіста з коефіцієнтом посилення\(k = 2\).
Рішення
Сюжет Найквіста - це графік\(kG(i \omega)\). \(k = 2\)Коефіцієнт масштабує коло в попередньому прикладі на 2. Тобто сюжет Nyquist - це коло через початок з центром\(w = 1\).
Загалом, коефіцієнт зворотного зв'язку буде якраз масштабувати сюжет Nyquist.
Критерій Найквіста
Критерій Найквіста дає графічний метод перевірки стійкості системи замкнутого контуру.
Припустимо, що\(G(s)\) має скінченну кількість нулів і полюсів у правій півплощині. Також припустимо, що\(G(s)\) розпадається до 0, як\(s\) переходить до нескінченності. Тоді система замкнутого контуру з\(k\) коефіцієнтом зворотного зв'язку стабільна тоді і тільки тоді, коли номер обмотки графіка Найквіста навколо\(w = -1\) дорівнює числу полюсів\(G(s)\) у правій півплощині.
Більш коротко,
\[G_{CL} (s) \text{ is stable } \Leftrightarrow \text{ Ind} (kG \circ \gamma, -1) = P_{G, RHP}\]
Ось уявна\(s\) -вісь і\(P_{G, RHP}\) кількість полюсів вихідної функції системи розімкнутого циклу\(G(s)\) в правій півплощині.\(\gamma\)
- Доказ
-
\(G_{CL}\)стійкий саме тоді, коли всі його полюси знаходяться в лівій півплощині. Тепер нагадаємо, що\(G_{CL}\) полюси - це саме нулі\(1 + k G\). Отже, стабільність\(G_{CL}\) - це саме умова, що кількість нулів\(1 + kG\) у правій півплощині дорівнює 0.
Давайте попрацюємо зі знайомим контуром.
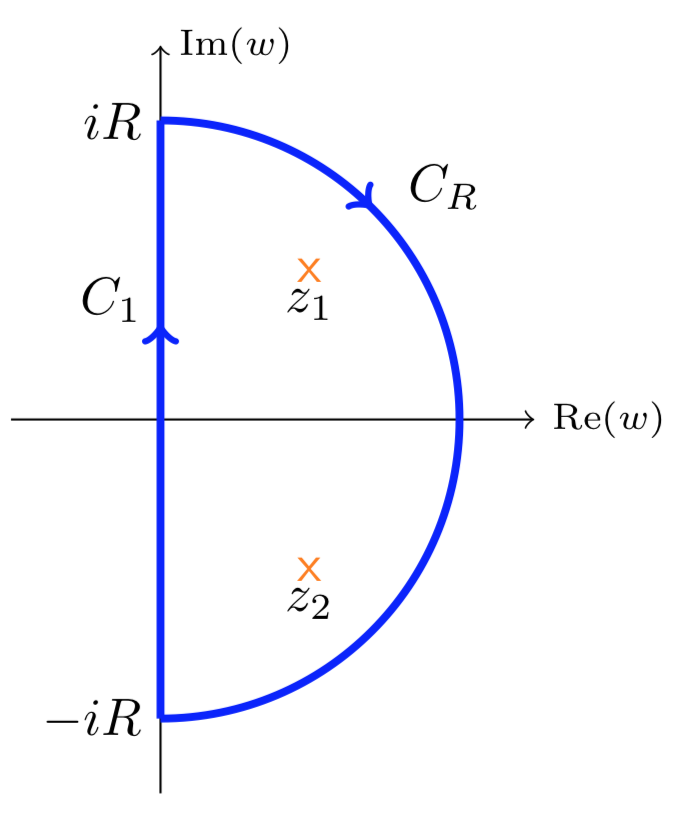
Нехай\(\gamma_R = C_1 + C_R\). Зверніть увагу,\(\gamma_R\) що проходить в\(clockwise\) напрямку. Виберіть досить\(R\) великий, щоб (кінцеве число) полюсів і нулів\(G\) у правій півплощині були всередині\(\gamma_R\). Тепер ми можемо застосувати Equation 12.2.4 в наслідок принципу аргументу\(\gamma\) до\(kG(s)\) і отримати
\[-\text{Ind} (kG \circ \gamma_R, -1) = Z_{1 + kG, \gamma_R} - P_{G, \gamma_R}\]
(Знак мінус - через напрямок кривої за годинниковою стрілкою.) Таким чином, для всіх великих\(R\)
\[\text{the system is stable } \Leftrightarrow \ Z_{1 + kG, \gamma_R} = 0 \ \Leftrightarow \ \text{ Ind} (kG \circ \gamma_R, -1) = P_{G, \gamma_R}\]
Нарешті, ми можемо\(R\) відпустити до нескінченності. Припущення, що\(G(s)\) розпадається 0 до як\(s\) йде,\(\infty\) означає, що в межі вся крива\(kG \circ C_R\) стає єдиною точкою на початку. Так в межі\(kG \circ \gamma_R\) стає\(kG \circ \gamma\). \(\text{QED}\)
Приклади використання математики Nyquist Plot
Критерій Nyquist - це візуальний метод, який вимагає певного способу створення сюжету Nyquist. Для цього ми будемо використовувати один з MIT Mathlets (трохи модифікований для наших цілей). Відкрийте аплет сюжету Nyquist за адресою
http://web.mit.edu/jorloff/www/jmoapplets/nyquist/nyquistCrit.html
Пограйте з аплетом, читайте довідку.
Тепер оновіть браузер, щоб відновити аплет в початковий стан. Встановіть\(Formula\) прапорець. Формула є простим способом зчитування значень полюсів і нулів\(G(s)\). У початковому стані аплет повинен мати нуль at\(s = 1\) і полюси в\(s = 0.33 \pm 1.75 i\).
Графік лівої руки - це діаграма полюс-нуль. Графік правої руки - це сюжет Nyquist.
Щоб відчути сюжет Nyquist. Подивіться на діаграму полюсів і за допомогою миші перетягніть жовту точку вгору і вниз по уявній осі. Його зображення під\(kG(s)\) простежить сюжет Нікіс.
Зверніть увагу, що коли жовта точка знаходиться на будь-якому кінці осі, її зображення на графіку Nyquist близьке до 0.
Оновіть сторінку, щоб повернути нуль і полюси в початковий стан. У правій півплощині є два полюси, тому система відкритого контуру\(G(s)\) нестабільна. З\(k =1\), який номер обмотки ділянки Nyquist навколо -1? Чи стабільна система замкнутого циклу?
Рішення
Крива накручується двічі навколо -1 в напрямку проти годинникової стрілки, тому число намотування\(\text{Ind} (kG \circ \gamma, -1) = 2\). Оскільки кількість полюсів\(G\) у правій півплощині таке ж, як це число обмоток, система замкнутого контуру стабільна.
З однаковими полюсами і нулями перемістіть\(k\) повзунок і визначте, який діапазон\(k\) робить систему замкнутого циклу стабільною.
Рішення
Коли\(k\) невеликий, сюжет Nyquist має обмотку номер 0 навколо -1. Для цих значень\(k\),\(G_{CL}\) є нестабільним. \(k = 0.7\)У міру\(k\) збільшення десь між\(k = 0.65\) і число обмоток скаче з 0 на 2 і система замкнутого контуру стає стабільною. Це триває до тих пір\(k\), поки не буде між 3. 10 і 3. 20, в цей момент число обмотки стає 1 і\(G_{CL}\) стає нестійким.
Відповідь: Система замкнутого циклу стабільна\(k\) (приблизно) між 0. 7 і 3. 10.
У попередній задачі ви могли б аналітично визначити діапазон\(k\),\(G_{CL} (s)\) де стабільний?
Рішення
Так! Це можливо для невеликих систем. Це складніше для систем вищого порядку, але є методи, які не вимагають обчислення полюсів. У цьому випадку ми маємо
\[G_{CL} (s) = \dfrac{G(s)}{1 + kG(s)} = \dfrac{\dfrac{s - 1}{(s - 0.33)^2 + 1.75^2}}{1 + \dfrac{k(s - 1)}{(s - 0.33)^2 + 1.75^2}} = \dfrac{s - 1}{(s - 0.33)^2 + 1.75^2 + k(s - 1)} \nonumber\]
Отже, полюси - коріння
\[(s - 0.33)^2 + 1.75^2 + k(s - 1) = s^2 + (k - 0.66)s + 0.33^2 + 1.75^2 - k \nonumber\]
Для квадратичного з додатними коефіцієнтами коріння мають негативну дійсну частину. Це відбувається, коли
\[0.66 < k < 0.33^2 + 1.75^2 \approx 3.17. \nonumber\]
Що відбувається, коли\(k\) переходить до 0.
Рішення
Що\(k\) стосується 0, графік Nyquist скорочується до однієї точки на початку. У цьому випадку число обмоток навколо -1 дорівнює 0, а критерій Найквіста говорить, що система замкнутого контуру стабільна тоді і лише тоді, коли система відкритого контуру стабільна.
Це має мати сенс, так як з\(k = 0\),
\[G_{CL} = \dfrac{G}{1 + kG} = G. \nonumber\]
Складіть систему з наступними нулями і полюсами:
- Пара нулів в\(0.6 \pm 0.75i\).
- Пара полюсів в\(-0.5 \pm 2.5i\).
- Один полюс на 0,25.
Чи стабільна відповідна система замкнутого циклу, коли\(k = 6\)?
Рішення
Відповідь - ні, не\(G_{CL}\) є стабільним. \(G\)має один полюс в правій половині площини. Матлет показує сюжет Nyquist вітрів один раз навколо\(w = -1\) в\(clockwise\) напрямку. Таким чином, число обмотки дорівнює -1, що не дорівнює числу полюсів\(G\) в правій півплощині.
Якщо ми встановимо\(k = 3\), система замкнутого контуру стабільна.
