12.1: Принцип аргументу

Last updated
Save as PDF

Page ID: 62701

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Налаштування

$\gamma$проста замкнута крива, орієнтована в напрямку проти годинникової стрілки. $f(z)$аналітичний на і всередині$\gamma$, за винятком (можливо) деяких скінченних полюсів всередині (не на)$\gamma$ і деяких нулів всередині (не на)$\gamma$.

Нехай$p_1, \ ..., p_m$ будуть полюси$f$ зсередини$\gamma$.
$z_1, \ ..., z_n$Дозволяти нулі$f$ всередині$\gamma$.
Запишіть mult$(z_k)$ = кратність нуля на$z_k$. Аналогічно запишіть mult ($p_k$) = порядок полюса в$p_k$.

Почнемо з теореми, яка призведе до принципу аргументу.

Теорема$\PageIndex{1}$

З вищевказаною налаштуванням

\[\int_{\gamma} \dfrac{f'(z)}{f(z)} \ dz = 2\pi i (\sum \text{mult} (z_k) - \sum \text{mult} (p_k)).\]

Доказ

Щоб довести цю теорему, нам потрібно зрозуміти полюси і залишки$f'(z)/f(z)$. Маючи це на увазі, припустимо,$f(z)$ має нуль порядку$m$ в$z_0$. Серія Тейлора для$f(z)$$z_0$ ближнього

\[f(z) = (z - z_0)^m g(z)\]

де$g(z)$ аналітичний і ніколи не 0 на невеликій околиці$z_0$. Це має на увазі

\[\begin{array} {rcl} {\dfrac{f'(z)}{f(z)}} & = & {\dfrac{m(z - z_0)^{m - 1} g(z) + (z - z_0)^m g'(z)}{(z - z_0)^m g(z)}} \\ {} & = & {\dfrac{m}{z - z_0} + \dfrac{g'(z)}{g(z)}} \end{array}\]

Оскільки ніколи$g(z)$ не 0,$g'(z)/g(z)$ є аналітичним поруч$z_0$. Це означає, що$z_0$ це простий полюс$f'(z)/f(z)$ і

\[\text{Res} (\dfrac{f'(z)}{f(z)}, z_0) = m \text{mult} (z_0).\]

Так само, якщо$z_0$ це полюс порядку,$m$ то серія Лорана для$f(z)$$z_0$ ближнього

\[f(z) = (z - z_0)^{-m} g(z)\]

де$g(z)$ аналітичний і ніколи не 0 на невеликій околиці$z_0$. Таким чином,

\[\begin{array} {rcl} {\dfrac{f'(z)}{f(z)}} & = & {-\dfrac{m(z - z_0)^{-m - 1} g(z) + (z - z_0)^{-m} g'(z)}{(z - z_0)^{-m} g(z)}} \\ {} & = & {-\dfrac{m}{z - z_0} + \dfrac{g'(z)}{g(z)}} \end{array}\]

Знову ми маємо, що$z_0$ це простий полюс$f'(z)/f(z)$ і

\[\text{Res} (\dfrac{f'(z)}{f(z)}, z_0) = -m = -\text{mult} (z_0).\]

Теорема тепер випливає відразу з теореми про залишок:

\[\begin{array} {rcl} {\int_{\gamma} \dfrac{f'(z)}{f(z)} \ dz} & = & {2\pi i \text{ sum of the residues}} \\ {} & = & {2\pi i (\sum \text{mult} (z_k) - \sum \text{mult} (p_k)).} \end{array}\]

Визначення

$Z_{f, \gamma}$Запишемо на суму кратностей нулів$f$ всередині$\gamma$. Аналогічно для$P_{f, \gamma}$. Отже, теорема 12.2.1 говорить:

\[\int_{\gamma} \dfrac{f'}{f} \ dz = 2\pi i (Z_{f, \gamma} - P_{f, \gamma}).\]

Визначення: Номер обмотки

У нас є інтуїція до того, що це означає. Ми визначаємо його формально за формулою Коші. Якщо$\gamma$ замкнута крива, то її номер обмотки (або індекс) про$z_0$ визначається як

\[\text{Ind} (\gamma, z_0) = \dfrac{1}{2\pi i} \int_{\gamma} \dfrac{1}{z - z_0}\ dz.\]

Картографування кривих:$f \circ \gamma$

Одне з ключових понять у цій темі - відображення однієї кривої на іншу. Тобто якщо$z = \gamma (t)$ крива і$w = f(z)$ є функцією, то$w = f \circ \gamma (t) = f(\gamma (t))$ інша крива. Ми говоримо, що$f$ карти$\gamma$ до$f \circ \gamma$. Ми робили це часто в минулому, але це досить важливо для нас зараз, щоб ми зупинимося на цьому і наведемо кілька прикладів. Це ключове поняття в принципі аргументу, і ви повинні переконатися, що вам дуже зручно з ним.

Приклад$\PageIndex{1}$

Нехай$\gamma (t) = e^{it}$ з$0 \le t \le 2\pi$ (одиниця кола). Нехай$f(z) = z^2$. Опишіть криву$f \circ \gamma$.

Рішення

$f \circ \gamma (t) = e^{2it}$Чітко$t$ проходить одиничне коло вдвічі більше, ніж від 0 до$2\pi$.

Приклад$\PageIndex{2}$

Нехай$\gamma (t) = it$ з$-\infty < t < \infty$ ($y$-вісь). Нехай$f(z) = 1/(z + 1)$. Опишіть криву$f \circ \gamma (t)$.

Рішення

$f(z)$є дробовим лінійним перетворенням і відображає$\gamma$ лінію, задану колом, через початок з центром у 12. Здійснивши перевірку в декількох точках:

$f(-i) = \dfrac{1}{-i + 1} = \dfrac{1 + i}{2}$,$f(0) = 1$,$f(i) = \dfrac{1}{i + 1} = \dfrac{1 - i}{2}$,$f(\infty) = 0$.

Ми бачимо, що коло проходить за годинниковою стрілкою, як$t$ йде від$-\infty$ до$\infty$.

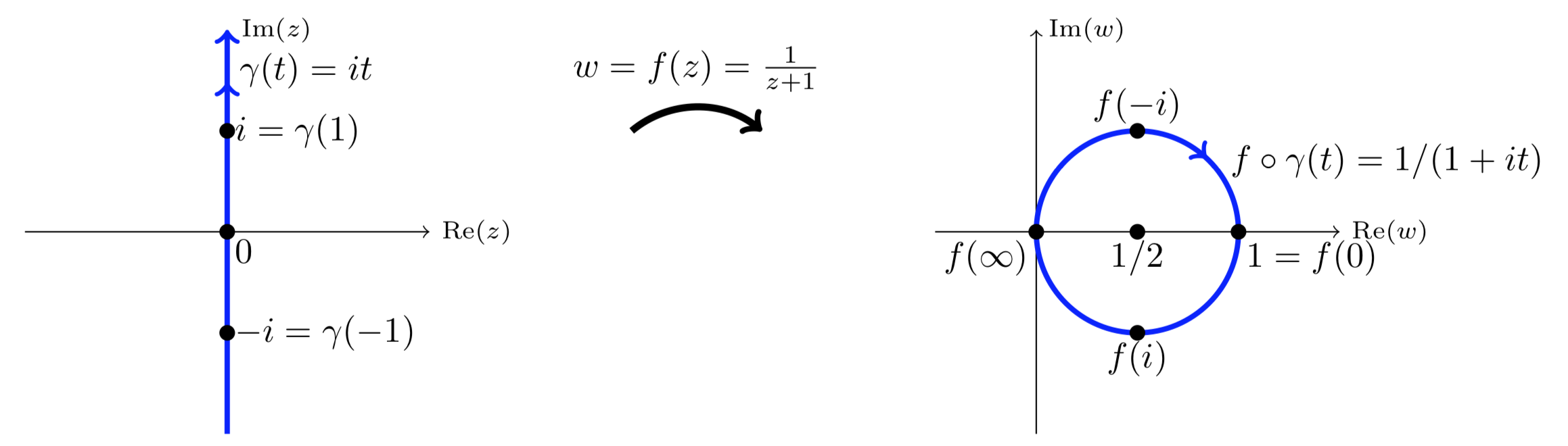
$2020-09-14 3.11.36.png$
Крива$z = \gamma (t) = it$ відображається на$w = f \circ \gamma (t)) = 1/(it + 1).$

Принцип аргументу

Ви також побачите, що це називається принципом аргументу.

Теорема$\PageIndex{2}$ Argument principle

Для$f$ та$\gamma$ з тією ж налаштуванням, що і вище

\[\int_{\gamma} \dfrac{f'(z)}{f(z)}\ dz = 2\pi i \text{Ind} (f \circ \gamma, 0) = 2\pi i (Z_{f, \gamma} - P_{f, \gamma})\]

Доказ

Теорема 12.2.1 показала, що

\[\int_{\gamma} \dfrac{f'(z)}{f(z)}\ dz = 2\pi i (Z_{f, \gamma} - P_{f, \gamma})\]

Таким чином, ми повинні показати, що інтеграл також дорівнює число обмотки дано. Це просто зміна змінних$w = f(z)$. З цією зміною змінних лічильник$z = \gamma (t)$ стає$w = f \circ \gamma (t)$ і$dw = f'(z)\ dz$ так

\[\int_{\gamma} \dfrac{f'(z)}{f(z)}\ dz = \int_{f \circ \gamma} \dfrac{dw}{w} = 2\pi i \text{Ind} (f \circ \gamma, 0)\]

Останнє рівність у вищевказаному рівнянні походить від визначення числа обмоток.

Зверніть увагу, що за припущенням$\gamma$ не проходить через будь-які нулі$f$, тому ніколи не$w = f(\gamma (t))$ дорівнює нулю і$1/w$ в інтегралі не проблема.

Ось легкий наслідок принципу аргументу, який стане в нагоді нам пізніше.

Слідство

Припустімо, що$f \circ \gamma$ не проходить −1, тобто немає нулів$1 + f(z)$ on$\gamma$ тоді

\[\int_{\gamma} \dfrac{f'}{f + 1} = 2\pi i \text{Ind}(f \circ \gamma, -1) = 2\pi i (Z_{1 + f, \gamma} - P_{f, \gamma}).\]

Доказ

Застосовуючи принцип аргументу в Рівнянні 12.2.11 до функції$1 + f(z)$, отримаємо

\[\int_{\gamma} \dfrac{(1 + f)' f(z)}{1 + f(z)} \ dz = 2\pi i \text{Ind} (1 + f \circ \gamma, 0) = 2\pi i (Z_{1 + f, \gamma} - P_{1 + f, \gamma}) \nonumber\]

Тепер ми можемо порівняти кожен з членів цього рівняння з тими, що знаходяться в Рівнянні 12.2.14:

\[\begin{array} {rclcl} {\int_{\gamma} \dfrac{(1 + f)' f(z)}{1 + f(z)} \ dz} & = & {\int_{\gamma} \dfrac{f' f(z)}{1 + f(z)} \ dz} & \ \ & {(\text{because } (1 + f)' = f')} \\ {\text{Ind} (1 + f \circ \gamma, 0)} & = & {\text{Ind} (f \circ \gamma, -1)} & \ \ & {(1 + f \text{ winds around 0 } \Leftrightarrow \text{ winds around -1})} \\ {Z_{1 + f, \gamma}} & = & {Z_{1 + f, \gamma}} & \ \ & {(\text{same in both equation}))} \\ {P_{1 + f, \gamma}} & = & {P_{f, \gamma}} & \ \ & {(\text{poles of } f = \text{poles of } 1 + f)} \end{array}\]

Приклад$\PageIndex{3}$

Нехай$f(z) = z^2 + z$ Знайти номер обмотки$f \circ \gamma$ близько 0 для кожної з наступних кривих.

$\gamma_1$= коло радіуса 2.
$\gamma_2$= коло радіуса 1/2.
$\gamma_3$= коло радіуса 1.

Рішення

$f(z)$має нулі при 0, −1. Він не має полюсів.

Отже, не$f$ має полюсів і двох нулів всередині$\gamma_1$. Принцип аргументу говорить$\text{Ind} (f \circ \gamma_1 , 0) = Z_{f, \gamma_1} - P_{f, \gamma} = 2$

Аналогічно не$f$ має полюсів і один нуль всередині$\gamma_2$, тому$\text{Ind} (f \circ \gamma_2, 0) = 1 - 0 = 1$

Для$\gamma_3$ нуля$f$ знаходиться на кривій, тобто$f(-1) = 0$, тому принцип аргументу не застосовується. Зображення$\gamma_3$ показано на малюнку нижче — воно проходить через 0.

$2020-09-15 2.14.35.png$
Зображення 3-х різних кіл під$f(z) = z^2 + z$.

Теорема Руше

Теорема$\PageIndex{3}$: Rouché’s theorem

Зробіть наступні припущення:

$\gamma$являє собою просту замкнуту криву
$f, h$є аналітичними функціями всередині і всередині$\gamma$, за винятком деяких скінченних полюсів.
Тут немає полюсів$f$ і$h$ на$\gamma$.
$|h| < |f|$всюди на$\gamma$.

Тоді

\[\text{Ind} (f \circ \gamma, 0) = \text{Ind} ((f + h) \circ \gamma, 0).\]

Тобто,

\[Z_{f, \gamma} - P_{f, \gamma} = Z_{f + h, \gamma} - P_{f + h, \gamma}\]

Доказ

На заняттях ми дали евристичний доказ за участю людини, що вигулює собаку навколо$f \circ \gamma$ на повідку довжини$h \circ \gamma$. Ось аналітичний доказ.

Принцип аргументу вимагає, щоб функція не мала нулів або полюсів$\gamma$. Отже, ми спочатку покажемо, що це вірно$f, f + h, (f + h)/f$. Аргумент йде наступним чином.

Нулі: Той факт, що$0 \le |h| < |f|$ on$\gamma$ означає, що не$f$ має нулів$\gamma$. Це також означає, що не$f + h$ має нулів$\gamma$, оскільки значення ніколи не$h$ є достатньо великим, щоб скасувати це$f$. Так як$f$ і не$f + h$ мають нулів, ні$(f + h)/f$.

Поляки: За припущенням$f$ і не$h$ мають полюсів на$\gamma$, тому не$f + h$ має там полюсів. Так як не$f$ має нулів$\gamma$ увімкнено, не$(f + h)/f$ має там полюсів.

Тепер ми можемо застосувати принцип аргументу до$f$ і$f + h$

\[\dfrac{1}{2\pi i} \int_{\gamma} \dfrac{f'}{f} \ dz = \text{Ind} (f \circ \gamma, 0) = Z_{f, \gamma} - P_{f, \gamma}.\]

\[\dfrac{1}{2\pi i} \int_{\gamma} \dfrac{(f + h)'}{f + h} \ dz = \text{Ind} ((f + h) \circ \gamma, 0) = Z_{f + h, \gamma} - P_{f + h, \gamma}.\]

Далі, за припущенням$|\dfrac{h}{f}| < 1$, так$(\dfrac{h}{f}) \circ \gamma$ знаходиться всередині одиничного кола. Це означає, що$1 + \dfrac{h}{f} = \dfrac{f + h}{f}$$\gamma$ відображає внутрішню частину одиничного диска з центром 1. (Для цього слід намалювати фігуру.) Це означає, що

\[\text{Ind} ((\dfrac{f + h}{f}) \circ \gamma, 0) = 0.\]

Нехай$g = \dfrac{f + h}{f}$. Вище сказано$\text{Ind} (g \circ \gamma, 0) = 0$. Отже,$\int_{\gamma} \dfrac{g'}{g} \ dz = 0$. (Ми показали вище, що не$g$ має нулів або полюсів$\gamma$.)

Тепер це легко обчислити$\dfrac{g'}{g} = \dfrac{(f + h)'}{f + h} - \dfrac{f'}{f}$. Отже, використовуючи

\[\text{Ind} (g \circ \gamma, 0) = \int_{\gamma} \dfrac{g'}{g}\ dz = \int_{\gamma} \dfrac{(f + h)'}{f + h} \ dz - \int_{\gamma} \dfrac{f'}{f} \ dz = 0 \Rightarrow \text{Ind} ((f + h) \circ \gamma, 0) = \text{Ind} (f \circ \gamma, 0).\]

Тепер рівняння 12.2.19 і 12.2.20 розповідають нам$Z_{f, \gamma} - P_{f, \gamma} = Z_{f + h, \gamma} - P_{f + h, \gamma}$, тобто ми довели теорему Руше.

Слідство

За тими ж гіпотезами, якщо$h$ і$f$ є аналітичними (без полюсів), то

\[Z_{f, \gamma} = Z_{f + h, \gamma}.\]

Доказ: Так як функції аналітичні$P_{f, \gamma}$ і$P_{f + h, \gamma}$ обидва 0. Отже, рівняння 12.2.18 показує$Z_f = Z_{f + h}$. $\text{QED}$

Ми вважаємо невеликим збуренням$f$.$h$

Приклад$\PageIndex{4}$

Показати всі 5 нулів$z^5 + 3z + 1$ знаходяться всередині кривої$C_2: |z| = 2$.

Рішення

Нехай$f(z) = z^5$ і$h(z) = 3z + 1$. Зрозуміло, що всі 5 коренів$f$ (дійсно один корінь з кратністю 5) знаходяться всередині$C_2$. Також зрозуміло,$|h| < 7 < 32 = |f|$ на$C_2$. Наслідок теореми Руше говорить, що всі 5 коренів також$f + h = z^5 + 3z + 1$ повинні бути всередині кривої.

Приклад$\PageIndex{5}$

Show$z + 3 + 2e^z$ має один корінь у лівій півплощині.

Рішення

Нехай$f(z) = z + 3$,$h(z) = 2e^z$. Розглянемо контур від$-iR$ до$iR$ вздовж$y$ -осі, а потім ліве півколо радіуса$R$ назад до$-iR$. Тобто контур,$C_1 + C_R$ показаний нижче.

$2020-09-15 2, 41.51.понг$

Щоб застосувати наслідок теореми Руше, нам потрібно перевірити, що (для$R$ великих)$|h| < |f|$$C_1 + C_R$. На$C_1$$z = iy$, так

\[|f(z)| = |3 + iy| \ge 3, \ \ \ |h(z)| = 2|e^{iy}| = 2.\]

Так$|h| < |f|$ далі$C_1$.

На$C_R$,$z = x + iy$ з$x < 0$ і$|z| = R$. Отже,

\[|f(z)| > R - 3 \text{ for } R \text{ large, } |h(z)| = 2|e^{x + iy}| = 2e^x < 2 \text{ (since } x < 0).\]

Так$|h| < |f|$ далі$C_R$.

Єдиний нуль$f$ ia at$z = -3$, який лежить всередині контуру.

Тому, за теоремою Слідство Руше,$f + h$ має таку ж кількість коренів, як і$f$ всередині контуру, тобто 1. Тепер$R$ відпускаємо до нескінченності, і ми бачимо, що$f + h$ має тільки один корінь у всій півплощині.

Теорема$\PageIndex{4}$: Fundamental Theorem of Algebra

Теорема Руше може бути використана для доведення фундаментальної теореми алгебри наступним чином.

Доказ

Нехай

\[P(z) = z^n + a_{n - 1} z^{n - 1} + \ ... + a_0\]

be$n$ і порядковий многочлен. Нехай$f(z) = z^n$ і$h = P - f$. Вибирайте$R$ таку, що$R > \text{max} (1, n |a_{n - 1}|, ..., n|a_0|)$. Тоді на$|z| = R$ нас

\[|h| \le |a_{n - 1}| R^{n - 1} + |a_{n - 2}| R^{n - 2} + \ ... + |a_0| \le \dfrac{R}{n} R^{n - 1} + \dfrac{R}{n} R^{n - 2} + \ ... + \dfrac{R}{n} < R^n.\]

На$|z| = R$ нас є$|f(z)| = R^n$, так що ми показали$|h| < |f|$ на кривій. Таким чином, наслідок теореми Руше говорить$f + h$ і$f$ має однакову кількість нулів всередині$|z| = R$. Оскільки ми знаємо, що$f$ має точно$n$ нулі всередині кривої те ж саме вірно для многочлена$f + h$. Тепер$R$ відпустіть до нескінченності, ми показали, що$f + h$ має рівно$n$ нулі у всій площині.

Примітка

Доказ дає просту прив'язку до розміру нулів: всі вони мають величину менше або дорівнює$\text{max} (1, n |a_{n - 1}|, ..., n|a_0|)$.

Теорема\(\PageIndex{1}\)