5.1: Обмеження

Нехай$A \subset \mathbb{R}$ і нехай$x$ буде граничною точкою$A .$ в наступному, ми дозволимо$S(A, x)$ позначити набір всіх збігаються послідовностей$\left\{x_{n}\right\}_{n \in I}$ такі, що$x_{n} \in A$ для всіх$n \in I, x_{n} \neq x$ для всіх$n \in I,$ і$\lim _{n \rightarrow \infty} x_{n}=x .$ Ми дозволимо$S^{+}(A, x)$ бути підмножиною$S(A, x)$ послідовностей $\left\{x_{n}\right\}_{n \in I}$для яких$x_{n}>x$ для всіх$n \in I$ і$S^{-}(A, x)$ бути підмножиною$S(A, x)$ послідовностей,$\left\{x_{n}\right\}_{n \in I}$ для яких$x_{n}<x$ для всіх$n \in I .$

Визначення

Нехай$D \subset \mathbb{R}, f: D \rightarrow \mathbb{R}, L \in \mathbb{R},$ і припустимо$a$ є граничною точкою$D .$ Ми говоримо$f$ межа як$x$ підходів$a$$L,$ позначається

$$\lim _{x \rightarrow a} f(x)=L ,$$

якщо для кожної послідовності$\left\{x_{n}\right\}_{n \in I} \in S(D, a)$,

$$\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L .$$

Якщо$S^{+}(D, a) \neq \emptyset,$ говорити межа з правого боку$f$ як$x$ підходи$a$$L,$ позначається

$$\lim _{x \rightarrow a+} f(x)=L ,$$

якщо для кожної послідовності$\left\{x_{n}\right\}_{n \in I} \in S^{+}(D, a)$,

$$\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L ,$$

і, якщо$S^{-}(D, a) \neq \emptyset,$ говорити ліміт зліва від$f$ як$x$ підходи$a$$L,$ позначається

$$\lim _{x \rightarrow a-} f(x)=L ,$$

якщо для кожної послідовності$\left\{x_{n}\right\}_{n \in I} \in S^{-}(D, a)$,

$$\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L .$$

Ми також можемо позначити

$$\lim _{x \rightarrow a} f(x)=L$$

шляхом написання

$$f(x) \rightarrow L \text { as } x \rightarrow a .$$

Аналогічно ми можемо позначити

$$\lim _{x \rightarrow a^{+}} f(x)=L$$

шляхом написання

$$f(x) \rightarrow L \text { as } x \downarrow a$$

і

$$\lim _{x \rightarrow a^{-}} f(x)=L$$

шляхом написання

$$f(x) \rightarrow L \text { as } x \uparrow a$$

Ми також дозволяємо

$$f(a+)=\lim _{x \rightarrow a^{+}} f(x)$$

і

$$f(a-)=\lim _{x \rightarrow a^{-}} f(x).$$

Повинно бути зрозуміло, що якщо$\lim _{x \rightarrow a} f(x)=L$ і$S^{+}(D, a) \neq \emptyset,$ то$f(a+)=L$. Аналогічно, якщо$\lim _{x \rightarrow a} f(x)=L$ і$S^{-}(D, a) \neq \emptyset,$ то$f(a-)=L$.

Пропозиція$\PageIndex{1}$

Припустимо$a$,$D \subset \mathbb{R}, f: D \rightarrow \mathbb{R},$ і є граничною точкою$D$. Якщо$f(a-)=f(a+)=L,$ тоді$\lim _{x \rightarrow a} f(x)=L$.

Доказ

Припустимо,$\left\{x_{n}\right\}_{n=m}^{\infty} \in S(D, a) .$ нехай

$$J^{-}=\left\{n: n \in \mathbb{Z}, x_{n}<a\right\}$$

і

$$J^{+}=\left\{n: n \in \mathbb{Z}, x_{n}>a\right\}.$$

Припустимо,$J^{-}$ порожній або кінцевий і нехай$k=m-1$ якщо$J^{-}=\emptyset$ і, в іншому випадку, нехай$k$ буде найбільше ціле число в$J^{-} .$ Тоді$\left\{x_{n}\right\}_{n=k+1}^{\infty} \in S^{+}(D, a),$ і так

$$\lim _{n \rightarrow \infty} f\left(x_{n}\right)=f(a+)=L.$$

Аналогічний аргумент показує,$J^{+}$ що якщо порожній або кінцевий, то

$$\lim _{n \rightarrow \infty} f\left(x_{n}\right)=f(a-)=L.$$

Якщо ні$J^{-}$ ні$J^{+}$ є скінченним або порожнім, то$\left\{x_{n}\right\}_{n \in J}-$ і$\left\{x_{n}\right\}_{n \in J}+$ є підпослідовностями$\left\{x_{n}\right\}_{n=m}^{\infty}$ з$\left\{x_{n}\right\}_{n \in J^{-}} \in S^{-}(D, a)$ і$\left\{x_{n}\right\}_{n \in J+} \in S^{+}(D, a) .$ Отже, задано будь-яке,$\epsilon>0,$ ми можемо знайти цілі числа$N$ і$M$ такі, що

$$\left|f\left(x_{n}\right)-L\right|<\epsilon$$

всякий раз$n \in\left\{j: j \in J^{-}, j>N\right\}$ і

$$\left|f\left(x_{n}\right)-L\right|<\epsilon$$

всякий раз, коли$n \in\left\{j: j \in J^{+}, j>M\right\} .$$P$ Дозволяти бути більшим$M .$ з$N$ і Оскільки$J^{-} \cup J^{+}=\left\{j: j \in \mathbb{Z}^{+}, j \geq m\right\},$ випливає, що

$$\left|f\left(x_{n}\right)-L\right|<\epsilon$$

всякий раз, коли$n>P .$ Звідси$\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L,$ і так$\lim _{x \rightarrow a} f(x)=L$. $\quad$Q.E.D.

Пропозиція$\PageIndex{2}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D,$ і$f: D \rightarrow \mathbb{R}$. Якщо$\lim _{x \rightarrow a} f(x)=L$ і$\alpha \in \mathbb{R},$ тоді

$$\lim _{x \rightarrow a} \alpha f(x)=\alpha L.$$

Доказ

Припустимо$\left\{x_{n}\right\}_{n \in I} \in S(D, a) .$, тоді

$$\lim _{n \rightarrow \infty} \alpha f\left(x_{n}\right)=\alpha \lim _{n \rightarrow \infty} f\left(x_{n}\right)=\alpha L.$$

Звідси$\lim _{x \rightarrow a} \alpha f(x)=\alpha L$. $\quad$Q.E.D.

Пропозиція$\PageIndex{3}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D, f: D \rightarrow \mathbb{R},$ і$g: D \rightarrow \mathbb{R} .$ якщо,$\lim _{x \rightarrow a} f(x)=L$ а$\lim _{x \rightarrow a} g(x)=M,$ потім

$$\lim _{x \rightarrow a}(f(x)+g(x))=L+M.$$

Доказ

Припустимо$\left\{x_{n}\right\}_{n \in I} \in S(D, a) .$, тоді

$$\lim _{n \rightarrow \infty}\left(f\left(x_{n}\right)+g\left(x_{n}\right)\right)=\lim _{n \rightarrow \infty} f\left(x_{n}\right)+\lim _{n \rightarrow \infty} g\left(x_{n}\right)=L+M.$$

Звідси$\lim _{x \rightarrow a}(f(x)+g(x))=L+M$. $\quad$Q.E.D.

Пропозиція$\PageIndex{4}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D, f: D \rightarrow \mathbb{R},$ і$g: D \rightarrow \mathbb{R} .$ якщо,$\lim _{x \rightarrow a} f(x)=L$ а$\lim _{x \rightarrow a} g(x)=M,$ потім

$$\lim _{x \rightarrow a} f(x) g(x)=L M.$$

Вправа$\PageIndex{1}$

Доведіть попередню пропозицію.

Пропозиція$\PageIndex{5}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D, f: D \rightarrow \mathbb{R}$,$g: D \rightarrow \mathbb{R},$ і$g(x) \neq 0$ для всіх$x \in D .$ Якщо$\lim _{x \rightarrow a} f(x)=L, \lim _{x \rightarrow a} g(x)=M,$ і$M \neq 0,$ тоді

$$\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{L}{M}.$$

Вправа$\PageIndex{2}$

Доведіть попередню пропозицію.

Пропозиція$\PageIndex{6}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D, f: D \rightarrow \mathbb{R},$ і$f(x) \geq 0$ для всіх$x \in D .$ Якщо$\lim _{x \rightarrow a} f(x)=L,$ тоді

$$\lim _{x \rightarrow a} \sqrt{f(x)}=\sqrt{L}.$$

Вправа$\PageIndex{3}$

Доведіть попередню пропозицію.

Дано$D \subset \mathbb{R}, f: D \rightarrow \mathbb{R},$ і$A \subset D,$ ми нехай

$$f(A)=\{y: y=f(x) \text { for some } x \in A\}.$$

Зокрема,$f(D)$ позначає діапазон$f$.

Пропозиція$\PageIndex{7}$

Припустимо,$D \subset \mathbb{R}, E \subset \mathbb{R}, a$ це гранична точка$D, g: D \rightarrow \mathbb{R}$,$f: E \rightarrow \mathbb{R},$ і$g(D) \subset E .$ Більш того, припустимо$\lim _{x \rightarrow a} g(x)=b$ і, для деяких$\epsilon>0$,$g(x) \neq b$ для всіх$x \in(a-\epsilon, a+\epsilon) \cap D .$ Якщо$\lim _{x \rightarrow b} f(x)=L,$ тоді

$$\lim _{x \rightarrow a} f \circ g(x)=L.$$

Доказ

Припустимо$\left\{x_{n}\right\}_{n \in I} \in S(D, a) .$, тоді

$$\lim _{n \rightarrow \infty} g\left(x_{n}\right)=b.$$

Нехай$N \in \mathbb{Z}^{+}$ таке, що$\left|x_{n}-a\right|<\epsilon$ всякий раз$n>N .$ тоді

$$\left\{g\left(x_{n}\right)\right\}_{n=N+1}^{\infty} \in S(E, b),$$

тому

$$\lim _{n \rightarrow \infty} f\left(g\left(x_{n}\right)\right)=L.$$

Таким чином$\lim _{x \rightarrow a} f \circ g(x)=L$. $\quad$Q.E.D.

Приклад$\PageIndex{1}$

Нехай

$$g(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x \neq 0,} \\ {1,} & {\text { if } x=0.}\end{array}\right.$$

Якщо$f(x)=g(x),$ тоді

$$f \circ g(x)=\left\{\begin{array}{ll}{1,} & {\text { if } x \neq 0,} \\ {0,} & {\text { if } x=0.}\end{array}\right.$$

Звідси$\lim _{x \rightarrow 0} f \circ g(x)=1,$ хоча$\lim _{x \rightarrow 0} g(x)=0$ і$\lim _{x \rightarrow 0} f(x)=0$.

5.1.1 Межі поліномів і раціональних функцій

Приклад$\PageIndex{2}$

Якщо$c \in \mathbb{R}$ і$f: \mathbb{R} \rightarrow \mathbb{R}$ дається$f(x)=c$ для всіх$x \in \mathbb{R}$, то явно$\lim _{x \rightarrow a} f(x)=c$ для будь-якого$a \in \mathbb{R}$.

Приклад$\PageIndex{3}$

Припустимо,$f: \mathbb{R} \rightarrow \mathbb{R}$ визначається$f(x)=x$ для всіх$x \in \mathbb{R} .$ If, для будь-якого$a \in \mathbb{R},\left\{x_{n}\right\}_{n \in I} \in S(\mathbb{R}, a),$ тоді

$$\lim _{n \rightarrow \infty} f\left(x_{n}\right)=\lim _{n \rightarrow \infty} x_{n}=a.$$

Звідси$\lim _{x \rightarrow a} x=a$.

Приклад$\PageIndex{4}$

$f: \mathbb{R} \rightarrow \mathbb{R}$Припустимо$n \in \mathbb{Z}^{+}$ і визначається$f(x)=x^{n}$. Тоді

$$\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} x^{n}=\prod_{i=1}^{n} \lim _{x \rightarrow a} x=a^{n}.$$

Визначення

Якщо$n \in \mathbb{Z}, n \geq 0,$ і$b_{0}, b_{1}, \ldots, b_{n}$ є дійсними числами,$b_{n} \neq 0,$ то ми викликаємо функцію,$p: \mathbb{R} \rightarrow \mathbb{R}$ визначену

$$p(x)=b_{n} x^{n}+b_{n-1} x^{n-1}+\cdots+b_{1} x+b_{0}$$

многочлен ступеня$n$.

Вправа$\PageIndex{4}$

Покажіть, що якщо$f$ є многочленом, а$a \in \mathbb{R},$ потім$\lim _{x \rightarrow a} f(x)=f(a)$.

Визначення

Припустимо$q$,$p$ і є поліномами і

$$D=\{x: x \in \mathbb{R}, q(x) \neq 0\}.$$

Викликаємо функцію,$r: D \rightarrow \mathbb{R}$ визначену

$$r(x)=\frac{p(x)}{q(x)}$$

раціональна функція.

Вправа$\PageIndex{5}$

Показати, що$f$ if є раціональною функцією і$a$ знаходиться в області$f,$ тоді$\lim _{x \rightarrow a} f(x)=f(a)$.

Вправа$\PageIndex{6}$

Припустимо,$D \subset \mathbb{R}, a \in D$ це гранична точка$D,$ і$\lim _{x \rightarrow a} f(x)=L$. Якщо$E=D \backslash\{a\}$ і$g: E \rightarrow \mathbb{R}$ визначається$g(x)=f(x)$ для всіх$x \in E,$ показати, що$\lim _{x \rightarrow a} g(x)=L .$

Вправа$\PageIndex{7}$

Оцінити

$$\lim _{x \rightarrow 1} \frac{x^{5}-1}{x^{3}-1}.$$

Вправа$\PageIndex{8}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D, f: D \rightarrow \mathbb{R}, g: D \rightarrow \mathbb{R}$,$h: D \rightarrow \mathbb{R},$ і$f(x) \leq h(x) \leq g(x)$ для всіх$x \in D .$ Якщо$\lim _{x \rightarrow a} f(x)=L$ і$\lim _{x \rightarrow a} g(x)=L,$ показати, що$\lim _{x \rightarrow a} h(x)=L .$ (Це теорема стиснення для меж функцій.)

Зауважте, що наведені вище результати, які були вказані для лімітів, також будуть мати відповідні односторонні межі, тобто обмеження праворуч або ліворуч.

Вправа$\PageIndex{9}$

Припустимо

$$f(x)=\left\{\begin{array}{ll}{x+1,} & {\text { if } x<0,} \\ {4,} & {\text { if } x=0,} \\ {x^{2},} & {\text { if } x>0.}\end{array}\right.$$

Оцініть$f(0), f(0-),$ і$f(0+) .$ чи$\lim _{x \rightarrow 0} f(x)$ існує?

5.1.2 Еквівалентні визначення

Пропозиція$\PageIndex{8}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D,$ і$f: D \rightarrow \mathbb{R}$. Тоді$\lim _{x \rightarrow a} f(x)=L$ якщо і тільки якщо для кожного$\epsilon>0$ існує$\delta>0$ таке, що

$$|f(x)-L|<\epsilon \text { whenever } x \neq a \text { and } x \in(a-\delta, a+\delta) \cap D.$$

Доказ

$\lim _{x \rightarrow a} f(x)=L .$Припустимо, існує$\epsilon>0$ таке, що для кожного$\delta>0$ існує$x \in(a-\delta, a+\delta) \cap D, x \neq a,$ для якого$|f(x)-L| \geq \epsilon$. Для$n=1,2,3, \ldots,$ вибору

$$x_{n} \in\left(a-\frac{1}{n}, a+\frac{1}{n}\right) \cap D,$$

$x_{n} \neq a,$такий, що$\left|f\left(x_{n}\right)-L\right| \geq \epsilon .$ Тоді$\left\{x_{n}\right\}_{n=1}^{\infty} \in S(D, a),$ але$\left\{f\left(x_{n}\right)\right\}_{n=1}^{\infty}$ не сходиться, щоб$L,$ суперечити припущенню, що$\lim _{x \rightarrow a} f(x)=L$.

Тепер припустимо, що для кожного$\epsilon>0$ існує$\delta>0$ таке, що$|f(x)-L|<\epsilon$ всякий раз$x \neq a$ і$x \in(a-\delta, a+\delta) \cap D .$ нехай$\left\{x_{n}\right\}_{n \in I} \in S(D, a) .$ дано$\epsilon>0$, нехай$\delta>0$ буде таким, що$|f(x)-L|<\epsilon$ всякий раз$x \neq a$ і$x \in(a-\delta, a+\delta) \cap D .$ Вибирайте$N \in \mathbb{Z}$ такий, що$\left|x_{n}-a\right|<\delta$ коли б$n>N .$ то $\left|f\left(x_{n}\right)-L\right|<\epsilon$для всіх$n>N .$ Отже$\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L,$ і так$\lim _{x \rightarrow a} f(x)=L .$$\quad$ Q.E.D.

Докази наступних двох суджень аналогічні.

Пропозиція$\PageIndex{9}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D, f: D \rightarrow \mathbb{R},$ і$S^{-}(D, a) \neq \emptyset .$ тоді,$\lim _{x \rightarrow a^{-}} f(x)=L$ якщо і тільки якщо для кожного$\epsilon>0$ існує$\delta>0$ така, що

$$|f(x)-L|<\epsilon \text { whenever } x \in(a-\delta, a) \cap D.$$

Пропозиція$\PageIndex{10}$

Припустимо,$D \subset \mathbb{R}, a$ це гранична точка$D, f: D \rightarrow \mathbb{R},$ і$S^{+}(D, a) \neq \emptyset .$ тоді,$\lim _{x \rightarrow a^{+}} f(x)=L$ якщо і тільки якщо для кожного$\epsilon>0$ існує$\delta>0$ така, що

$$|f(x)-L|<\epsilon \text { whenever } x \in(a, a+\delta) \cap D.$$

5.1.3 Приклади

Приклад$\PageIndex{5}$

Визначте$f: \mathbb{R} \rightarrow \mathbb{R}$ по

$$f(x)=\left\{\begin{array}{ll}{1,} & {\text { if } x \text { is rational, }} \\ {0,} & {\text { if } x \text { is irrational. }}\end{array}\right.$$

Нехай$a \in \mathbb{R} .$ Оскільки кожен відкритий інтервал містить як раціональні, так і ірраціональні числа, то для будь-якого$\delta>0$ вибору буде$L \in \mathbb{R},$ існувати$x \in(a-\delta, a+\delta),$$x \neq a,$ таке, що

$$|f(x)-L| \geq \frac{1}{2}.$$

Отже,$\lim _{x \rightarrow a} f(x)$ не існує жодного дійсного числа$a$.

Приклад$\PageIndex{6}$

Визначте$f: \mathbb{R} \rightarrow \mathbb{R}$ по

$$f(x)=\left\{\begin{array}{ll}{x,} & {\text { if } x \text { is rational, }} \\ {0,} & {\text { if } x \text { is irrational. }}\end{array}\right.$$

Тоді$\lim _{x \rightarrow 0} f(x)=0$ з тих пір, дається$\epsilon>0,|f(x)|<\epsilon$ надано$|x|<\epsilon$.

Вправа$\PageIndex{9}$

Показати, що якщо$f$ так, як наведено в попередньому прикладі і$a \neq 0$, то$\lim _{x \rightarrow a} f(x)$ не існує.

Вправа$\PageIndex{11}$

Визначте$f: \mathbb{R} \rightarrow \mathbb{R}$ по

$$f(x)=\left\{\begin{array}{ll}{\frac{1}{q},} & {\text { if } x \text { is rational and } x=\frac{p}{q},} \\ {0,} & {\text { if } x \text { is irrational, }}\end{array}\right.$$

де$p$ і$q$ приймаються відносно прості цілі числа з$q>0,$ і ми приймаємо,$q=1$ коли$x=0 .$ Показати, що, для будь-якого дійсного числа$a, \lim _{x \rightarrow a} f(x)=0$.

Приклад$\PageIndex{7}$

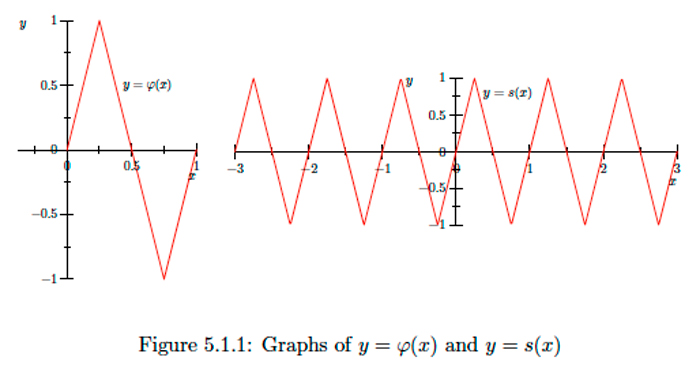
Визначте$\varphi:[0,1] \rightarrow[-1,1]$ по

$$\varphi(x)=\left\{\begin{array}{ll}{4 x,} & {\text { if } 0 \leq x \leq \frac{1}{4},} \\ {2-4 x,} & {\text { if } \frac{1}{4}<x<\frac{3}{4},} \\ {4 x-4,} & {\text { if } \frac{3}{4} \leq x \leq 1.}\end{array}\right.$$

Далі визначаємо$s: \mathbb{R} \rightarrow \mathbb{R}$ по$s(x)=\varphi(x-\lfloor x\rfloor),$ де$\lfloor x\rfloor$ позначає найбільше ціле число менше або рівне$x$ (тобто$\lfloor x\rfloor$ є підлогою$x$). Функція$s$ є прикладом пилоподібної функції. Дивіться графіки$\varphi$ і на$s$ малюнку$5.1 .1 .$ Зверніть увагу, що для будь-якого$n \in \mathbb{Z}$,

$$s([n, n+1])=[-1,1].$$

Тепер давайте$D=\mathbb{R} \backslash\{0\}$ і визначте$\sigma: D \rightarrow \mathbb{R}$ по

$$\sigma(x)=s\left(\frac{1}{x}\right).$$

Див. Графік на$\sigma$ малюнку$5.1 .2 .$ Зверніть увагу, що для будь-якого$n \in \mathbb{Z}^{+}$,

$$\sigma\left(\left[\frac{1}{n+1}, \frac{1}{n}\right]\right)=s([n, n+1])=[-1,1].$$

Значить ні для$\epsilon>0, \sigma((0, \epsilon))=[-1,1],$ кого і так$\lim _{x \rightarrow 0^{+}} \sigma(x)$ не існує. Точно так само$\lim _{x \rightarrow 0^{-}} \sigma(x)$ ні не$\lim _{x \rightarrow 0} \sigma(x)$ існує.

Приклад$\PageIndex{8}$

$s$Дозволяти бути пилоподібною функцією попереднього прикладу і нехай$D=\mathbb{R} \backslash\{0\} .$ Визначити$\psi: D \rightarrow \mathbb{R}$ по

$$\psi(x)=x s\left(\frac{1}{x}\right).$$

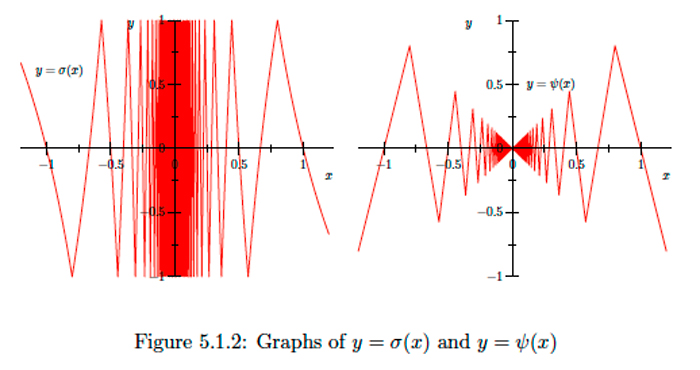
Див. Рисунок 5.1 .2 для графіка$\psi .$ Тоді для всіх$x \in D$,

$$-|x| \leq \psi(x) \leq|x|,$$

і так$\lim _{x \rightarrow 0} \psi(x)=0$ за теоремою стискання.

Визначення

Нехай$D \subset \mathbb{R}$ і$f: D \rightarrow \mathbb{R} .$ Ми говоримо$f$ обмежена, якщо існує дійсне число$B$ таке, що$|f(x)| \leq B$ для всіх$x \in D$.

Вправа$\PageIndex{12}$

$f: \mathbb{R} \rightarrow \mathbb{R}$Припустимо, обмежена. Покажіть, що$\lim _{x \rightarrow 0} x f(x)=0$.