10.5: Використовуйте властивості логарифмів

Цілі навчання

До кінця цього розділу ви зможете:

• Використовуйте властивості логарифмів
• Скористайтеся зміною базової формули

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Оцініть: а.$a^{0}$ б$a^{1}$.
   Якщо ви пропустили цю проблему, перегляньте приклад 5.14.
2. Пишіть з раціональним показником:$\sqrt[3]{x^{2} y}$.
   Якщо ви пропустили цю проблему, перегляньте приклад 8.27.
3. Округлення до трьох знаків після коми:$2.5646415$.
   Якщо ви пропустили цю проблему, перегляньте приклад 1.34.

Використання властивостей логарифмів

Тепер, коли ми дізналися про експоненціальні та логарифмічні функції, ми можемо ввести деякі властивості логарифмів. Це буде дуже корисно, оскільки ми продовжуємо вирішувати як експоненціальні, так і логарифмічні рівняння.

Перші дві властивості походять від визначення логарифмів. Так як$a^{0}=1$, ми можемо перетворити це в логарифмічну форму і отримати$\log _{a} 1=0$. Також, з тих пір$a^{1}=a$, ми отримуємо$\log _{a} a=1$.

Визначення$\PageIndex{1}$

Властивості логарифмів

$\log _{a} 1=0 \quad \log _{a} a=1$

У наступному прикладі ми могли б оцінити логарифм шляхом перетворення в експоненціальну форму, як ми робили раніше, але розпізнавання, а потім застосування властивостей економить час.

Приклад$\PageIndex{1}$

Оцініть за допомогою властивостей логарифмів:

1. $\log _{8} 1$
2. $\log _{6} 6$

Рішення:

а.

$\log _{8} 1$

Користуватися майном,$\log _{a} 1=0$.

$0 \quad \log _{8} 1=0$

б.

$\log _{6} 6$

Користуватися майном,$\log _{a} a=1$.

$1 \quad \log _{6} 6=1$

Вправа$\PageIndex{1}$

Оцініть за допомогою властивостей логарифмів:

1. $\log _{13} 1$
2. $\log _{9} 9$

Відповідь

1. $0$
2. $1$

Вправа$\PageIndex{2}$

Оцініть за допомогою властивостей логарифмів:

1. $\log _{5} 1$
2. $\log _{7} 7$

Відповідь

1. $0$
2. $1$

Наступні два властивості також можна перевірити шляхом перетворення їх з експоненціальної форми в логарифмічну форму, або зворотну.

Експоненціальне рівняння$a^{\log _{a} x}=x$ перетворюється на логарифмічне рівняння$\log _{a} x=\log _{a} x$, яке є істинним твердженням для позитивних значень$x$ лише для.

Логарифмічне рівняння$\log _{a} a^{x}=x$ перетворюється в експоненціальне рівняння$a^{x}=a^{x}$, яке також є істинним твердженням.

Ці дві властивості називаються зворотними властивостями, тому що, коли ми маємо однакову базу, піднімаючи до влади «скасовує» журнал і беручи журнал «скасовує» підвищення до влади. Ці два властивості показують склад функцій. Обидва закінчилися функцією ідентичності, яка знову показує, що експоненціальні та логарифмічні функції є зворотними функціями.

Визначення$\PageIndex{2}$

Обернені властивості логарифмів

Для$a>0, x>0$ і$a \neq 1$,

$a^{\log _{a} x}=x \quad \log _{a} a^{x}=x$

У наступному прикладі застосуємо зворотні властивості логарифмів.

Приклад$\PageIndex{2}$

Оцініть за допомогою властивостей логарифмів:

1. $4^{\log _{4} 9}$
2. $\log _{3} 3^{5}$

Рішення:

а.

$4^{\log _{4} 9}$

Користуватися майном,$a^{\log _{a} x}=x$.

$9 \quad 4^{\log _{4} 9}=9$

б.

$\log _{3} 3^{5}$

Користуватися майном,$a^{\log _{a} x}=x$.

$5 \quad \log _{3} 3^{5}=5$

Вправа$\PageIndex{3}$

Оцініть за допомогою властивостей логарифмів:

1. $5^{\log _{5} 15}$
2. $\log _{7} 7^{4}$

Відповідь

1. $15$
2. $4$

Вправа$\PageIndex{4}$

Оцініть за допомогою властивостей логарифмів:

1. $2^{\log _{2} 8}$
2. $\log _{2} 2^{15}$

Відповідь

1. $8$
2. $15$

Є ще три властивості логарифмів, які стануть в нагоді в нашій роботі. Ми знаємо, що експоненціальні функції та логарифмічна функція дуже взаємопов'язані. Наше визначення логарифма показує нам, що логарифм є показником еквівалентної експоненти. Властивості експонент мають пов'язані властивості для експонент.

У Product Property of Exponents$a^{m} \cdot a^{n}=a^{m+n}$, ми бачимо, що для множення тієї ж бази ми додаємо показники. Product Властивість логарифмів,$\log _{a} M \cdot N=\log _{a} M+\log _{a} N$ говорить нам взяти журнал продукту, ми додаємо журнал факторів.

Визначення$\PageIndex{3}$

Властивість добутку логарифмів

Якщо$M>0, N>0, \mathrm{a}>0$ і$\mathrm{a} \neq 1,$ тоді

$\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N$

Логарифм добутку - це сума логарифмів.

Ми використовуємо цю властивість, щоб записати журнал продукту як суму журналів кожного фактора.

Приклад$\PageIndex{3}$

Використовуйте властивість добутку логарифмів, щоб записати кожен логарифм як суму логарифмів. Спростити, якщо це можливо:

1. $\log _{3} 7 x$
2. $\log _{4} 64 x y$

Рішення:

а.

$\log _{3} 7 x$

Використовуйте властивість продукту,$\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N$.

$\log _{3} 7+\log _{3} x$
$\log _{3} 7 x=\log _{3} 7+\log _{3} x$

б.

$\log _{4} 64 x y$

Використовуйте властивість продукту,$\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N$.

$\log _{4} 64+\log _{4} x+\log _{4} y$

Спростити оцінку,$\log _{4} 64$.

$3+\log _{4} x+\log _{4} y$
$\log _{4} 64 x y=3+\log _{4} x+\log _{4} y$

Вправа$\PageIndex{5}$

Використовуйте властивість добутку логарифмів, щоб записати кожен логарифм як суму логарифмів. Спростити, якщо це можливо:

1. $\log _{3} 3 x$
2. $\log _{2} 8 x y$

Відповідь

1. $1+\log _{3} x$
2. $3+\log _{2} x+\log _{2} y$

Вправа$\PageIndex{6}$

Використовуйте властивість добутку логарифмів, щоб записати кожен логарифм як суму логарифмів. Спростити, якщо це можливо:

1. $\log _{9} 9 x$
2. $\log _{3} 27 x y$

Відповідь

1. $1+\log _{9} x$
2. $3+\log _{3} x+\log _{3} y$

Аналогічно, у частковому властивості експонентів$\frac{a^{m}}{a^{n}}=a^{m-n}$, ми бачимо, що для поділу тієї ж бази ми віднімаємо показники. Коефіцієнтна властивість логарифмів,$\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N$ говорить нам взяти журнал частки, віднімаємо журнал чисельника та знаменника.

Визначення$\PageIndex{4}$

Частна властивість логарифмів

Якщо$M>0, N>0, \mathrm{a}>0$ і$\mathrm{a} \neq 1,$ тоді

$\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N$

Логарифм частки - це різниця логарифмів.

Зауважте, що$\log _{a} M=\log _{a} N \not=\log _{a}(M-N)$.

Ми використовуємо цю властивість, щоб записати журнал частки як різницю журналів кожного фактора.

Приклад$\PageIndex{4}$

Використовуйте Коефіцієнтну властивість логарифмів, щоб записати кожен логарифм як різницю логарифмів. Спрощуйте, якщо це можливо.

1. $\log _{5} \frac{5}{7}$
2. $\log \frac{x}{100}$

Рішення:

а.

$\log _{5} \frac{5}{7}$

Використовуйте властивість частки,$\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N$.

$\log _{5} 5-\log _{5} 7$

Спростити.

$1-\log _{5} 7$

$\log _{5} \frac{5}{7}=1-\log _{5} 7$

б.

$\log \frac{x}{100}$

Використовуйте властивість частки,$\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N$.

$\log x-\log 100$

Спростити.

$\log x-2$

$\log \frac{x}{100}=\log x-2$

Вправа$\PageIndex{7}$

Використовуйте Коефіцієнтну властивість логарифмів, щоб записати кожен логарифм як різницю логарифмів. Спрощуйте, якщо це можливо.

1. $\log _{4} \frac{3}{4}$
2. $\log \frac{x}{1000}$

Відповідь

1. $\log _{4} 3-1$
2. $\log x-3$

Вправа$\PageIndex{8}$

Використовуйте Коефіцієнтну властивість логарифмів, щоб записати кожен логарифм як різницю логарифмів. Спрощуйте, якщо це можливо.

1. $\log _{2} \frac{5}{4}$
2. $\log \frac{10}{y}$

Відповідь

1. $\log _{2} 5-2$
2. $1-\log y$

Третя властивість логарифмів пов'язана з Влада властивості експонентів$\left(a^{m}\right)^{n}=a^{m \cdot n}$, ми бачимо, що, щоб підняти ступінь до степеня, ми множимо показники. Влада властивість логарифмів,$\log _{a} M^{p}=p \log _{a} M$ говорить нам взяти журнал числа, піднятого до степеня, ми множимо потужність на журнал числа.

Визначення$\PageIndex{5}$

Власність потужності логарифмів

Якщо$M>0, \mathrm{a}>0, \mathrm{a} \neq 1$ і$p$ є будь-яким дійсним числом, то

$\log _{a} M^{p}=p \log _{a} M$

Журнал числа, піднятого до потужності як добуток потужності раз журнал числа.

Ми використовуємо цю властивість, щоб записати журнал числа, піднятого до степені, як добуток потужності раз журнал числа. Ми по суті беремо показник і кидаємо його перед логарифмом.

Приклад$\PageIndex{5}$

Використовуйте властивість потужності логарифмів, щоб записати кожен логарифм як добуток логарифмів. Спрощуйте, якщо це можливо.

1. $\log _{5} 4^{3}$
2. $\log x^{10}$

Рішення:

а.

$\log _{5} 4^{3}$

Використовуйте властивість Power,$\log _{a} M^{p}=p \log _{a} M$.

3$\log _{5} 4$

$\log _{5} 4^{3}=3 \log _{5} 4$

б.

$\log x^{10}$

Використовуйте властивість Power,$\log _{a} M^{p}=p \log _{a} M$.

$10\log x$

$\log x^{10}=10 \log x$

Вправа$\PageIndex{9}$

Використовуйте властивість потужності логарифмів, щоб записати кожен логарифм як добуток логарифмів. Спрощуйте, якщо це можливо.

1. $\log _{7} 5^{4}$
2. $\log x^{100}$

Відповідь

1. $4\log _{7} 5$
2. 100$\cdot \log x$

Вправа$\PageIndex{10}$

Використовуйте властивість потужності логарифмів, щоб записати кожен логарифм як добуток логарифмів. Спрощуйте, якщо це можливо.

1. $\log _{2} 3^{7}$
2. $\log x^{20}$

Відповідь

1. $7\log _{2} 3$
2. $20\cdot \log x$

Ми підсумовуємо Властивості логарифмів тут для зручності довідки. Хоча природні логарифми є окремим випадком цих властивостей, часто корисно також показати натуральний логарифм версії кожної властивості.

Властивості логарифмів

Якщо$M>0, \mathrm{a}>0, \mathrm{a} \neq 1$ і$p$ є будь-яким дійсним числом, то

Таблиця 10.4.1

Нерухомість	База$a$	База$e$
	\ (a\) ">$\log _{a} 1=0$	\ (e\) ">$\ln 1=0$
	\ (a\) ">$\log _{a} a=1$	\ (e\) ">$\ln e=1$
Зворотні властивості	\ (a\) ">$a^{\log _{a} x}=x$ $\log _{a} a^{x}=x$	\ (e\) ">$e^{\ln x}=x$ $\ln e^{x}=x$
Властивість добутку логарифмів	\ (a\) ">$\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N$	\ (e\) ">$\ln (M \cdot N)=\ln M+\ln N$
Частна властивість логарифмів	\ (a\) ">$\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N$	\ (e\) ">$\ln \frac{M}{N}=\ln M-\ln N$
Власність потужності логарифмів	\ (a\) ">$\log _{a} M^{p}=p \log _{a} M$	\ (e\) ">$\ln M^{p}=p \ln M$

Тепер, коли у нас є властивості, ми можемо використовувати їх, щоб «розширити» логарифмічний вираз. Це означає записати логарифм у вигляді суми або різниці і без будь-яких повноважень.

Зазвичай ми застосовуємо Product і Quotient Властивості, перш ніж застосовувати Властивість живлення.

Приклад$\PageIndex{6}$

Використовуйте Властивості логарифмів, щоб розширити логарифм$\log _{4}\left(2 x^{3} y^{2}\right)$. Спрощуйте, якщо це можливо.

Рішення:

Використовуйте властивість продукту,$\log _{a} M \cdot N=\log _{a} M+\log _{a} N$.

Використовуйте властивість влади$\log _{a} M^{p}=p \log _{a} M$, на останніх двох термінів. Спростити.

Вправа$\PageIndex{11}$

Використовуйте Властивості логарифмів, щоб розширити логарифм$\log _{2}\left(5 x^{4} y^{2}\right)$. Спрощуйте, якщо це можливо.

Відповідь

$\log _{2} 5+4 \log _{2} x+2 \log _{2} y$

Вправа$\PageIndex{12}$

Використовуйте Властивості логарифмів, щоб розширити логарифм$\log _{3}\left(7 x^{5} y^{3}\right)$. Спрощуйте, якщо це можливо.

Відповідь

$\log _{3} 7+5 \log _{3} x+3 \log _{3} y$

Коли у нас є радикал в логарифмічному виразі, корисно спочатку записати його радиканд як раціональний показник.

Приклад$\PageIndex{7}$

Використовуйте Властивості логарифмів, щоб розширити логарифм$\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}$. Спрощуйте, якщо це можливо.

Рішення

$\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}$

Перепишіть радикал з раціональним показником.

$\log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)^{\frac{1}{4}}$

Використовуйте властивість Power,$\log _{a} M^{p}=p \log _{a} M$.

$\frac{1}{4} \log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)$

Використовуйте властивість частки,$\log _{a} M \cdot N=\log _{a} M-\log _{a} N$.

$\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\log _{2}\left(3 y^{2} z\right)\right)$

Використовуйте Product Property$\log _{a} M \cdot N=\log _{a} M+\log _{a} N$, у другому семестрі.

$\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\left(\log _{2} 3+\log _{2} y^{2}+\log _{2} z\right)\right)$

Використовуйте властивість Power$\log _{a} M^{p}=p \log _{a} M$, всередині дужок.

$\frac{1}{4}\left(3 \log _{2} x-\left(\log _{2} 3+2 \log _{2} y+\log _{2} z\right)\right)$

Спрощення шляхом розподілу.

$\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)$

$\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}=\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)$

Вправа$\PageIndex{13}$

Використовуйте Властивості логарифмів, щоб розширити логарифм$\log _{4} \sqrt[5]{\frac{x^{4}}{2 y^{3} z^{2}}}$. Спрощуйте, якщо це можливо.

Відповідь

$\frac{1}{5}\left(4 \log _{4} x-\frac{1}{2}-3 \log _{4} y-2 \log _{4} z\right)$

Вправа$\PageIndex{14}$

Використовуйте Властивості логарифмів, щоб розширити логарифм$\log _{3} \sqrt[3]{\frac{x^{2}}{5 y z}}$. Спрощуйте, якщо це можливо.

Відповідь

$\frac{1}{3}\left(2 \log _{3} x-\log _{3} 5-\log _{3} y-\log _{3} z\right)$

Протилежність розширенню логарифма полягає в тому, щоб конденсувати суму або різницю логарифмів, які мають однакову основу, в один логарифм. Ми знову використовуємо властивості логарифмів, щоб допомогти нам, але навпаки.

Щоб стиснути логарифмічні вирази з однаковою основою в один логарифм, ми починаємо з використання властивості Power, щоб отримати коефіцієнти термінів журналу, щоб бути одним, а потім Product і Quotient Properties за потребою.

Приклад$\PageIndex{8}$

Використовуйте Властивості логарифмів для згущення логарифма$\log _{4} 3+\log _{4} x-\log _{4} y$. Спрощуйте, якщо це можливо.

Рішення:

Всі вирази журналу мають однакову базу,$4$.

Перші два терміни додаються, тому ми використовуємо Product Property,$\log _{a} M+\log _{a} N=\log _{a} M : N$.

Оскільки журнали віднімаються, ми використовуємо властивість Quotient,$\log _{a} M-\log _{a} N=\log _{a} \frac{M}{N}$.

Вправа$\PageIndex{15}$

Використовуйте Властивості логарифмів для згущення логарифма$\log _{2} 5+\log _{2} x-\log _{2} y$. Спрощуйте, якщо це можливо.

Відповідь

$\log _{2} \frac{5 x}{y}$

Вправа$\PageIndex{16}$

Використовуйте Властивості логарифмів для згущення логарифма$\log _{3} 6-\log _{3} x-\log _{3} y$. Спрощуйте, якщо це можливо.

Відповідь

$\log _{3} \frac{6}{x y}$

Приклад$\PageIndex{9}$

Використовуйте Властивості логарифмів для згущення логарифма$2 \log _{3} x+4 \log _{3}(x+1)$. Спрощуйте, якщо це можливо.

Рішення:

Вирази журналу мають однакову базу,$3$.

$2 \log _{3} x+4 \log _{3}(x+1)$

Використовуйте властивість Power,$\log _{a} M+\log _{a} N=\log _{a} M \cdot N$.

$\log _{3} x^{2}+\log _{3}(x+1)^{4}$

Терміни додаються, тому ми використовуємо Product Property,$\log _{a} M+\log _{a} N=\log _{a} M \cdot N$.

$\log _{3} x^{2}(x+1)^{4}$
$2 \log _{3} x+4 \log _{3}(x+1)=\log _{3} x^{2}(x+1)^{4}$

Вправа$\PageIndex{17}$

Використовуйте Властивості логарифмів для згущення логарифма$3 \log _{2} x+2 \log _{2}(x-1)$. Спрощуйте, якщо це можливо.

Відповідь

$\log _{2} x^{3}(x-1)^{2}$

Вправа$\PageIndex{18}$

Використовуйте Властивості логарифмів для згущення логарифма$2 \log x+2 \log (x+1)$. Спрощуйте, якщо це можливо.

Відповідь

$\log x^{2}(x+1)^{2}$

Використовуйте формулу «Зміна бази»

Щоб оцінити логарифм з будь-якою іншою основою, ми можемо використовувати формулу Change-of-Base. Ми покажемо, як це виводиться.

$\begin{array} {l c} {\text{Suppose we want to evaluate} \log_{a}M} & {\log_{a}M} \\ {\text{Let} \:y =\log_{a}M. }&{y=\log_{a}M} \\ {\text{Rewrite the epression in exponential form. }}&{a^{y}=M } \\ {\text{Take the }\:\log_{b} \text{of each side.}}&{\log_{b}a^{y}=\log_{b}M}\\ {\text{Use the Power Property.}}&{y\log_{b}a=\log_{b}M} \\ {\text{Solve for}\:y. }&{y=\frac{\log_{b}M}{\log_{b}a}} \\ {\text{Substiture}\:y=\log_{a}M.}&{\log_{a}M=\frac{\log_{b}M}{\log_{b}a}} \end{array}$

Формула зміни бази вводить нову базу$b$. Це може бути будь-яка база, яку$b$ ми хочемо де$b>0,b≠1$. Оскільки наші калькулятори мають ключі для логарифмів base$10$ та base$e$, ми перепишемо формулу Change-of-Base з новою базою як$10$ or$e$.

Визначення$\PageIndex{6}$

Формула зміни бази

Для будь-яких логарифмічних основ$a, b$ і$M>0$,

$\begin{array}{lll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}$

Коли ми використовуємо калькулятор, щоб знайти значення логарифма, ми зазвичай округляємо до трьох десяткових знаків. Це дає нам приблизне значення, і тому ми використовуємо приблизно рівний символ$(≈)$.

Приклад$\PageIndex{10}$

Округлення до трьох знаків після коми, приблизне$\log _{4} 35$.

Рішення:

Таблиця 10.4.2

Використовуйте формулу «Зміна бази».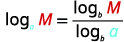
Визначте$a$ і$M$. Вибирайте$10$ для$b$.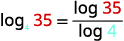
Введіть вираз$\frac{\log 35}{\log 4}$ в калькулятор за допомогою кнопки log для base$10$. Округлення до трьох знаків після коми.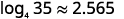

Вправа$\PageIndex{19}$

Округлення до трьох знаків після коми, приблизне$\log _{3} 42$.

Відповідь

$3.402$

Вправа$\PageIndex{20}$

Округлення до трьох знаків після коми, приблизне$\log _{5} 46$.

Відповідь

$2.379$

Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з використанням властивостей логарифмів.

• Використання властивостей логарифмів для розширення журналів
• Використання властивостей логарифмів для ущільнення журналів
• Зміна бази

Ключові концепції

• $\log _{a} 1=0 \quad \log _{a} a=1$
• Обернені властивості логарифмів
  • Для$a>0,x>0$ і$a≠1$

    $a^{\log _{a} x}=x \quad \log _{a} a^{x}=x$

• Властивість добутку логарифмів
  • Якщо$M>0,N>0,a>0$ і$a≠1$, то,

    $\log _{a} M \cdot N=\log _{a} M+\log _{a} N$

    Логарифм добутку - це сума логарифмів.
• Частна властивість логарифмів
  • Якщо$M>0, N>0, \mathrm{a}>0$ і$a≠1$, то,

    $\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N$

    Логарифм частки - це різниця логарифмів.
• Власність потужності логарифмів
  • Якщо$M>0,a>0,a≠1$ і$p$ є будь-яким дійсним числом, то

    $\log _{a} M^{p}=p \log _{a} M$

    Журнал числа, піднятого до потужності, є добутком потужності раз журнал числа.
• Властивості логарифмів Summary
  Якщо$M>0,a>0,a≠1$ і$p$ є будь-яким дійсним числом то,

Таблиця 10.4.1

Нерухомість	База$a$	База$e$
	\ (a\) ">$\log _{a} 1=0$	\ (e\) ">$\ln 1=0$
	\ (a\) ">$\log _{a} a=1$	\ (e\) ">$\ln e=1$
Зворотні властивості	\ (a\) ">$a^{\log _{a} x}=x$ $\log _{a} a^{x}=x$	\ (e\) ">$e^{\ln x}=x$ $\ln e^{x}=x$
Властивість добутку логарифмів	\ (a\) ">$\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N$	\ (e\) ">$\ln (M \cdot N)=\ln M+\ln N$
Частна властивість логарифмів	\ (a\) ">$\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N$	\ (e\) ">$\ln \frac{M}{N}=\ln M-\ln N$
Власність потужності логарифмів	\ (a\) ">$\log _{a} M^{p}=p \log _{a} M$	\ (e\) ">$\ln M^{p}=p \ln M$

• Формула зміни бази
  Для будь-яких логарифмічних основ$a$ і$b$, і$M>0$,

  $\begin{array}{ll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}$