8.9: Використовуйте комплексну систему числення
- Page ID
- 59636
До кінця цього розділу ви зможете:
- Оцінити квадратний корінь від'ємного числа
- Додавання та віднімання комплексних чисел
- Множення комплексних чисел
- Розділити комплексні числа
- Спростіть повноваження\(i\)
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- З огляду на цифри\(-4,-\sqrt{7}, 0 . \overline{5}, \frac{7}{3}, 3, \sqrt{81}\), перерахуйте
- раціональні числа
- ірраціональні числа
- реальні числа
Якщо ви пропустили цю проблему, перегляньте приклад 1.42.
- Помножити:\((x−3)(2x+5)\).
Якщо ви пропустили цю проблему, перегляньте приклад 5.28. - Раціоналізувати знаменник:\(\frac{\sqrt{5}}{\sqrt{5}-\sqrt{3}}\)
Якщо ви пропустили цю проблему, перегляньте приклад 5.32.
Оцінити квадратний корінь від'ємного числа
Всякий раз, коли у нас є квадратний корінь негативного числа, ми говоримо, що немає реального числа, яке дорівнює, що квадратний корінь. Наприклад, для спрощення\(\sqrt{-1}\) шукаємо реальне число\(x\) так, щоб\(x^{2}=-1\). Оскільки всі дійсні числа в квадраті є додатними числами, не існує реального числа, яке дорівнює\(–1\) при квадраті.
Математики часто розширювали свої системи числення за потребою. Вони додали\(0\) до підрахунку чисел, щоб отримати цілі числа. Коли їм потрібні від'ємні залишки, вони додали від'ємні числа, щоб отримати цілі числа. Коли їм потрібно було уявлення про частини цілого, вони додавали дроби і отримали раціональні числа. Додавання ірраціональних чисел дозволено чисел типу\(\sqrt{5}\). Все це разом дало нам реальні цифри, і поки що у вашому вивченні математики цього було достатньо.
Але тепер ми розширимо дійсні числа, щоб включити квадратні корені від'ємних чисел. Почнемо з визначення уявної одиниці\(i\) як числа, квадрат якого є\(–1\).
Визначення\(\PageIndex{1}\)
Уявна одиниця\(i\) - це число, квадрат якого дорівнює\(-1\).
\(i^{2}=-1 \text { or } i=\sqrt{-1}\)
Ми будемо використовувати уявну одиницю для спрощення квадратних коренів від'ємних чисел.
Визначення\(\PageIndex{2}\)
Квадратний корінь від'ємного числа
Якщо\(b\) є додатним дійсним числом, то
\(\sqrt{-b}=\sqrt{b} i\)
Ми будемо використовувати це визначення в наступному прикладі. Будьте обережні, щоб було зрозуміло,\(i\) що не під радикалом. Іноді ви побачите це написане,\(\sqrt{-b}=i \sqrt{b}\) щоб підкреслити\(i\) не під радикалом. Але\(\sqrt{-b}=\sqrt{b} i\) вважається стандартною формою.
Написати кожен вираз з точки зору\(i\) і спростити можна:
- \(\sqrt{-25}\)
- \(\sqrt{-7}\)
- \(\sqrt{-12}\)
Рішення:
а.
\(\sqrt{-25}\)
Використовуйте визначення квадратного кореня від'ємних чисел.
\(\sqrt{25} i\)
Спростити.
\(5i\)
б.
\(\sqrt{-7}\)
Використовуйте визначення квадратного кореня від'ємних чисел.
\(\sqrt{7} i\)
Спростити.
Будьте обережні, щоб було зрозуміло,\(i\) що не під радикальним знаком.
c.
\(\sqrt{-12}\)
Використовуйте визначення квадратного кореня від'ємних чисел.
\(\sqrt{12} i\)
Спростити\(\sqrt{12}\).
\(2 \sqrt{3} i\)
Напишіть кожен вираз з точки зору\(i\) і спростіть, якщо це можливо:
- \(\sqrt{-81}\)
- \(\sqrt{-5}\)
- \(\sqrt{-18}\)
- Відповідь
-
- \(9i\)
- \(\sqrt{5} i\)
- \(3 \sqrt{2} i\)
Напишіть кожен вираз з точки зору\(i\) і спростіть, якщо це можливо:
- \(\sqrt{-36}\)
- \(\sqrt{-3}\)
- \(\sqrt{-27}\)
- Відповідь
-
- \(6i\)
- \(\sqrt{3} i\)
- \(3\sqrt{3} i\)
Тепер, коли ми знайомі з уявним числом\(i\), ми можемо розширити дійсні числа, включивши уявні числа. Комплексна система числення включає дійсні числа і уявні числа. Комплексне число має вигляд\(a+bi\), де\(a, b\) дійсні числа. Ми\(a\) називаємо реальну\(b\) частину і уявну частину.
Визначення\(\PageIndex{3}\)
Комплексне число має вигляд\(a+bi\), де\(a\) і\(b\) є дійсними числами.
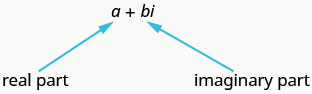
Комплексне число знаходиться в стандартному вигляді, коли пишеться як\(a+bi\), де\(a\) і\(b\) є дійсними числами.
Якщо\(b=0\), то\(a+bi\) стає\(a+0⋅i=a\), і є дійсним числом.
Якщо\(b≠0\), то\(a+bi\) є уявним числом.
Якщо\(a=0\), то\(a+bi\) стає\(0+bi=bi\), і називається чистим уявним числом.
Ми підсумуємо це тут.
| \(a+bi\) | ||
| \(b=0\) |
\(a+0 \cdot i\) \(a\) |
Справжнє число |
| \(b\neq 0\) | \(a+bi\) | уявне число |
| \(a=0\)R |
\(0+bi\) \(bi\) |
Чисте уявне число4 |
Стандартна форма комплексного числа є\(a+bi\), тому це пояснює, чому краща форма - це\(\sqrt{-b}=\sqrt{b} i\) коли\(b>0\).
Діаграма допомагає нам візуалізувати складну систему числення. Він складається як з дійсних чисел, так і уявних чисел.
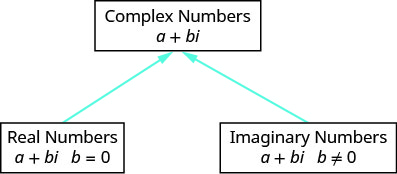
Додавання або віднімання складних чисел
Тепер ми готові виконувати операції додавання, віднімання, множення та ділення на комплексних числах — так само, як ми робили з дійсними числами.
Додавання та віднімання складних чисел дуже схоже на додавання або віднімання подібних термінів. Ми додаємо або віднімаємо реальні частини, а потім додаємо або віднімаємо уявні частини. Наш кінцевий результат повинен бути в стандартному вигляді.
Додати:\(\sqrt{-12}+\sqrt{-27}\).
Рішення:
\(\sqrt{-12}+\sqrt{-27}\)
Використовуйте визначення квадратного кореня від'ємних чисел.
\(\sqrt{12} i+\sqrt{27} i\)
Спростити квадратні коріння.
\(2 \sqrt{3} i+3 \sqrt{3} i\)
Додати.
\(5 \sqrt{3} i\)
Додати:\(\sqrt{-8}+\sqrt{-32}\).
- Відповідь
-
\(6 \sqrt{2} i\)
Додати:\(\sqrt{-27}+\sqrt{-48}\)
- Відповідь
-
\(7 \sqrt{3} i\)
Не забудьте додати як реальні частини, так і уявні частини в наступному прикладі.
Спростити:
- \((4-3 i)+(5+6 i)\)
- \((2-5 i)-(5-2 i)\)
Рішення:
а.
\((4-3 i)+(5+6 i)\)
Використовуйте асоціативну властивість, щоб скласти реальні частини та уявні частини разом.
\((4+5)+(-3 i+6 i)\)
Спростити.
\(9+3i\)
б.
\((2-5 i)-(5-2 i)\)
Розподілити.
\(2-5 i-5+2 i\)
Використовуйте асоціативну властивість, щоб скласти реальні частини та уявні частини разом.
\(2-5-5 i+2 i\)
Спростити.
\(-3-3 i\)
Спростити:
- \((2+7 i)+(4-2 i)\)
- \((8-4 i)-(2-i)\)
- Відповідь
-
- \(6+5i\)
- \(6-3i\)
Спростити:
- \((3-2 i)+(-5-4 i)\)
- \((4+3 i)-(2-6 i)\)
- Відповідь
-
- \(-2-6i\)
- \(2+9i\)
Множення комплексних чисел
Множення комплексних чисел також багато в чому схоже на множення виразів з коефіцієнтами і змінними. Є лише один особливий випадок, який ми повинні розглянути. Ми розглянемо це після практики в наступних двох прикладах.
Помножити:\(2 i(7-5 i)\)
Рішення:
\(2 i(7-5 i)\)
Розподілити.
\(14 i-10 i^{2}\)
Спростити\(i^{2}\).
\(14 i-10(-1)\)
Помножити.
\(14 i+10\)
Пишіть в стандартній формі.
\(10+14i\)
Помножити:\(4 i(5-3 i)\).
- Відповідь
-
\(12+20i\)
Помножити:\(-3 i(2+4 i)\).
- Відповідь
-
\(12-6i\)
У наступному прикладі ми множимо біноміали за допомогою властивості Distributive або FOIL.
Помножити:\((3+2 i)(4-3 i)\).
Рішення:
\((3+2 i)(4-3 i)\)
Використовуйте ФОЛЬГУ.
\(12-9 i+8 i-6 i^{2}\)
Спрощуйте\(i^{2}\) і комбінуйте подібні терміни.
\(12-i-6(-1)\)
Помножити.
\(12-i+6\)
Поєднуйте справжні деталі.
\(18-i\)
Множинні:\((5-3 i)(-1-2 i)\).
- Відповідь
-
\(-11-7i\)
Множинні:\((-4-3 i)(2+i)\).
- Відповідь
-
\(-5-10i\)
У наступному прикладі ми могли б використовувати FOIL або візерунок «Продукт біноміальних квадратів».
Помножити:\((3+2 i)^{2}\)
Рішення:
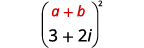 |
|
| Використовуйте візерунок добутку біноміальних квадратів,\((a+b)^{2}=a^{2}+2 a b+b^{2}\). |  |
| Спростити. | 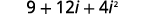 |
| Спростити\(i^{2}\). | 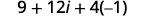 |
| Спростити. | 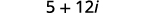 |
Множення за допомогою візерунка Біноміальні квадрати:\((-2-5 i)^{2}\).
- Відповідь
-
\(-21+20 i\)
Множення за допомогою візерунка Біноміальні квадрати:\((-5+4 i)^{2}\).
- Відповідь
-
\(9-40i\)
Оскільки квадратний корінь від'ємного числа не є дійсним числом, ми не можемо використовувати властивість продукту для радикалів. Для того, щоб помножити квадратні корені від'ємних чисел, ми повинні спочатку записати їх як комплексні числа,\(\sqrt{-b}=\sqrt{b}i\) використовуючи.Це одне місце, де студенти схильні робити помилки, тому будьте обережні, коли ви бачите множення з негативним квадратним коренем.
Помножити:\(\sqrt{-36} \cdot \sqrt{-4}\).
Рішення:
Щоб помножити квадратні корені від'ємних чисел, спочатку запишемо їх як комплексні числа.
\(\sqrt{-36} \cdot \sqrt{-4}\)
Запишіть як комплексні числа за допомогою\(\sqrt{-b}=\sqrt{b}i\).
\(\sqrt{36} i \cdot \sqrt{4} i\)
Спростити.
\(6 i \cdot 2 i\)
Помножити.
\(12i^{2}\)
Спростити\(i^{2}\) і примножити.
\(-12\)
Помножити:\(\sqrt{-49} \cdot \sqrt{-4}\).
- Відповідь
-
\(-14\)
Помножити:\(\sqrt{-36} \cdot \sqrt{-81}\).
- Відповідь
-
\(-54\)
У наступному прикладі кожен біном має квадратний корінь від'ємного числа. Перед множенням кожен квадратний корінь від'ємного числа повинен бути записаний як комплексне число.
Помножити:\((3-\sqrt{-12})(5+\sqrt{-27})\).
Рішення:
Щоб помножити квадратні корені від'ємних чисел, спочатку запишемо їх як комплексні числа.
\((3-\sqrt{-12})(5+\sqrt{-27})\)
Запишіть як комплексні числа за допомогою\(\sqrt{-b}=\sqrt{b}i\).
\((3-2 \sqrt{3} i)(5+3 \sqrt{3} i)\)
Використовуйте ФОЛЬГУ.
\(15+9 \sqrt{3} i-10 \sqrt{3} i-6 \cdot 3 i^{2}\)
Поєднуйте подібні терміни і спрощуйте\(i^{2}\).
\(15-\sqrt{3} i-6 \cdot(-3)\)
Множте і комбінуйте як терміни.
\(33-\sqrt{3} i\)
Помножити:\((4-\sqrt{-12})(3-\sqrt{-48})\).
- Відповідь
-
\(-12-22 \sqrt{3} i\)
Помножити:\((-2+\sqrt{-8})(3-\sqrt{-18})\).
- Відповідь
-
\(6+12 \sqrt{2} i\)
Ми вперше розглянули спряжені пари, коли вивчали многочлени. Ми сказали, що пара бічленів, кожен з яких має один і той же перший член і той самий останній член, але один - сума, а один - різниця називається сполученою парою і має форму\((a−b),(a+b)\).
Складна сполучена пара дуже схожа. Для комплексного числа форми\(a+bi\) його сполучений є\(a−bi\). Зверніть увагу, що вони мають однаковий перший член і той самий останній термін, але один - сума, а один - різниця.
Визначення\(\PageIndex{4}\)
Складна сполучена пара має вигляд\(a+bi,a-bi\).
Ми помножимо складну сполучену пару в наступному прикладі.
Помножити:\((3-2 i)(3+2 i)\).
Рішення:
\((3-2 i)(3+2 i)\)
Використовуйте ФОЛЬГУ
\(9+6 i-6 i-4 i^{2}\)
Поєднуйте подібні терміни і спрощуйте\(i^{2}\).
\(9-4(-1)\)
Множте і комбінуйте як терміни.
\(13\)
Помножити:\((4-3 i) \cdot(4+3 i)\).
- Відповідь
-
\(25\)
Помножити:\((-2+5 i) \cdot(-2-5 i)\).
- Відповідь
-
\(29\)
З нашого вивчення многочленів ми знаємо, що добуток кон'югатів завжди\((a-b)(a+b)=a^{2}-b^{2}\) має вигляд. Результат називається різницею квадратів. Ми можемо помножити складну сполучену пару, використовуючи цей візерунок.
Останній приклад ми використовували FOIL. Тепер ми будемо використовувати візерунок «Продукт кон'югатів».
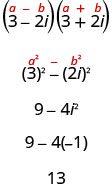
Зверніть увагу, що це той самий результат, який ми знайшли в прикладі 8.8.9.
Коли ми множимо складні кон'югати, добуток останніх членів завжди матиме те\(i^{2}\), що спрощує\(−1\).
\(\begin{array}{c}{(a-b i)(a+b i)} \\ {a^{2}-(b i)^{2}} \\ {a^{2}-b^{2} i^{2}} \\ {a^{2}-b^{2}(-1)} \\ {a^{2}+b^{2}}\end{array}\)
Це призводить нас до добутку складного візерунка кон'югатів:\((a-b i)(a+b i)=a^{2}+b^{2}\)
Визначення\(\PageIndex{5}\)
Добуток складних кон'югатів
Якщо\(a\) і\(b\) є дійсними числами, то
\((a-b i)(a+b i)=a^{2}+b^{2}\)
Множення за допомогою добутку складних кон'югатів візерунка:\((8-2 i)(8+2 i)\).
Рішення:
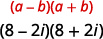 |
|
| Використовуйте твір складного візерунка кон'югатів,\((a-b i)(a+b i)=a^{2}+b^{2}\). | 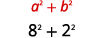 |
| Спростити квадрати. | 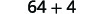 |
| Додати. | 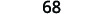 |
Множення за допомогою добутку складних кон'югатів візерунка:\((3-10 i)(3+10 i)\).
- Відповідь
-
\(109\)
Множення за допомогою добутку складних кон'югатів візерунка:\((-5+4 i)(-5-4 i)\).
- Відповідь
-
\(41\)
Розділити комплексні числа
Ділення комплексних чисел багато в чому схоже на раціоналізацію знаменника. Ми хочемо, щоб наш результат був у стандартній формі без уявних чисел у знаменнику.
Розділити:\(\frac{4+3 i}{3-4 i}\).
Рішення:
| Крок 1: Запишіть і чисельник, і знаменник в стандартному вигляді. | Вони обидва в стандартному вигляді. | \(\frac{4+3 i}{3-4 i}\) |
| Крок 2: Помножте чисельник і знаменник на складний сполучений знаменника. | Складний сполучений з\(3-4i\) є\(3+4i\). | \(\frac{(4+3 i)\color{red}{(3+4 i)}}{(3-4 i)\color{red}{(3+4 i)}}\) |
| Крок 3: Спростити і записати результат в стандартному вигляді. |
Використовуйте візерунок\((a-b i)(a+b i)=a^{2}+b^{2}\) в знаменнику. Поєднуйте подібні терміни. Спростити. Напишіть результат в стандартному вигляді. |
\(\begin{array}{c}{\frac{12+16 i+9 i+12 i^{2}}{9+16}} \\ {\frac{12+25 i-12}{25}} \\ {\frac{25 i}{25}} \\ {i}\end{array}\) |
Розділити:\(\frac{2+5 i}{5-2 i}\).
- Відповідь
-
\(i\)
Розділити:\(\frac{1+6 i}{6-i}\).
- Відповідь
-
\(i\)
Ми підсумовуємо кроки тут.
Як розділити комплексні числа
- Пишіть і чисельник, і знаменник в стандартному вигляді.
- Помножте і чисельник, і знаменник на комплексний сполучений знаменника.
- Спростити і написати результат в стандартному вигляді.
Ділимо, написавши відповіді в стандартній формі:\(\frac{-3}{5+2 i}\).
Рішення:
\(\frac{-3}{5+2 i}\)
Помножте чисельник і знаменник на складний сполучений знаменника.
\(\frac{-3(5-2 i)}{(5+2 i)(5-2 i)}\)
Помножте на чисельник і використовуйте добуток складних сполучених візерунків у знаменнику.
\(\frac{-15+6 i}{5^{2}+2^{2}}\)
Спростити.
\(\frac{-15+6 i}{29}\)
Пишіть в стандартній формі.
\(-\frac{15}{29}+\frac{6}{29} i\)
Ділимо, написавши відповідь в стандартній формі:\(\frac{4}{1-4 i}\).
- Відповідь
-
\(\frac{4}{17}+\frac{16}{17} i\)
Ділимо, написавши відповідь в стандартній формі:\(\frac{-2}{-1+2 i}\).
- Відповідь
-
\(\frac{2}{5}+\frac{4}{5} i\)
Будьте обережні, оскільки знайдете сполучений знаменник.
Розділити:\(\frac{5+3 i}{4 i}\).
Рішення:
\(\frac{5+3 i}{4 i}\)
Напишіть знаменник в стандартному вигляді.
\(\frac{5+3 i}{0+4 i}\)
Помножте чисельник і знаменник на складний сполучений знаменника.
\(\frac{(5+3 i)(0-4 i)}{(0+4 i)(0-4 i)}\)
Спростити.
\(\frac{(5+3 i)(-4 i)}{(4 i)(-4 i)}\)
Помножити.
\(\frac{-20 i-12 i^{2}}{-16 i^{2}}\).
Спростити\(i^{2}\).
\(\frac{-20 i+12}{16}\)
Рерайт в стандартному вигляді.
\(\frac{12}{16}-\frac{20}{16} i\)
Спрощення дробів.
\(\frac{3}{4}-\frac{5}{4} i\)
Розділити:\(\frac{3+3 i}{2 i}\).
- Відповідь
-
\(\frac{3}{2}-\frac{3}{2} i\)
Розділити:\(\frac{2+4 i}{5 i}\).
- Відповідь
-
\(\frac{4}{5}-\frac{2}{5} i\)
Спростити повноваження\(i\)
Повноваження\(i\) зробити цікавий шаблон, який допоможе нам спростити вищі сили\(i\). Давайте оцінимо повноваження,\(i\) щоб побачити закономірність.
\(\begin{array}{ccc}{i^{1}} & {i^{2}} & {i^{3}} & {i^{4}} \\ {i} & {-1} & {i^{2}\cdot i} & {i^{2}\cdot i^{2}}\\ {}&{}&{-1\cdot i}&{(-1)(-1)}\\ {}&{}&{-i}&{1}\end{array}\)
\(\begin{array}{cccc}{i^{5}} & {i^{6}} & {i^{7}} & {i^{8}} \\ {i^{4} \cdot i} & {i^{4} \cdot i^{2}} & {i^{4} \cdot i^{3}} & {i^{4} \cdot i^{4}} \\ {1 \cdot i} & {1 \cdot i^{2}} & {1 \cdot i^{3}} & {1 \cdot 1} \\ {i} & {i^{2}} & {i^{3}} & {1} \\ {}&{-1} & {-i}\end{array}\)
Підсумовуємо це зараз.
\(\begin{array}{ll}{i^{1}=i} & {i^{5}=i} \\ {i^{2}=-1} & {i^{6}=-1} \\ {i^{3}=-i} & {i^{7}=-i} \\ {i^{4}=1} & {i^{8}=1}\end{array}\)
Якби ми продовжили, візерунок продовжував би повторюватися в блоках по чотири. Ми можемо використовувати цей шаблон, щоб допомогти нам спростити повноваження\(i\). Так як\(i^{4}=1\), ми переписуємо кожну владу\(i^{n}\), як продукт, використовуючи\(i^{4}\) на владу і іншу силу\(i\).
Ми перепишемо його у формі\(i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}\), де показник\(q\), - частка\(n\) ділиться на\(4\) і показник\(r\), є залишком від цього ділення. Наприклад, для спрощення\(i^{57}\) ділимо\(57\) на\(4\) і отримуємо\(14\) з залишком\(1\). Іншими словами,\(57=4⋅14+1\). Так ми пишемо,\(i^{57}=\left(1^{4}\right)^{14} \cdot i^{1}\) а потім спростити звідти.
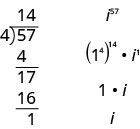
Спростити:\(i^{86}\).
Рішення:
\(i^{86}\)
Розділіть\(86\) на\(4\) і перепишіть\(i^{86}\) в\(i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}\) форму.
\(\left(1^{4}\right)^{21} \cdot i^{2}\)
Спростити.
\((1)^{21} \cdot(-1)\)
Спростити.
\(-1\)
Спростити:\(i^{74}\).
- Відповідь
-
\(-1\)
Спростити:\(i^{92}\).
- Відповідь
-
\(1\)
Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики за допомогою складної системи числення.
- Висловлення квадратних коренів від'ємних чисел за допомогою i
- Віднімання та множення комплексних чисел
- Ділення комплексних чисел
- Переписування повноважень i
Ключові концепції
- Квадратний корінь від'ємного числа
- Якщо\(b\) є додатним дійсним числом, то\ (\ sqrt {-b} =\ sqrt {b} i\
| \(a+bi\) | ||
| \(b=0\) |
\(a+0\cdot i\) \(a\) |
Справжнє число |
| \(b\neq 0\) | \(a+bi\) | уявне число |
| \(a=0\) |
\(0+bi\) \(bi\) |
Чисте уявне число |
-
- Комплексне число знаходиться в стандартній формі, коли записано як a + bi, де a, b - дійсні числа.
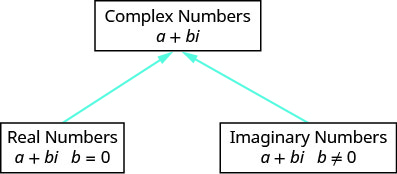
Малюнок 8.8.2
- Комплексне число знаходиться в стандартній формі, коли записано як a + bi, де a, b - дійсні числа.
- Добуток складних кон'югатів
- Якщо\(a, b\) дійсні числа, то
\((a−bi)(a+bi)=a^{2}+b^{2}\)
- Якщо\(a, b\) дійсні числа, то
- Як розділити комплексні числа
- Пишіть і чисельник, і знаменник в стандартному вигляді.
- Помножте чисельник і знаменник на складний сполучений знаменника.
- Спростити і написати результат в стандартному вигляді.
Глосарій
- складна сполучена пара
- Складна сполучена пара має вигляд\(a+bi, a-bi\).
- комплексне число
- Комплексне число має вигляд\(a+bi\), де\(a\) і\(b\) є дійсними числами. Ми\(a\) називаємо реальну\(b\) частину і уявну частину.
- комплексна система числення
- Комплексна система числення складається як з дійсних чисел, так і з уявних чисел.
- уявна одиниця
- Уявна одиниця\(i\) - це число, квадрат якого дорівнює\(–1\). \(i^{2}=-1\)або\(i=\sqrt{−1}\).
- стандартна форма
- Комплексне число знаходиться в стандартному вигляді, коли пишеться як\(a+bi\), де\(a, b\) дійсні числа.
