Skip to main content
LibreTexts - Ukrayinska

1.6: Факторингові поліноми

  1. Last updated
  2. Save as PDF
  • Page ID
    59596

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    У цьому розділі студенти будуть:

    • Фактор найбільший загальний фактор многочлена.
    • Фактор тріпомінал.
    • Фактор за групуванням.
    • Фактор ідеальний квадратний триноміал.
    • Фактор різниці квадратів.
    • Фактор суми та різниці кубів.
    • Факторні вирази з використанням дробових або негативних показників.

    Уявіть, що ми намагаємося знайти площу газону, щоб ми могли визначити, скільки насіння трави придбати. Газон - це зелена частина на рис\(\PageIndex{1}\).

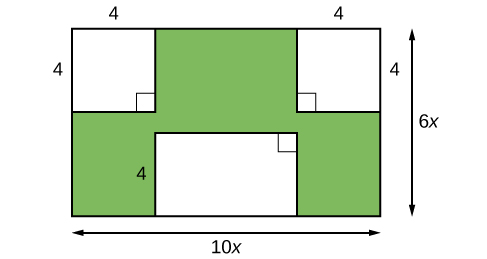
    Великий прямокутник з меншими квадратами і прямокутником всередині. Довжина зовнішнього прямокутника становить 6x, а ширина - 10x. Довжина сторони квадратів дорівнює 4, а висота ширини внутрішнього прямокутника - 4.
    Малюнок\(\PageIndex{1}\)

    Площа всієї області можна знайти за допомогою формули для площі прямокутника.

    \[\begin{align*} A &= lw\\ &= 10x\times6x\\ &= 60x^2\; units^2 \end{align*}\]

    Ділянки ділянок, які не потребують насіння трави, потрібно відняти від площі всього регіону. У двох квадратних областях кожна має площу\(A =s^2=4^2= 16\; units^2\). Інша прямокутна область має одну сторону довжини\(10x−8\) і одну сторону довжини\(4\), що дає площу

    \[A =lw=4(10x−8)=40x−32\; \text{units}^2. \nonumber\]

    Отже, регіон, який потрібно відняти, має площу

    \[2(16)+40x−32= 40x\; \text{units}^2. \nonumber\]

    Територія регіону, яка потребує насіння трави, знаходять шляхом віднімання\(60x^2−40x\; \text{units}^2\). Ця область також може бути виражена в факторованій формі як\(20x (3x−2)\; \text{units}^2\). Ми можемо підтвердити, що це еквівалентний вираз множенням.

    Багато поліноміальні вирази можуть бути записані в простіших формах шляхом факторингу. У цьому розділі ми розглянемо різноманітні методи, які можуть бути використані для множення поліноміальних виразів.

    Факторинг найбільшого спільного фактора многочлена

    Коли ми вивчаємо дроби, то дізнаємося, що найбільший спільний фактор (ГКФ) двох чисел - це найбільше число, яке ділиться рівномірно на обидва числа. Наприклад,\(4\) є GCF\(16\) і\(20\) тому, що це найбільше число, яке ділиться рівномірно на обидва,\(16\) і\(20\) GCF поліномів працює однаково:\(4x\) є GCF\(16x\) і\(20x^2\) тому, що це найбільший многочлен, який ділиться рівномірно в обидва\(16x\) і\(20x^2\).

    При факторингу поліноміального виразу нашим першим кроком має бути перевірка GCF. Шукайте GCF коефіцієнтів, а потім шукайте GCF змінних.

    Визначення: Найбільший спільний фактор

    Найбільшим загальним фактором (ГКФ) многочленів є найбільший многочлен, який ділиться рівномірно на многочлени.

    Howto: Враховуючи поліноміальний вираз, перерахуйте найбільший загальний фактор
    1. Визначте GCF коефіцієнтів.
    2. Визначте GCF змінних.
    3. Об'єднайте, щоб знайти GCF виразу.
    4. Визначте, на що потрібно помножити GCF, щоб отримати кожен член у виразі.
    5. Запишіть факторний вираз як добуток GCF і суму членів, на які нам потрібно помножити.
    Приклад\(\PageIndex{1}\): Factoring the Greatest Common Factor

    Фактор\(6x^3y^3 +45x^2y^2+21xy\).

    Рішення

    Спочатку знайдіть GCF виразу. ЗКФ\(6\)\(45\), і\(21\) є\(3\). ЗКФ\(x^3\)\(x^2\), і\(x\) є\(x\). (Зауважте, що GCF набору виразів у формі завжди\(x^n\) буде показником найнижчого ступеня.) І GCF\(y^3\)\(y^2\), і\(y\) є\(y\). Об'єднайте їх, щоб знайти GCF многочлена,\(3xy\).

    Далі визначте, на що ГКФ потрібно помножити, щоб отримати кожен член многочлена. Ми знаходимо, що

    • \(3xy(2x^2y^2)=6x^3y^3\),
    • \(3xy(15xy)=45x^2y^2\), і
    • \(3xy(7)=21xy\).

    Нарешті, запишіть факторний вираз як добуток GCF і суму термінів, на які нам потрібно помножити.

    \[(3xy)(2x^2y^2+15xy+7) \nonumber\]

    Аналіз

    Після факторингу ми можемо перевірити нашу роботу шляхом множення. Використовуйте розподільну властивість, щоб підтвердити це

    \[(3xy)(2x^2y^2+15xy+7)=6x^3y^3+45x^2y^2+21xy \nonumber\]

    Вправа\(\PageIndex{1}\)

    Фактор\(x(b^2−a)+6(b^2−a)\) шляхом витягування ГКФ.

    Відповідь

    \((b^2−a)(x+6)\)

    Факторинг триноміала з провідним коефіцієнтом 1

    Хоча ми завжди повинні починати з пошуку GCF, витягування GCF - це не єдиний спосіб, яким можуть бути враховані поліноміальні вирази. Многочлен\(x^2+5x+6\) має GCF\(1\), але його можна записати як добуток факторів\((x+2)\) і\((x+3)\).

    Триноми виду\(x^2+bx+c\) можуть бути враховані шляхом знаходження двох чисел з добутком\(c\) і сумою\(b\). Наприклад\(x^2+10x+16\), тріноміал може бути врахований за допомогою чисел\(2\) і\(8\) тому, що добуток цих чисел є\(16\) і їх сума є\(10\). Триноміал може бути переписаний як твір\((x+2)\) і\((x+8)\).

    ФАКТОРИНГ ТРИНОМІАЛЯ З ПРОВІДНИМ КОЕФІЦІЄНТОМ\(1\)

    Триноміал форми\(x^2+bx+c\) може бути записаний у факторованій формі як\((x+p)(x+q)\) де\(pq=c\) і\(p+q=b\).

    Питання і відповіді: Чи може кожен триноміал бути врахований як добуток біноміалів?

    Ні. Деякі многочлени не можуть бути враховані. Ці многочлени, як кажуть, є простими.

    Howto: Дано триноміал у формі\(x^2+bx+c\), factor it
    1. Перелік факторів\(c\).
    2. Знайти\(p\) і\(q\), пару множників\(c\) з сумою\(b\).
    3. Напишіть факторний вираз\((x+p)(x+q)\).
    Приклад\(\PageIndex{2}\): Factoring a Trinomial with Leading Coefficient 1

    Фактор\(x^2+2x−15\).

    Рішення

    У нас є триноміал з провідним коефіцієнтом\(1\)\(b=2\), і\(c=−15\). Нам потрібно знайти два числа з добутком\(−15\) і сумою\(2\). У таблиці перераховуємо фактори\(\PageIndex{1}\), поки не знайдемо пару з потрібною сумою.

    Таблиця\(\PageIndex{1}\)
    Фактори −15 Сума множників
    1, −15 −14
    −1,15 14
    3, −5 −2
    −3,5  

    Тепер, коли ми визначили\(p\)\(−3\) і\(q\) як і\(5\), напишіть факторну форму як\((x−3)(x+5)\).

    Аналіз

    Ми можемо перевірити свою роботу шляхом множення. Використовуйте FOIL, щоб підтвердити це\((x−3)(x+5)=x^2+2x−15\).

    Питання і відповіді: Чи має значення порядок факторів?

    Ні. Множення є комутативним, тому порядок факторів значення не має.

    Вправа\(\PageIndex{2}\)

    Фактор\(x^2−7x+6\).

    Відповідь

    \((x−6)(x−1)\)

    Факторинг за групуванням

    Триноми з провідними коефіцієнтами,\(1\) відмінними від, трохи складніше для фактора. Для цих тріноміалів ми можемо множник, групуючи, розділивши термін x на суму двох членів, факторинг кожної частини виразу окремо, а потім факторинг GCF всього виразу. Триноміал\(2x^2+5x+3\) можна переписати як\((2x+3)(x+1)\) за допомогою цього процесу. Ми починаємо з переписування вихідного виразу,\(2x^2+2x+3x+3\) а потім коефіцієнт кожної частини виразу для отримання\(2x(x+1)+3(x+1)\). Потім ми витягуємо GCF,\((x+1)\) щоб знайти факторний вираз.

    Фактор за групуванням

    Для множення триноміала у вигляді\(ax^2+bx+c\) шляхом групування знаходимо два числа з добутком\(ac\) і сумою\(b\). Ми використовуємо ці числа, щоб розділити\(x\) термін на суму двох членів і множник кожної частини виразу окремо, потім перерахуємо GCF всього виразу.

    Howto: Дано триноміал у формі\(ax^2+bx+c\), factor by grouping.
    1. Перелік факторів\(ac\).
    2. Знайти\(p\) і\(q\), пару множників\(ac\) з сумою\(b\).
    3. Перепишіть оригінальний вираз як\(ax^2+px+qx+c\).
    4. Витягніть ГКФ з\(ax^2+px\).
    5. Витягніть ГКФ з\(qx+c\).
    6. Фактор з GCF виразу.
    Приклад\(\PageIndex{3}\): Factoring a Trinomial by Grouping

    Фактор\(5x^2+7x−6\) за групуванням.

    Рішення

    У нас є триноміал з\(a=5\)\(b=7\), і\(c=−6\). Для початку визначитеся\(ac=−30\). Нам потрібно знайти два числа з добутком\(−30\) і сумою\(7\). У таблиці нижче перерахуємо фактори, поки не знайдемо пару з потрібною сумою.

    Таблиця\(\PageIndex{2}\)
    Фактори −30 Сума множників
    1, −30 −29
    −1,30 29
    2, −15 −13
    −2,15 13
    3, −10 −7
    −3,10 7

    Так\(p=−3\) і\(q=10\).

    \(5x^2−3x+10x−6\)Перепишіть оригінальний вираз як\(ax^2+px+qx+c\).

    \(x(5x−3)+2(5x−3)\)Фактор GCF кожної частини

    \((5x−3)(x+2)\)Фактор з GCF виразу.

    Аналіз

    Ми можемо перевірити свою роботу шляхом множення. Використовуйте FOIL, щоб підтвердити це\((5x−3)(x+2)=5x^2+7x−6\).

    Вправа\(\PageIndex{3}\)

    Фактор:

    1. \(2x^2+9x+9\)
    2. \(6x^2+x−1\)
    Відповідь на

    \((2x+3)(x+3)\)

    Відповідь б

    \((3x-1)(2x+1)\)

    Факторинг ідеального квадратного триноміалу

    Ідеальний квадратний тріноміал - це триноміал, який можна записати як квадрат двочлена. Нагадаємо, що коли біноміал знаходиться в квадраті, результатом є квадрат першого члена, доданий до подвоєного добутку двох членів і квадрату останнього члена.

    \[a^2+2ab+b^2={(a+b)}^2\]

    і

    \[a^2-2ab+b^2={(a-b)}^2\]

    Ми можемо використовувати це рівняння для фактора будь-якого ідеального квадратного триноміала.

    Ідеальні квадратні триноміали

    Ідеальний квадратний триноміал можна записати як квадрат двочлена:

    \[a^2+2ab+b^2=(a+b)^2\]

    Howto: Враховуючи досконалий квадратний тріноміал, введіть його на квадрат біноміального
    1. Підтвердьте, що перший і останній член є ідеальними квадратами.
    2. Підтвердьте, що середній термін вдвічі перевищує добуток\(ab\).
    3. Напишіть факторовану форму як\({(a+b)}^2\).
    Приклад\(\PageIndex{4}\): Factoring a Perfect Square Trinomial

    Фактор\(25x^2+20x+4\).

    Рішення

    Зверніть увагу, що\(25x^2\) і\(4\) є ідеальними квадратами, тому що\(25x^2={(5x)}^2\) і\(4=2^2\). Потім перевірте, чи середній термін вдвічі перевищує добуток\(5x\) і\(2\). Середній термін, дійсно, вдвічі перевищує продукт:\(2(5x)(2)=20x\). Тому триноміал є ідеальним квадратним тріноміалом і може бути записаний як\({(5x+2)}^2\).

    Вправа\(\PageIndex{4}\)

    Фактор\(49x^2−14x+1\).

    Відповідь

    \({(7x−1)}^2\)

    Факторинг різниці квадратів

    Різниця квадратів - це ідеальний квадрат, віднімається від ідеального квадрата. Нагадаємо, що різницю квадратів можна переписати як фактори, що містять однакові терміни, але протилежні знаки, оскільки середні члени скасовують один одного, коли два множники множаться.

    \[a^2−b^2=(a+b)(a−b)\]

    Ми можемо використовувати це рівняння для коефіцієнта будь-яких відмінностей квадратів.

    Відмінності квадратів

    Різницю квадратів можна переписати як два фактори, що містять однакові члени, але протилежні знаки.

    \[a^2−b^2=(a+b)(a−b)\]

    Howto: Враховуючи різницю квадратів, перерахуйте її на біноміали
    1. Підтвердьте, що перший і останній член є ідеальними квадратами.
    2. Напишіть факторовану форму як\((a+b)(a−b)\).
    Приклад\(\PageIndex{5}\): Factoring a Difference of Squares

    Фактор\(9x^2−25\).

    Рішення

    Зверніть увагу, що\(9x^2\) і\(25\) є ідеальними квадратами, тому що\(9x^2={(3x)}^2\) і\(25=5^2\). Многочлен являє собою різницю квадратів і може бути переписаний як\((3x+5)(3x−5)\).

    Вправа\(\PageIndex{5}\)

    Фактор\(81y^2−100\).

    Відповідь

    \((9y+10)(9y−10)\)

    Q&A: Чи існує формула для множення суми квадратів?

    Ні. Сума квадратів не може бути врахована.

    Факторинг суми та різниці кубів

    Тепер ми розглянемо два нових спеціальних продукту: суму і різницю кубиків. Хоча сума квадратів не може бути врахована, сума кубів може бути врахована в біноміальну і триноміальну.

    \[a^3+b^3=(a+b)(a^2−ab+b^2)\]

    Аналогічно сума кубів може бути врахована в біноміал і триноміал, але з різними знаками.

    \[a^3−b^3=(a−b)(a^2+ab+b^2)\]

    Ми можемо використовувати акронім SOAP для запам'ятовування знаків при факторингу суми або різниці кубів. Перша буква кожного слова відноситься до знаків: Те саме Протилежне Завжди Позитивне. Для прикладу розглянемо наступний приклад.

    \[x^3−2^3=(x−2)(x^2+2x+4)\]

    Знак перших 2 такий же, як і знак між\(x^3−2^3\). Знак\(2x\) терміна протилежний знаку між\(x^3−2^3\). І ознака останнього терміну\(4\), завжди позитивний.

    Сума і різниця кубів

    Ми можемо перерахувати суму двох кубів як

    \[a^3+b^3=(a+b)(a^2−ab+b^2)\]

    Ми можемо врахувати різницю двох кубів як

    \[a^3−b^3=(a−b)(a^2+ab+b^2)\]

    Howto: З урахуванням суми кубів або різниці кубів, коефіцієнт його
    1. Підтвердьте, що перший і останній термін - це кубики,\(a^3+b^3\) або\(a^3−b^3\).
    2. Для суми кубиків запишіть факторну форму як\((a+b)(a^2−ab+b^2)\). Для різниці кубиків напишіть факторну форму як\((a−b)(a^2+ab+b^2)\).
    Приклад\(\PageIndex{6}\): Factoring a Sum of Cubes

    Фактор\(x^3+512\).

    Рішення

    Зверніть увагу, що\(x^3\) і\(512\) кубики тому що\(8^3=512\). Перепишіть суму кубів як\((x+8)(x^2−8x+64)\).

    Аналіз

    Після написання суми кубів таким чином, ми могли б подумати, що ми повинні перевірити, чи може триноміальна частина бути врахована далі. Однак тріноміальна частина не може бути врахована, тому нам не потрібно перевіряти.

    Вправа\(\PageIndex{6}\)

    Коефіцієнт суми кубів:\(216a^3+b^3\).

    Відповідь

    \((6a+b)(36a^2−6ab+b^2)\)

    Приклад\(\PageIndex{7}\): Factoring a Difference of Cubes

    Фактор\(8x^3−125\).

    Рішення

    Зверніть увагу, що\(8x^3\) і\(125\) є кубики, тому що\(8x^3={(2x)}^3\) і\(125=5^3\). Запишіть різницю кубиків як\((2x−5)(4x^2+10x+25)\).

    Аналіз

    Так само, як і з сумою кубів, ми не зможемо додатково перерахувати тріноміальну частину.

    Вправа\(\PageIndex{7}\)

    Фактор різниці кубів:\(1000x^3−1\)

    Відповідь

    \((10x−1)(100x^2+10x+1)\)

    Факторингові вирази з дробовими або негативними показниками

    Вирази з дробовими або негативними показниками можуть бути враховані шляхом витягування GCF. Шукайте змінну або показник, який є загальним для кожного члена виразу, і витягніть цю змінну або експоненту, підняту до найнижчої потужності. Ці вирази відповідають тим самим правилам факторингу, що і ті з цілими показниками. Наприклад,\(2x^{\tfrac{1}{4}}+5x^{\tfrac{3}{4}}\) можна врахувати, витягнувши\(x^{\tfrac{1}{4}}\) та переписуючи як\(x^{\tfrac{1}{4}}(2+5x^{\tfrac{1}{2}})\).

    Приклад\(\PageIndex{8}\): Factoring an Expression with Fractional or Negative Exponents

    Фактор\(3x{(x+2)}^{-\tfrac{1}{3}}+4{(x+2)}^{\tfrac{2}{3}}\).

    Рішення

    Фактор з терміном з найменшим значенням показника. У цьому випадку, що б\({(x+2)}^{-\tfrac{1}{3}}\).

    \[\begin{align*} &(x+2)^{-\tfrac{1}{3}}(3x+4(x+2))\qquad \text{Factor out the GCF }\\ &(x+2)^{-\tfrac{1}{3}}(3x+4x+8)\qquad \text{Simplify } \\ &(x+2)^{-\tfrac{1}{3}}(7x+8) \end{align*}\]

    Вправа\(\PageIndex{8}\)

    Фактор\(2{(5a−1)}^{\tfrac{3}{4}}+7a{(5a−1)}^{−\tfrac{1}{4}}\).

    Відповідь

    \({(5a−1)}^{−\tfrac{1}{4}}(17a−2)\)

    Медіа

    Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з факторинговими поліномами.

    1. Визначте GCF

    2. Фактор Триноміали, коли дорівнює 1

    3. Фактор триноми, коли a не дорівнює 1

    4. Факторна сума або різниця кубів

    Ключові рівняння

    різниця квадратів \(a^2−b^2=(a+b)(a−b)\)
    ідеальний квадратний триноміал \(a^2+2ab+b^2=(a+b)^2\)
    сума кубів \(a^3+b^3=(a+b)(a^2−ab+b^2)\)
    різниця кубиків \(a^3−b^3=(a−b)(a^2+ab+b^2)\)
    • Найбільший загальний фактор, або GCF, може бути врахований з полінома. Перевірка GCF повинна бути першим кроком у будь-якій проблемі факторингу. Див. Приклад.
    • Триноми з провідним коефіцієнтом 1 можуть бути враховані шляхом знаходження чисел, які мають добуток третього члена і суму другого члена. Див. Приклад.
    • Триноми можуть бути враховані за допомогою процесу, який називається факторингом шляхом групування. Див. Приклад.
    • Ідеальні квадратні триноми та різниця квадратів є спеціальними виробами і можуть бути враховані за допомогою рівнянь. Див. приклад і приклад.
    • Суму кубів і різницю кубів можна врахувати за допомогою рівнянь. Див. приклад і приклад.
    • Поліноми, що містять дробові та негативні показники, можуть бути враховані шляхом витягування GCF. Див. Приклад.